A magnetic field B exists between OA and OB. Inclined at an angle (θ), a charged particle strikes at point A on surface OA, at a distance (2Kcos(θ))(qvB) from O, where K is kinetic energy, q is the charge and v is the velocity of the particle. At what angle with horizontal (measured from end B) will the charged particle emerge from OB?

θ
90∘−θ
90∘+θ
90∘
The correct Answer is:D
r=mvqB=2KqvB
Thus, OA=rcosθ(given)
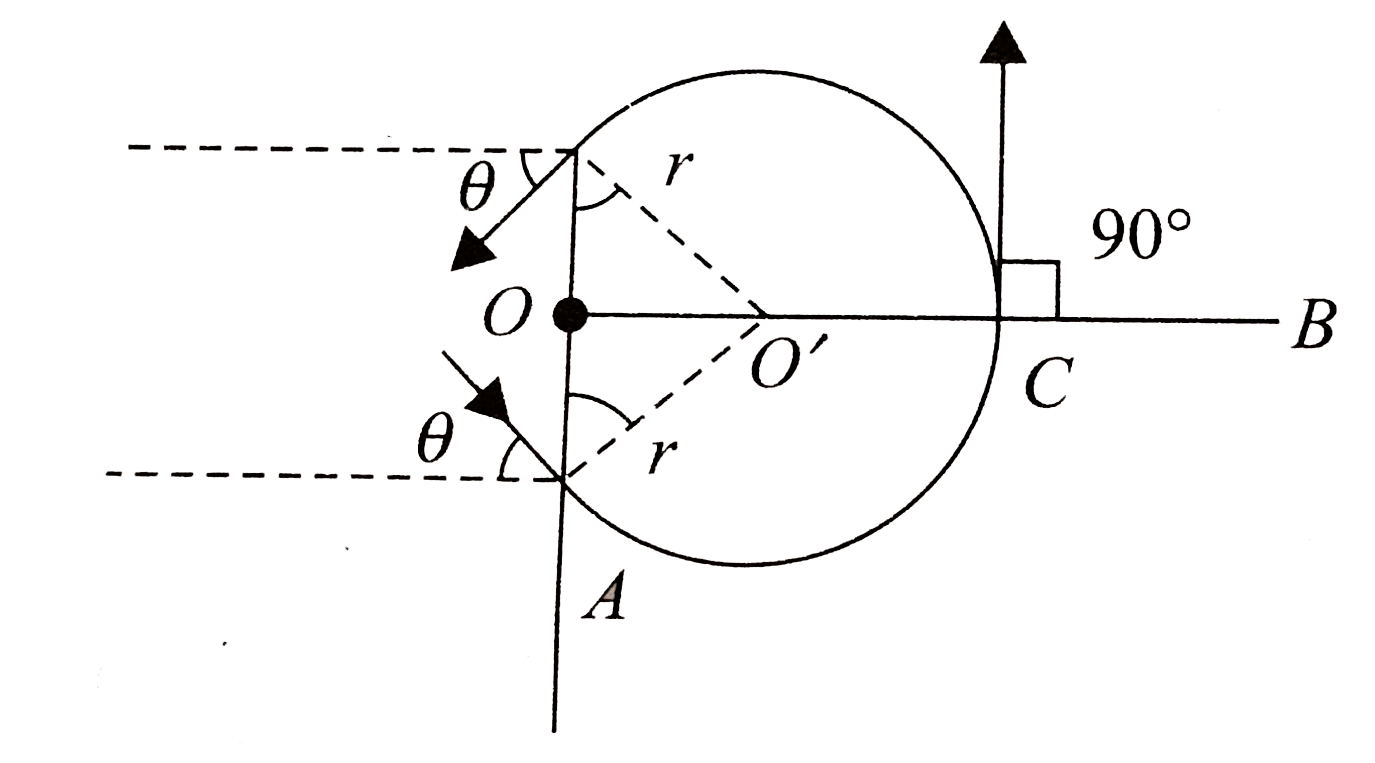
On line OB, centre O' of part of circle (in which particle moves) lies. The tangent at C with OB makes an angle of 90∘. Particle leaves circular path at C. thus, required angle 90∘.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- Moving charges and magnetismBOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank
20 Videos
Similar Questions
A paricle is projected at an anged θ from the horizontal with kinetic energy (T). What is the kinetic energy of the particle at the highest point ?
View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View Solution
Knowledge Check
AB and AC are boundary lines within which a magnetic field B exists. If the magnetic field is absent, a charged particle of mass m and charge q must have passed through a point P on angle bisector of -BAC, at a distance r(√2) from A, if it has fallen on AB normally at a point Q such that QP =r. If the magnetic field is present, how much time the charged particle will take to come out of the magnetic field
 AmπBqB2mπBqC4mπBqDmπ2Bq
AmπBqB2mπBqC4mπBqDmπ2BqA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
AgcosθθvBgvsinθCgvθDgθvsinθA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2r22mCEq2m2t2DEqm2t
A particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA charged particle q is moving in the presence of a magnetic field B which is inclined to an angle 30° with the direction of the motion of the particle. Draw the trajectory followed by the particle in the presence of the field and explain how the particle describes this path.
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View SolutionA positive charge q is projected in magnetic field of width mv√2qB with velocity v . Then, the time taken by charged particle to emerge from the magnetic field is
View Solution