AB and AC are boundary lines within which a magnetic field B exists. If the magnetic field is absent, a charged particle of mass m and charge q must have passed through a point P on angle bisector of -BAC, at a distance r(√2) from A, if it has fallen on AB normally at a point Q such that QP =r. If the magnetic field is present, how much time the charged particle will take to come out of the magnetic field

mπBq
2mπBq
4mπBq
mπ2Bq
The correct Answer is:D
Since, QP=r,AP=r√2and∠AQP=90∘
AQ=rand∠QAP=45∘
The same logic concludes AR=r and ∠PAR=45∘
so, ∠QAR=90∘
r=mvBq
Distance travelled =πr2 ltbRgt Time=π2⋅mvBq⋅1v=mπ2Bq.

Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- Moving charges and magnetismBOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank
20 Videos
Similar Questions
The figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
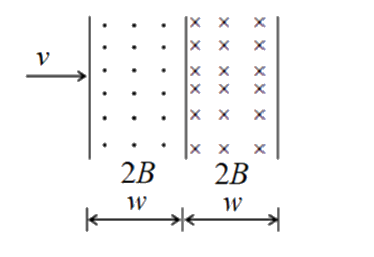
View SolutionThe radius of circular path for a charged particle of mass 'm' having charge q and kinetic energy K in a uniform , normal magnetic field B is ………………… .
View Solution
Knowledge Check
A charge q is moving in a magnetic field then the magnetic force does not depend upon
AChargeBMassCVelocityDMagnetic fieldA charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
Aincreases the K.E. of the particleBdecreases the K.E. of the particleCchanges the direction of motion of the particleDdoes both (a) and ( c)A charged particle enters a magnetic field at an angle of 90∘with the magnetic field. The path of the particle will be a/an
AHelixBEllipseCCircleDStraight line
the magnetic field shown in the figure consist of the two magnetic fields.
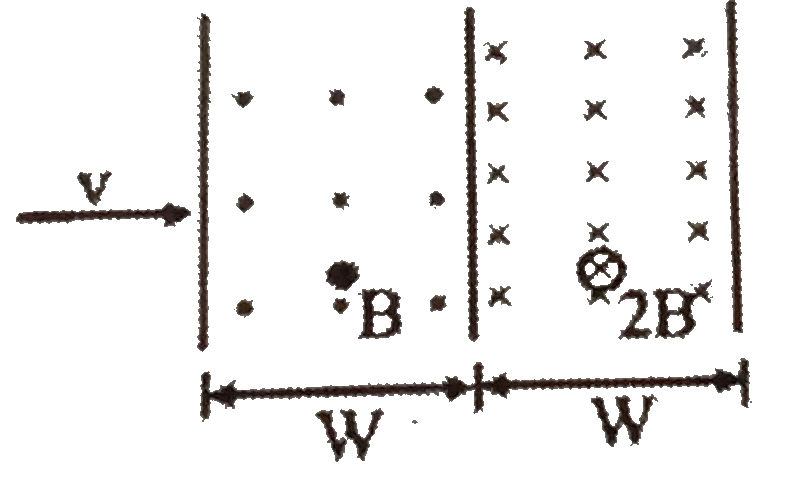
If v is the velocity just required for a charge particles of mass m and charge q to pass through the magnetic field. Particle is projected with velocity 'v' then how much time does such a charge spend in the magntic filed-
View SolutionA charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
View SolutionA charged particle is moving along a magnetic field line. The magnetic force on the particle is
View SolutionA charged particle is moved along a magnetic field line. The magnetic force on the particle is
View SolutionA charged particle of mass m is moving with a speed u in a circle of radius r. If the magnetic field induction at the centre is B, the charge on the particle is
View Solution
