The atomic mass $._{2}^{4} H e$ is $4.0026 u$ and the atomic mass of $._{1}^{1} H$ is $1.0078 u$ . Using atomic mass units instead of kilograms, obtain the binding energy of $._{2}^{4} H e$ nucleus.

Video Solution

Text Solution

Verified by Experts

To determine the binding energy, we calcualte the mass defect in atomic mass units and then use the fact that one atomic mass unit is equivalent to $931.5 M e V$ of energy. The mass of $4.0026 u$ for $._{2}^{4} H e$ inclides the mass defect, we must subtract $4.0026 u$ from the sum of the individual masses of the nucleons, including the mass to the electrons . As Fig. illustrates, the electron mass will be included if the masses of two hydrogen atoms are used in the calculation instead of the masses of two protons. The mass of a hydrogen atom is given as $1.0078 u$ , and the mass of a neutron is given in Table $5.1$ as $1.0087 u$ .
$._{2}^{4} H$

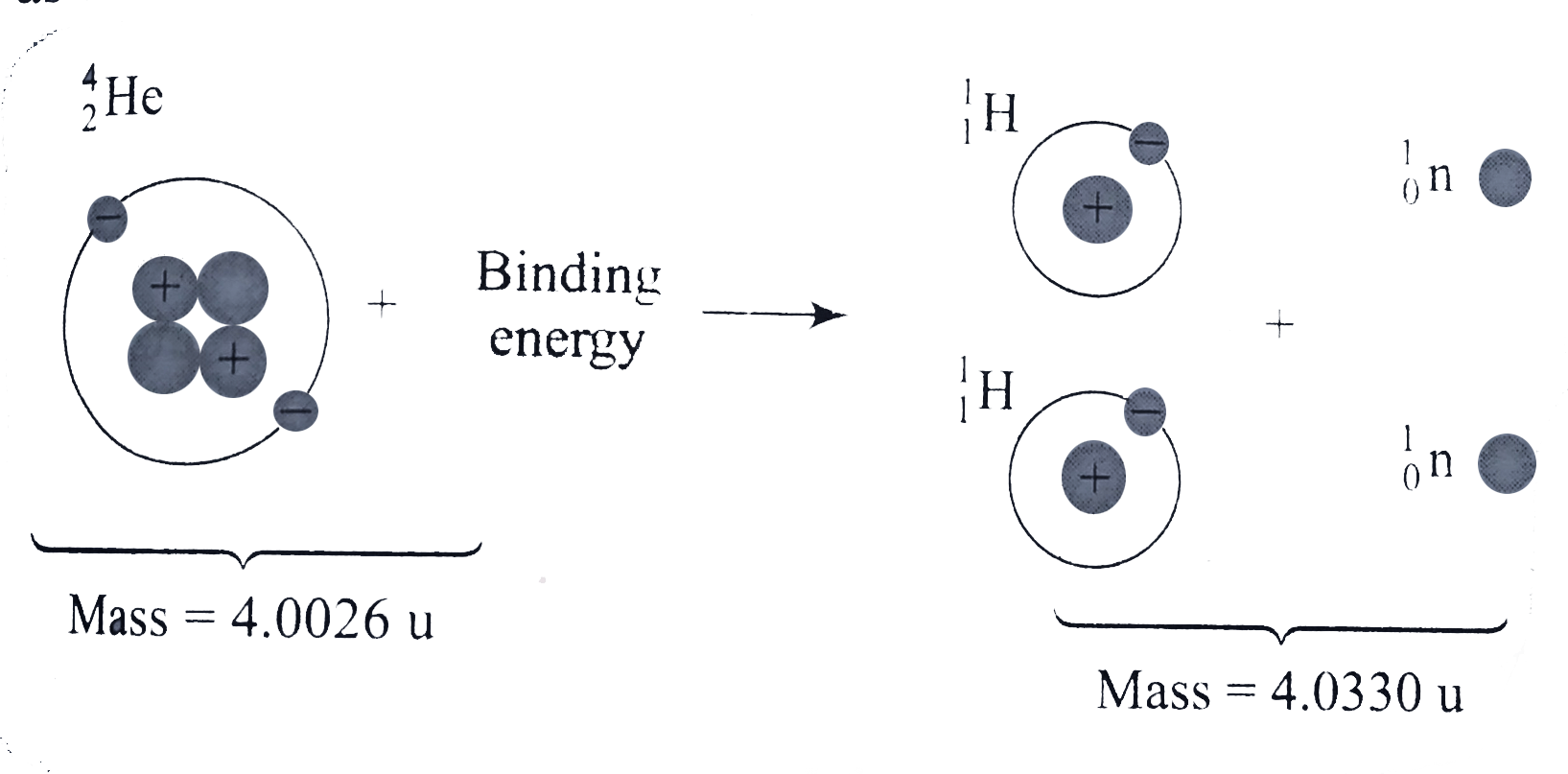
The sum of the individual masses is
$2 (1.0078 u)      \begin{matrix} Two hydrogen atoms \end{matrix} + \frac{2 (1.0087 u)}{Two neutrons} = 4.0330 u$
The mass defect is $Δ m = 4.0330 u - 4.0026 u = 0.0304 u$
Since $1 u$ is equivalent to $931.5 M e V$ , the binding energy is $28.3 M e V$ .

Updated on:21/07/2023

One atomic mass unit in kilogram is:
A $\frac{1}{N_{A}}$
B $\frac{12}{N_{A}}$
C $\frac{1}{1000 N_{A}}$
D $\frac{1000}{N_{A}}$
One atomic mass unit in kilogram is
A $1 / N_{A}$
B $12 / N_{A}$
C $1 / 1000 N_{A}$
D $1000 / N_{A}$
The mass of proton is $1.0073 u$ and that of neutron is $1.0087 u$ ( $u =$ atomic mass unit). The binding energy of $._{2} H e^{4}$ is (mass of helium nucleus $= 4.0015 u$ )
A $28.4$ MeV
B $0.061 u$
C $0.0305 J$
D $0.0305$ erg