In a set of experiment on a hydrogen on a hypothetical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state $(n = 1)$ are shown in the energy level diagram

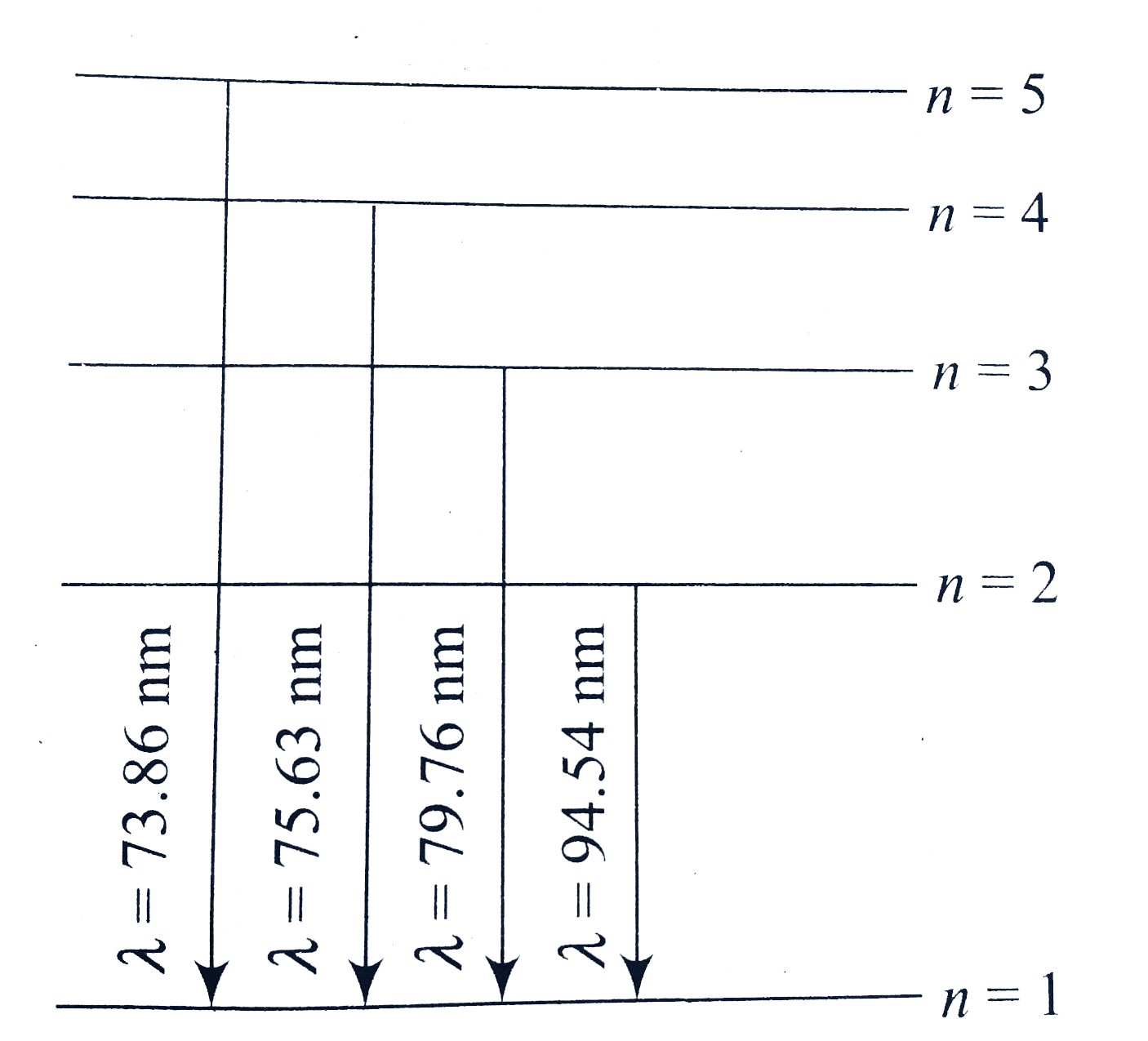
$λ_{5 \to 1} = 73.86 n m$
$λ_{4 \to 1} = 75.63 n m$
$λ_{3 \to 1} = 79.76 n m$
$λ_{2 \to 1} = 94.54 n m$
The energy of the atom in level $n = 1$ is nearly

A

$13.14 e V$

B

$15.57 e V$

C

$17.52 e V$

D

$16.42 e V$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$E_{1} = - 17.52 e V = Z^{2} E_{01} E_{2} - E_{1} = (\frac{E_{1}}{2^{2}} - E_{1})$
$\frac{h c}{λ_{2 \to 1}} = \frac{1242 e V n m}{94.54 n m} = 13.14 e V$
$E_{3} - E_{1} = \frac{h c}{λ_{3 \to 1}} = \frac{1242 e V n m}{79.76 n m} = 15.57 e V$
$E_{3} = - 1.95 e V$
$E_{4} - E_{1} = \frac{h c}{λ_{4 \to 1}} = \frac{1242 e V n m}{75.63 n m} = 16.42 e V$

|

Updated on:21/07/2023

Class 12 PHYSICS ATOMS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a set of experiment on a hydrogen on a hypothetical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state $(n = 1)$ are shown in the energy level diagram

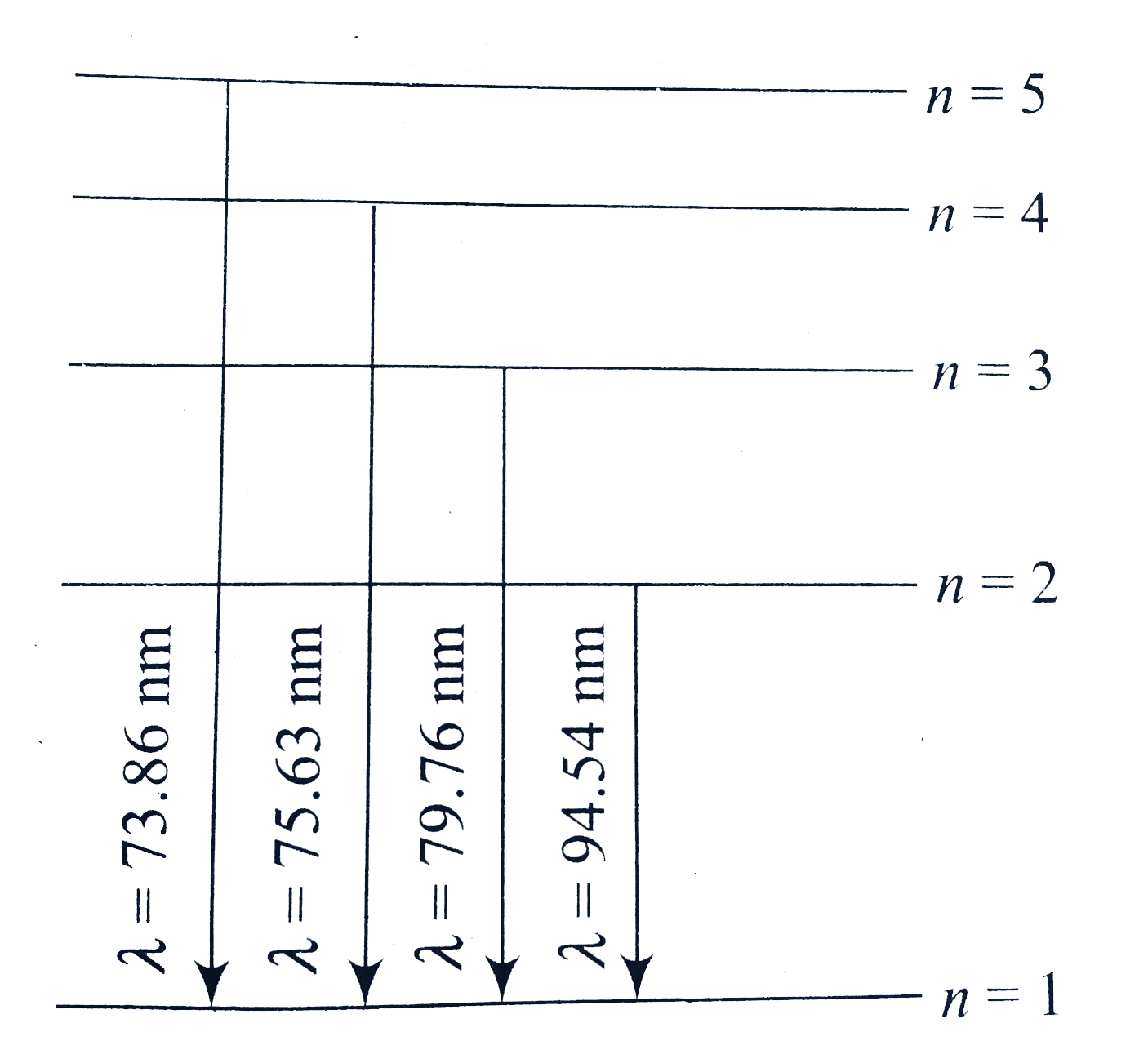
$λ_{5 \to 1} = 73.86 n m$
$λ_{4 \to 1} = 75.63 n m$
$λ_{3 \to 1} = 79.76 n m$
$λ_{2 \to 1} = 94.54 n m$
The possible energy of the atom in $n = 3$ cannot be
A $- 19.5 e V$
B $- 0.4875 e V$
C $- 0.121 e V$
D $- 7.8 e V$
Question 2 - Select One
In a set of experiment on a hydrogen on a hypothetical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state $(n = 1)$ are shown in the energy level diagram

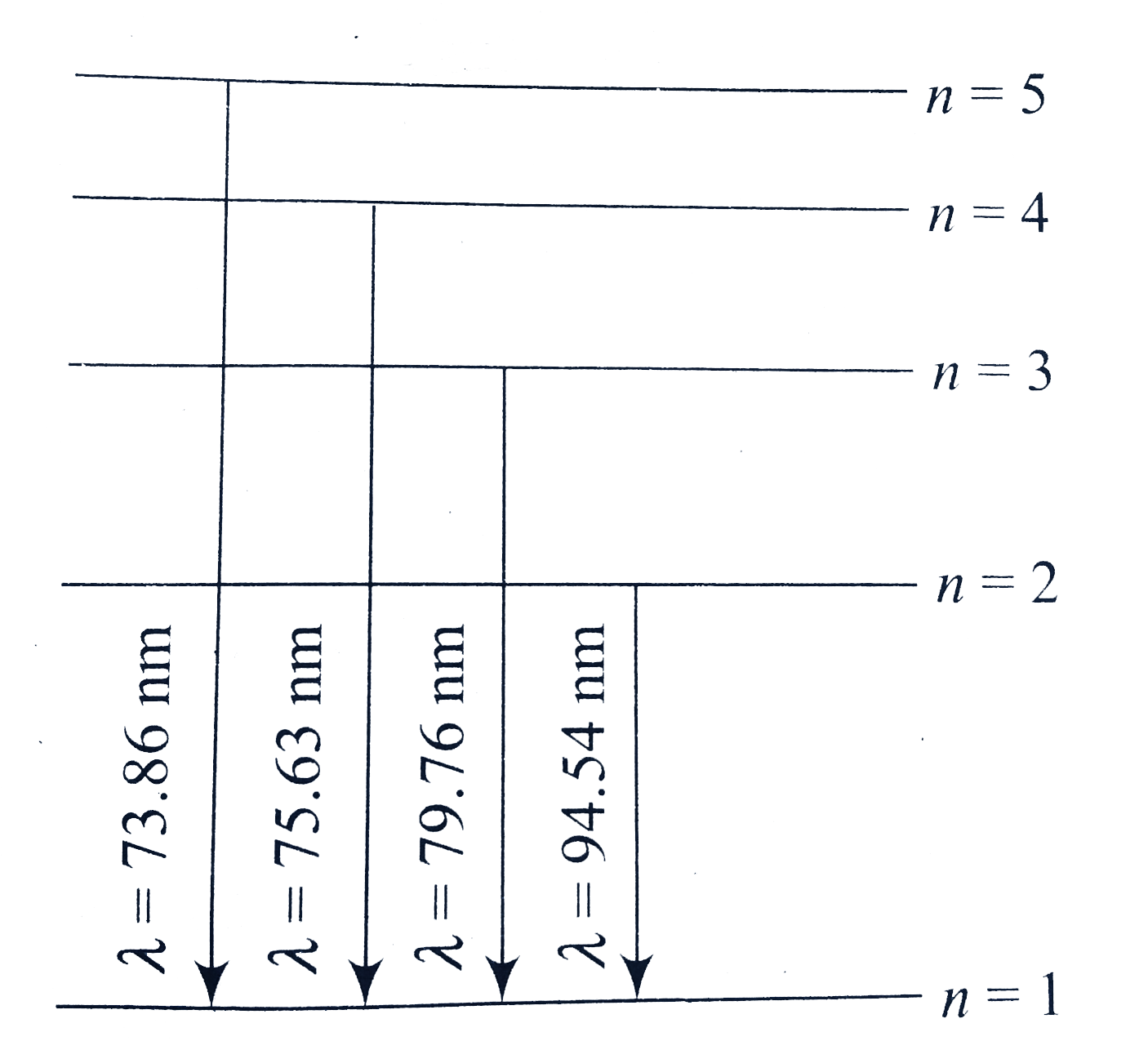
$λ_{5 \to 1} = 73.86 n m$
$λ_{4 \to 1} = 75.63 n m$
$λ_{3 \to 1} = 79.76 n m$
$λ_{2 \to 1} = 94.54 n m$
If an electron made a transition from n = 4 to n = 2 level, the wavelength of the light that it would emit is nearly
A $380 n m$
B $190 n m$
C $76 n m$
D $510 n m$
Question 3 - Select One
The wavelengths of photons emitted by electron transition between two similar leveis in H and $H e^{+}$ are $λ_{1}$ and $λ_{2}$ respectively. Then :-
A $λ_{2} = λ_{1}$
B $λ_{2} = 2 λ_{1}$
C $λ_{2} = λ_{1} / 2$
D $λ_{2} = λ_{1} / 4$

CENGAGE PHYSICS-ATOMIC PHYSICS-Linked Comprehension

Home
Ask Doubt
Profile