Let A0 be the area enclined by the orbit in a hydrogen atom .The graph of in (A0/A1) against ln(n)
will pass through origin
will be a straight line with slop 4
will be a monotonically increasing nonlinear curve
will be a circle
The correct Answer is:A, B
rn=n2r1
In (AnA1)=In((pin_(n^(2)))/(pir_(1)^(2)))<br>In n^(4) = 41n (n)
Topper's Solved these Questions
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Multiple Correct
Explore 13 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Linked Comprehension
Explore 62 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Subject
Explore 17 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICSChapter:ALTERNATING CURRENTExercise:QUESTION BANK
Explore 65 Videos
- ATOMSBook:CENGAGE PHYSICSChapter:ATOMSExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
The figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
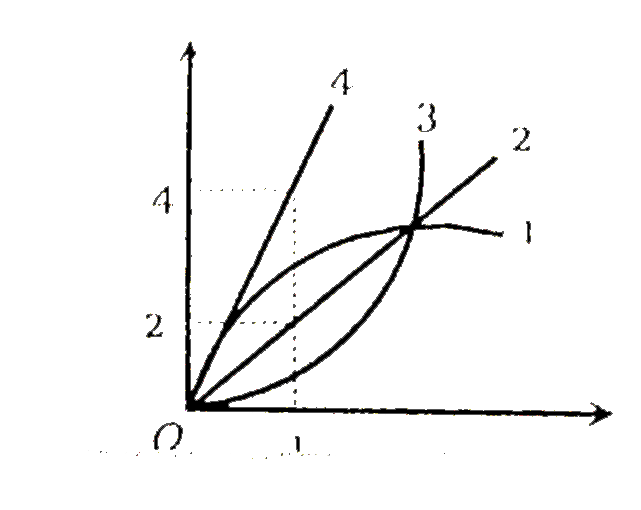
View SolutionFor a H-like species if area A1 is of ground state orbit and area An is of nth orbit, then, the plot of AnA1 us n2 looks like:
View Solution
Knowledge Check
Let A_(0) be the area enclined by the orbit in a hydrogen atom .The graph of in (A0/A1) againest in(pi)
Awill pass through the originBwill be a straigth line with slope 4Cwill be a monotonically increasing nonlinear curveDwill be a circleLet An be the area enclosed by the nth orbit in a hydrogen atom. The graph of ln(An/At) against In (n)
Awill pass through the originBwill have certain point lying on a straight line with slope 4Cwill be a monotonically increasing nonlinear curveDwill be a circleIn hydrogen atom, the area enclosed by nth orbit is An. The graph between log (AnA1) log will be
A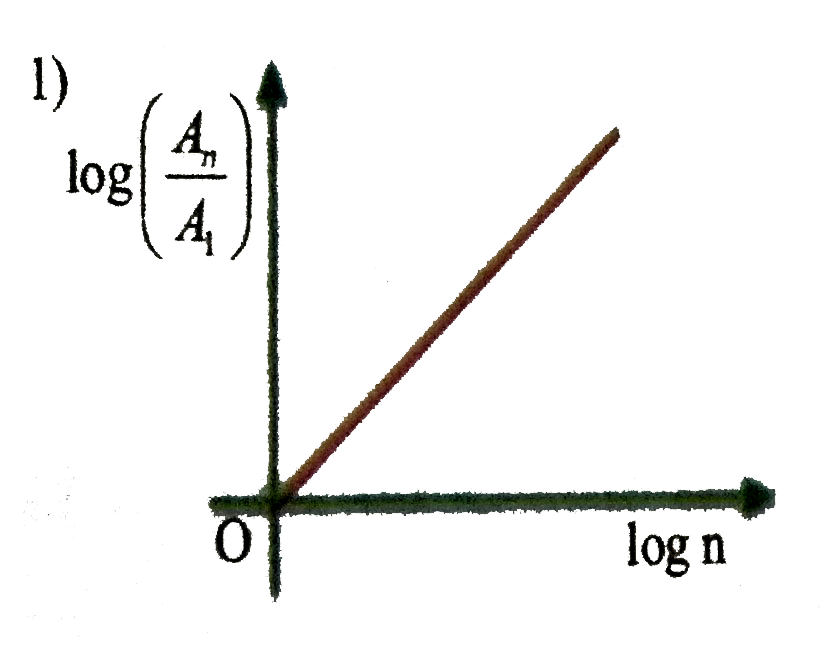 B
B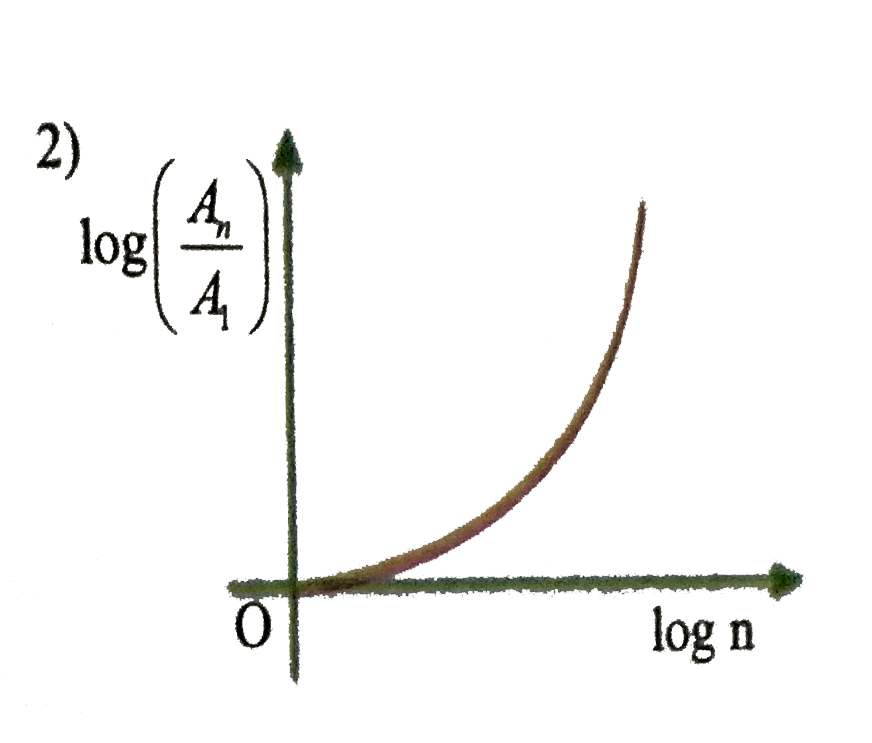 C
C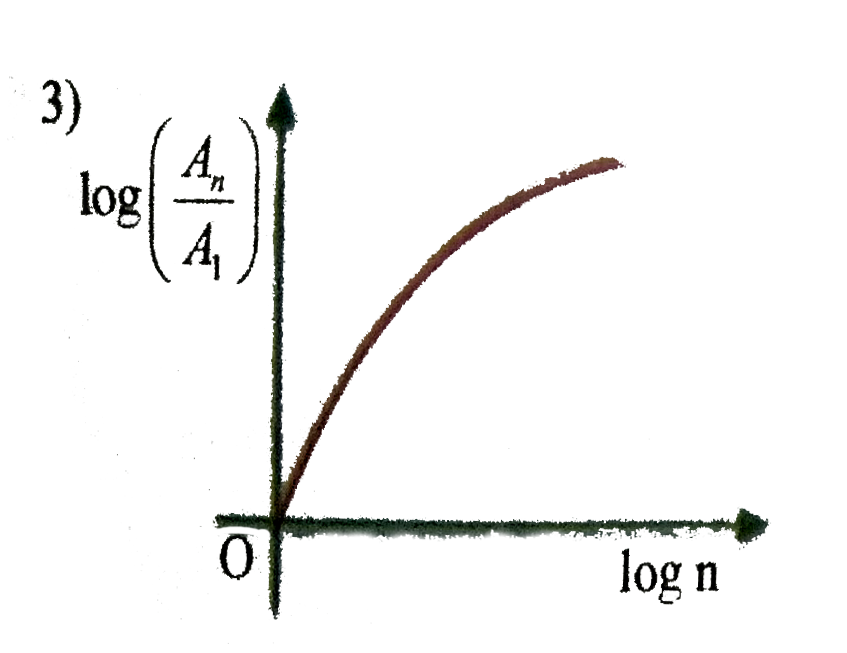 D
D
The magnitude of acceleration of the electron in the nth orbit of hydrogen atom is aH and that of singly ionized helium atom is aHe. The ratio aH:aHe is
View SolutionLet a0=0 and an=3an−1+1 for n≥1. Then the remainder obtained dividing a2010 by 11 is -
View SolutionLet a1,a2,a3 …. an be in G.P. If the area bounded by the curve y2=4anX and y2=4an(an−x) be An, then the sequence A1,A2,A3…….An are in
View SolutionLet A0A1A2A3A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A0A1,A0A2andA0A4 is
View SolutionLet a0=0 and an=3an−1+1 for n≥1. Then the remainder obtained dividing a2010 by 11 is
View Solution

