Energy E of a hydrogen atom with principle quantum number n is given by E=−13.6n2eV. The energy of a photon ejected when the electron jumps from n=3 state to n=2 state of hydrogen is approximately
1.9eV
2.3eV
3.4eV
4.5eV
The correct Answer is:A
13.6(122−132)eV=1.9eV
Topper's Solved these Questions
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Multiple Correct
Explore 13 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Linked Comprehension
Explore 62 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Subject
Explore 17 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICSChapter:ALTERNATING CURRENTExercise:QUESTION BANK
Explore 65 Videos
- ATOMSBook:CENGAGE PHYSICSChapter:ATOMSExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
Knowledge Check
The ionisation energy of hydrogen is 13.6 eV . The energy of the photon released when an electron jumps from the first excited state (n=2) to the ground state of hydrogen atom is
A3.4 eVB4.53 eVC10.2 eVD13.6eV
Read the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
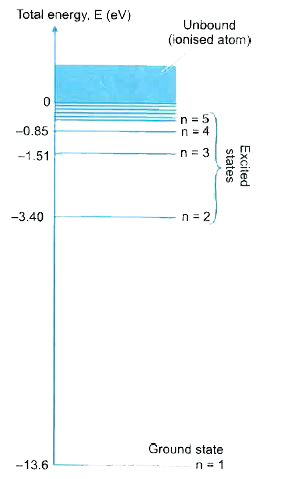
Now answer the follwoing questions:
When does a hydrogen atom emit a photon ?
View SolutionRead the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
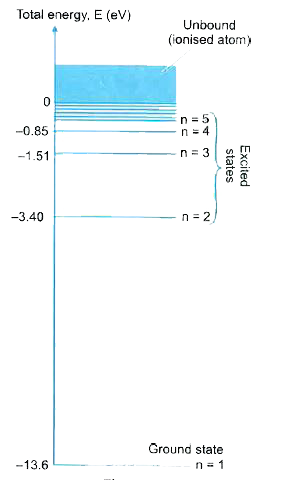
Now answer the follwoing questions:
How can a hydrogen atom receive energy to raise the electron to higher energy states ?
View SolutionRead the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
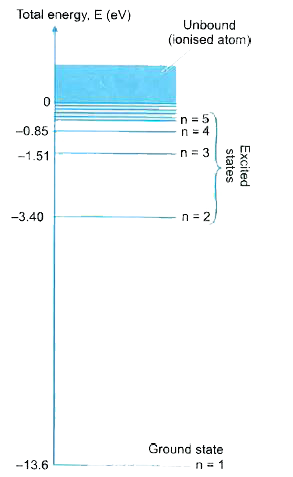
Now answer the follwoing questions:
Define ionisation energy of hydrogen atom and give its value.
View SolutionRead the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
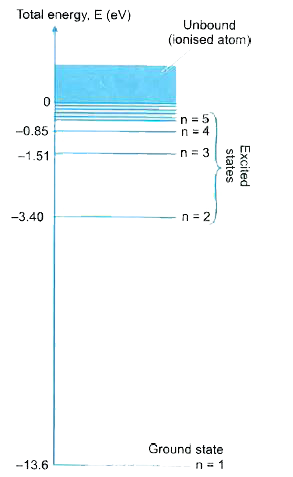
Now answer the follwoing questions:
What is the energy of hydrogen atom and give its value.
View SolutionRead the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
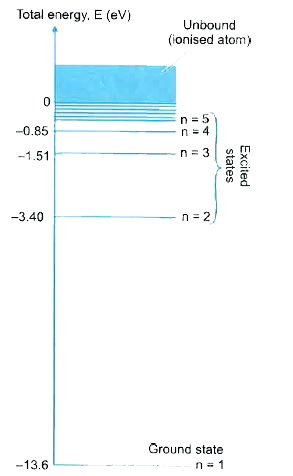
Now answer the follwoing questions:
Name the spectral series of hydrogen atom observed in visible light region.
View SolutionRead the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
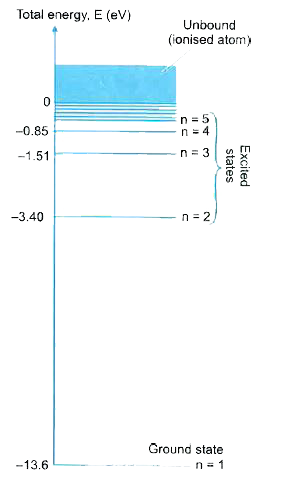
Now answer the follwoing questions:
Which atomic transition correspond to spectral lines of hydrogen in visible light ?
View SolutionRead the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
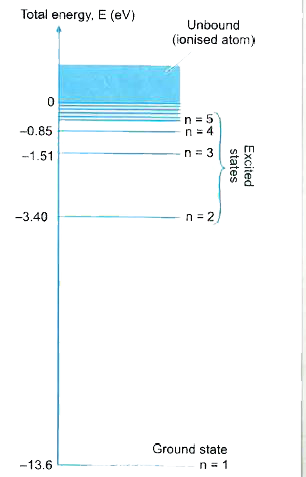
Now answer the follwoing questions:
Write the formula for spectral lines the of hydrogen atom in visible light in terms of Rydberg's constant.
View Solution

