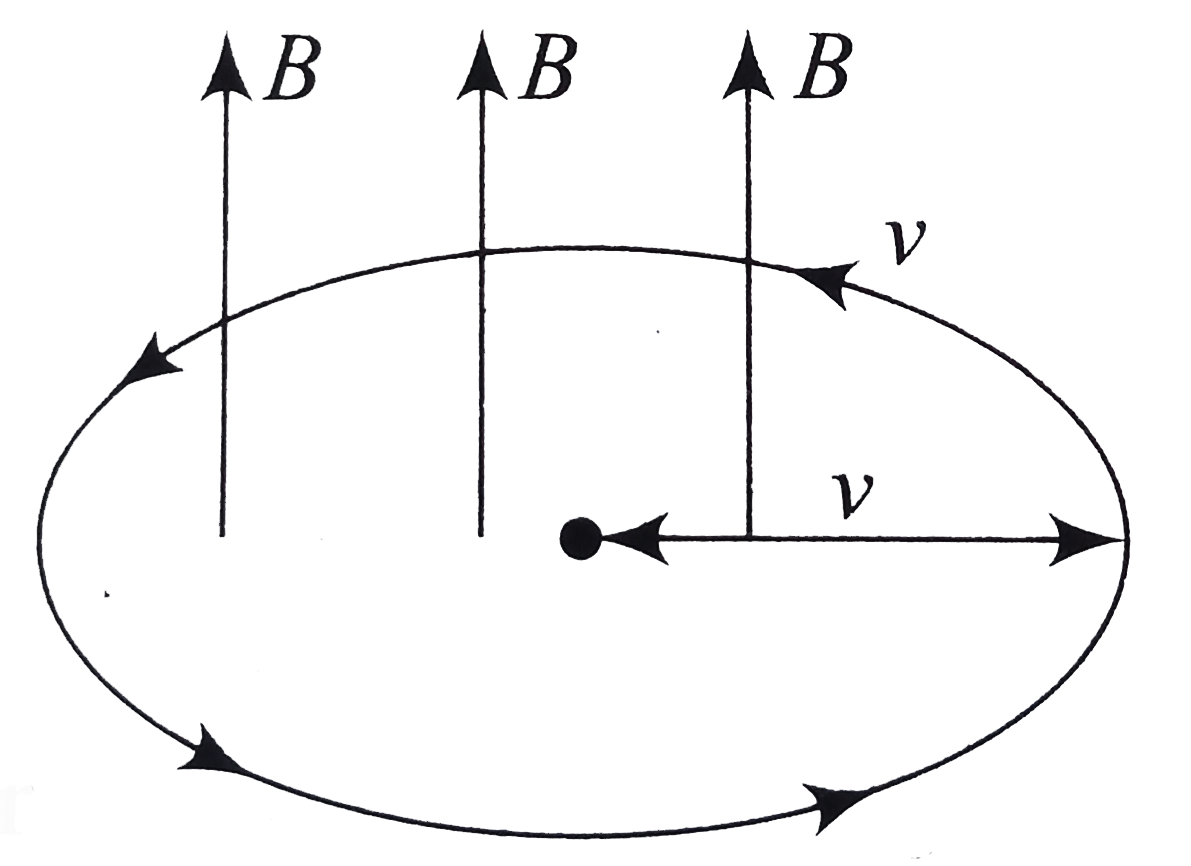
An electron is orbiting is a circular orbit of radius r under the influence of a constant magnetic field of strength B. Assuming that Bohr postulate regarding the quantization of angular momentum holds good for this electron, find
(a) the allowed values of te radius r of the orbit.
(b) the kinetic energy of the electron in orbit
(c ) the potential energy of interaction between the magnetic moment of the orbital current due to the electron moving in its orbit and the magnetic field B.
(d) the total energy of the allowed energy levels.
(e) the total magnetic flux due to the magnetic field B passing through the nth orbit. (Assume that the charge on the electron is -e and the mass of the electron is m).
Video Solution
Text Solution
The correct Answer is:a √na0, (b). 12nh(eBm), ( c).12nh(eBm) d.nh(eBm), e.(nh2e)
mv2r=eVB
or vr=vR=cBm(i)
Using Bohr quantization condition.
mvr=nh2π=nh,→integer
or vr=nhm (ii)
a. r2=nhBe
or r=√n√hBe=√na0 (iii)
b. T(kinetic energy)=12mv2
=m2v22m=12m×n2h2r2
=12m×2hBe=12nh(Bem) (iv)
c.
The time period of revolution of the electron.
τ=2πrv=2πmBe
The corrent, i=eτ=e2B2πm=e2mnh
The potential energy of interaction
U=−¯¯μ¯¯¯B=12nh(eBm) (v)
d. The total energy .
E=T+U=nh(eBm) which is quantized.
e. The total magnetic flux through the nth orbit.
ϕ=πr2B=π(nhBe) (vi)
|
Topper's Solved these Questions
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Single Correct
Explore 187 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Multiple Correct
Explore 13 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Exercise 4.2
Explore 12 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICSChapter:ALTERNATING CURRENTExercise:QUESTION BANK
Explore 65 Videos
- ATOMSBook:CENGAGE PHYSICSChapter:ATOMSExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
Knowledge Check
An electron moving in a circular orbit of radius R with frequency f. The magnetic field at the centre of the orbit is
Aμ0ef2πRBμ0ef2RCμef22RDzeroThe kinetic energy of the electron in an orbit of radius r in hydrogen atom is (e= electronic charge)
Ae2r2Be22rCe2rDe22r2An electron revolve round the nucleous with the radius of the circular orbit is 'r' . To double the kinetic energy of the electron its orbital radius will be
Av/√2B√2rC2rDr/2
The orbital angular momentum of an electron in 2s-orbital is
View SolutionAn electron revolves in a circular orbit of radius r with angular speed ω . The magnetic field at the centre of electron orbit is
View SolutionIf the radius of the Bohr's orbit is r then the de Broglie wavelength of the electron in the third orbit will be
View SolutionAn clectron moving in a circular orbit of radius r makes rotations per second. The magnetic moment of the orbital electron is
View SolutionThe ratio of kinetic energy of an electron in Bohr's orbit to its total energy in the same orbit is ______
View Solution
