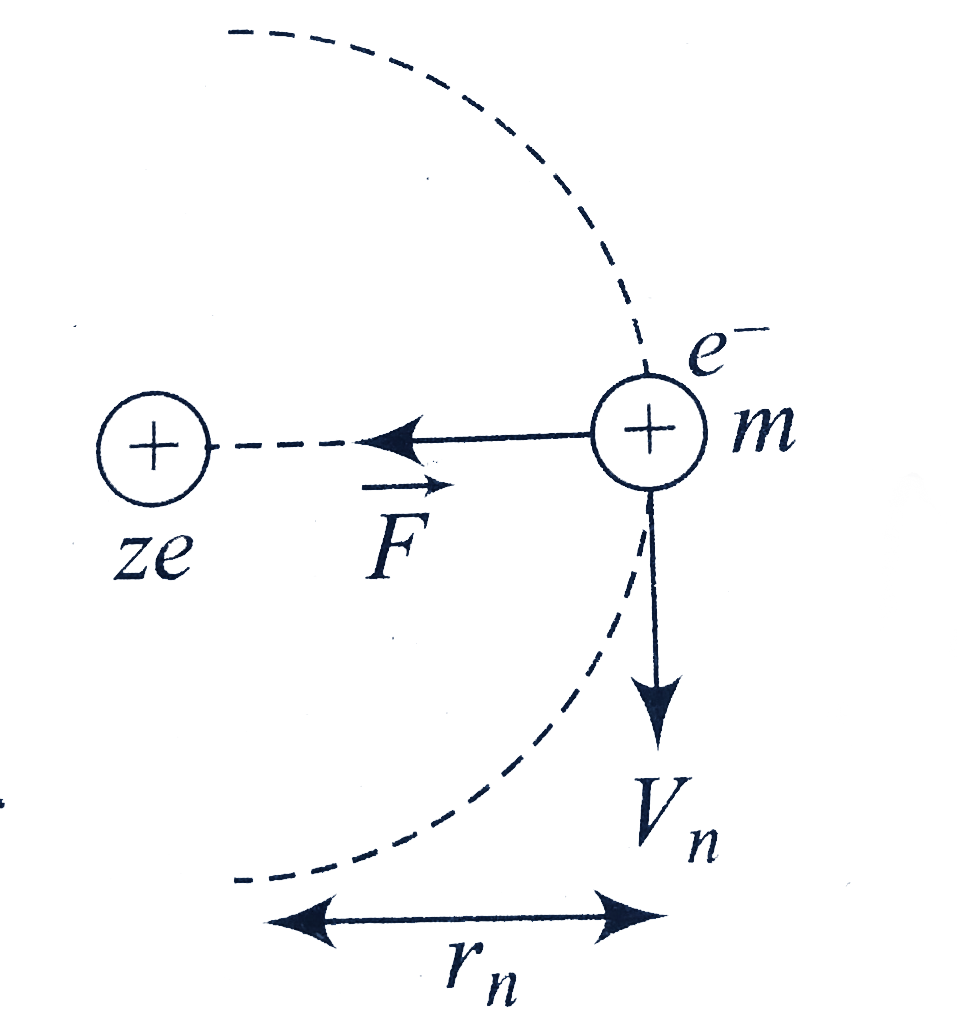
According to classical physics, an electron in periodic motion with emit electromagnetic radiation with the same frequency as that of its revolution. Compute this value for hydrogen atom in nth quantum theory permit emission of such photons due to transition between adjoining orbits ? Discuss the result obtained.
The orbital frequency of nth orbit is given by
vn=(electron speed)/(orbital circumference)
=e22nhε0×12π×πme2n2ε0h2=me44ε20n3h3
[AsK=14πε0
From the lows of electromagnetic theory, the frequency of the radition emitted by this electron will also be vn
According to Bohr's theory , the frequency of the radition for the adjoining orbits is given by
v0=En−En−1h=me48ε20h2[1(n−1)2−1n2]
me48ε20h2(2n−1)(n−1)2×n2
A comprison of this expression with the classic expression above show that the difference in their prediction will be large for small n, i.e. , for n=2,1/n3=1/8 and (2n−1)/2n2(n−1)2=3/8, so that the frequency given by quantum theory is 3 times that calculate from classic theory. However , for very large n , the quantum expression reduced to that obtained from classical theory because for n→∞
⎛⎜⎝2n−12n2(n−1)2×2n2n2n2⎞⎟⎠=1n3
Consequentiy , the predictions of Bohr's theory agrees with that of the classical theory in the limit of very large quantum numbers . This correspondence is called as bohr's correspondenceprincipal.
Topper's Solved these Questions
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Exercise 4.2
Explore 12 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Subject
Explore 17 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICSChapter:ATOMIC PHYSICSExercise:Solved Examples
Explore 23 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICSChapter:ALTERNATING CURRENTExercise:QUESTION BANK
Explore 65 Videos
- ATOMSBook:CENGAGE PHYSICSChapter:ATOMSExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
According to classical electromagnetic theory, calculate the initial frequency of the light emitted by the electron revolving around a proton in hydrogen atom.
View SolutionAccording to Maxwell's theory of electron dynamics, an electron going in a circle should emit radiation of frequency equal to its frequency of revolution. What should be the wavelength of the radiation emitted by a hydrogen atom in the ground state if this rule is followed?
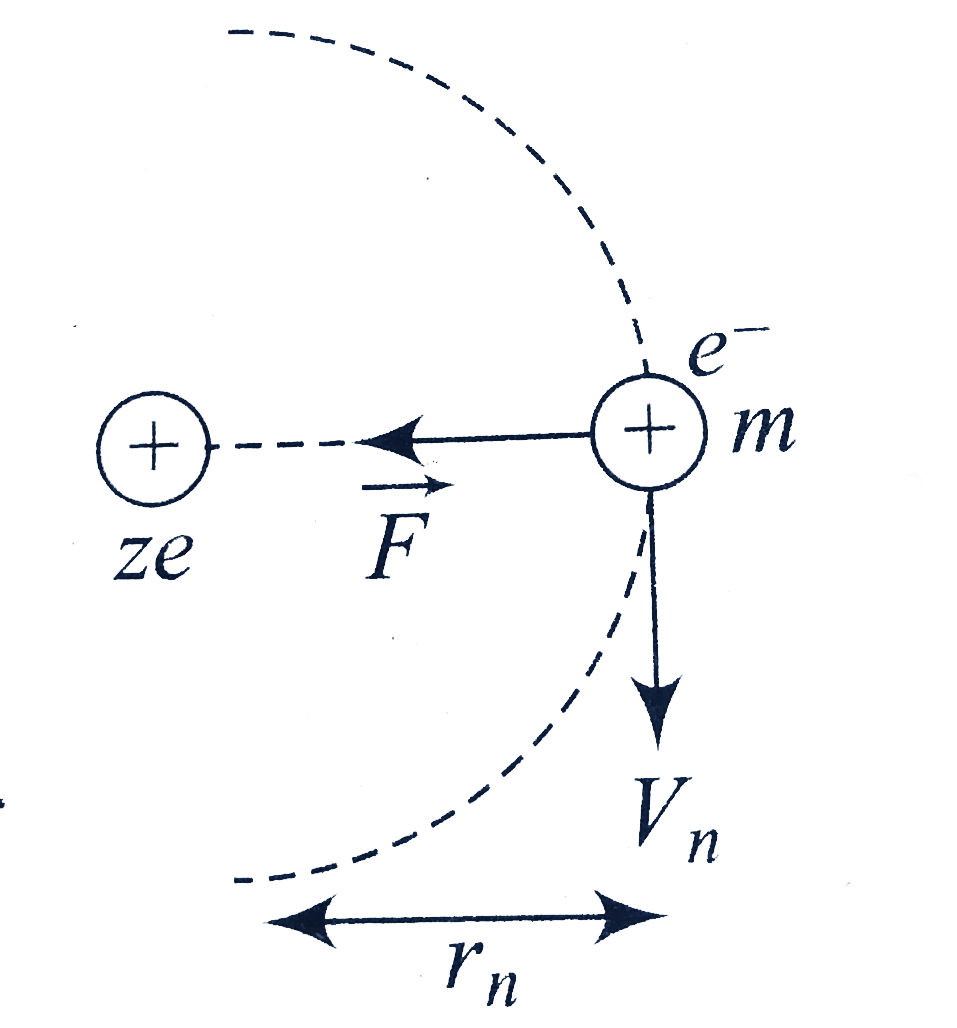
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the velocity of electron is v0 when the hydrogen atom is in the ground state on the other planet should be
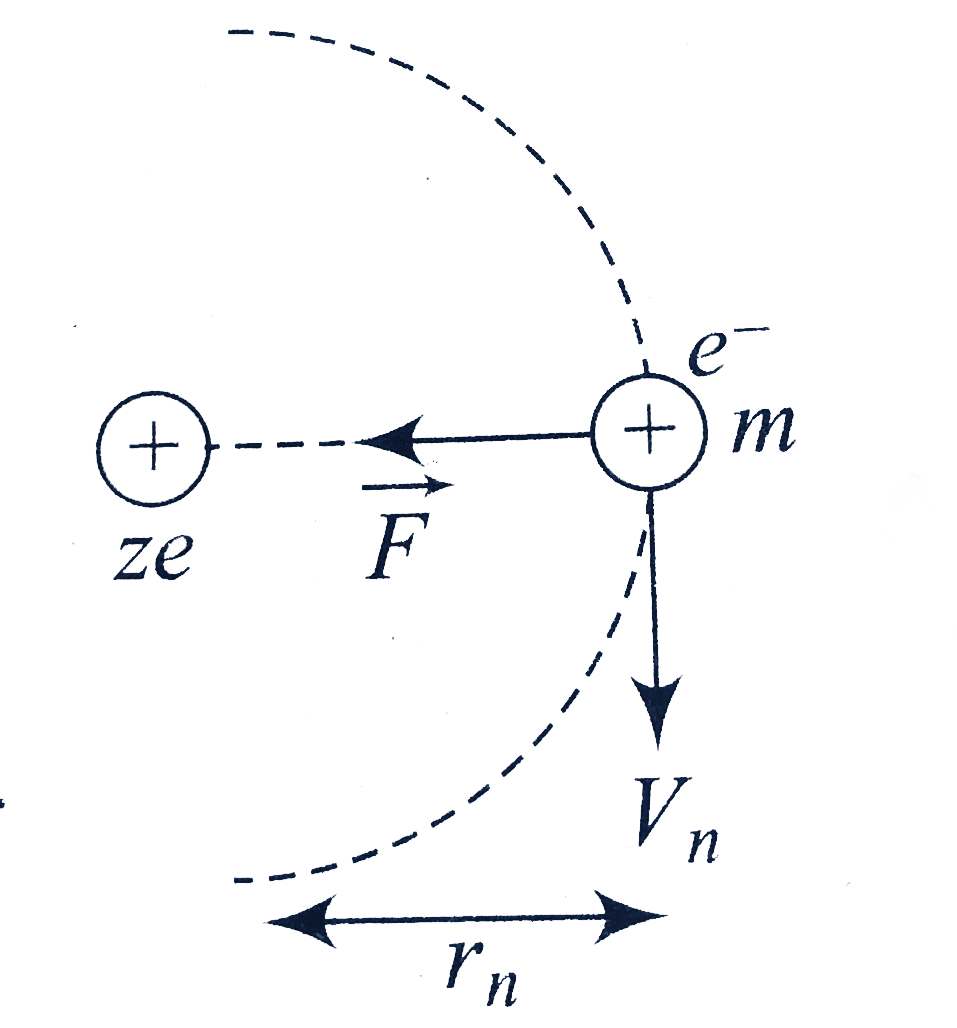
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the ionization potential energy of a hydrogen atom is 13.6eV. On the other planet, this ionization potential energy will be
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
The minimum permissible radius of the orbit will be
View SolutionUsing Bohr's theory show that when n is very large the frequency of radiation emitted by hydrogen atom due to transition of electrom from n to (n−1) is equal to frequency of revolution of electron in its orbit.
View SolutionIf the wavelength of photon emitted due to transition of electron from third orbit to first orbit in a hydrogen atom is λ then the wavelength of photon emitted due to transition of electron from fourth orbit to second orbit will be
View SolutionShow that for large values of principal quantum number, the frequency of an electron rotating in adjacent energy levels of hydrogen atom and the radiated frequency for a transition between these levels all approach the same value.
View SolutionCalculate the ratio of the frequencies of the radiation emitted due to transition of the electron in a hydrogen atom from its (i) second permitted energy level to the first level and (ii) highest permitted energy level to the second permitted level .
View SolutionCalculate the ratio of the frequencies of the radiation emitted due to transition of the electron in a hydrogen atom from its (i) second permitted energy level to the first level, and (ii) highest permitted energy level to the second permitted level.
View Solution

