In the path of a uniform light beam of large cross-sectional area and intensity I. a solid sphere of redius R which is perfectly reflecting is placed . Find the force exerted on this sphere due to the light beam.

Video Solution

Text Solution

Verified by Experts

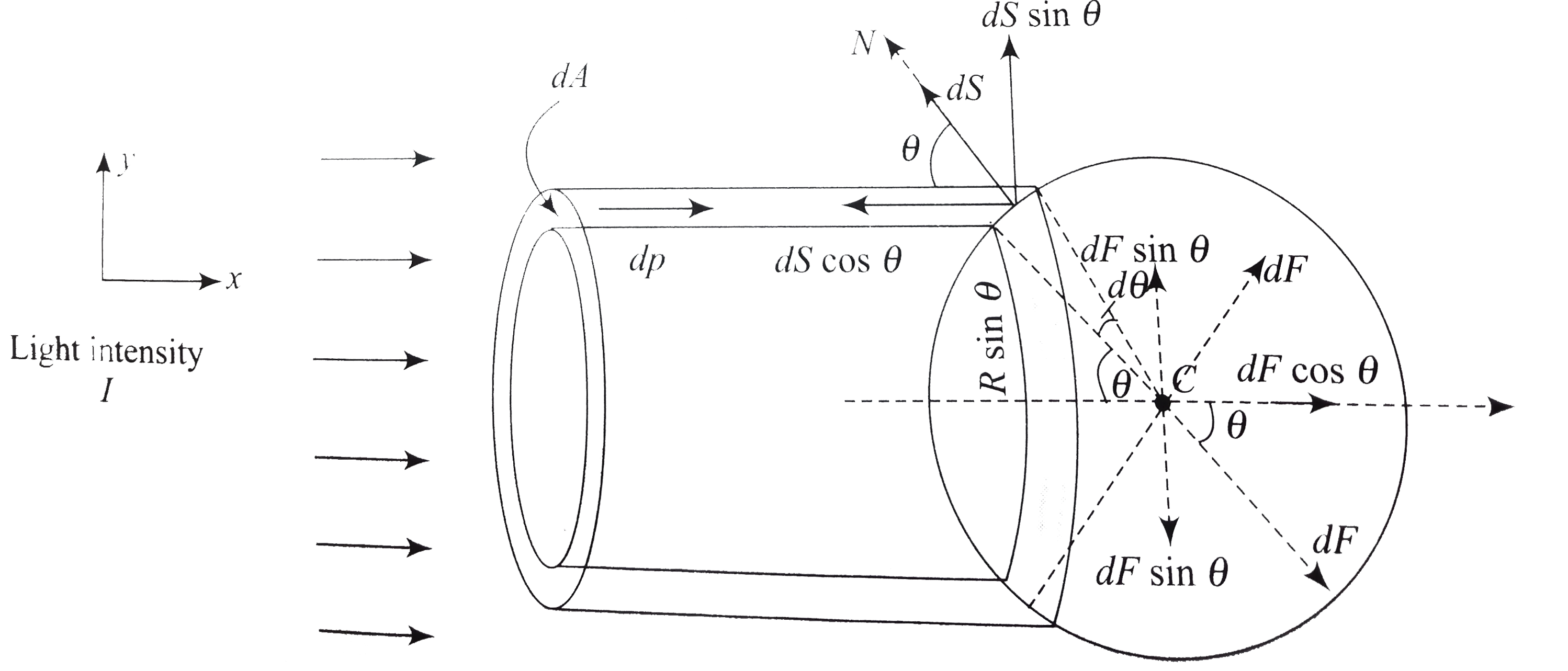
The front surface of the sphere will be illuminated by the light as shown in Fig as angle of incidence of light is different position of the front face of the sphere.
We can cosider a small elemental circular strip (ring) of angular width $d t h η$ on its surface at an angle $θ$ from its horizontal diameter as shown . Let the area of this elemental strip is dS, then
$d S = 2 θ R sin θ R d$ $θ$ ...(i)
$R sin θ$ is the radius of this circular strip (ring).
We take the projection of area of this slant elemental circular strip in vertical plane. Let dA be the projection of the slant strip area dS along the cross-sectional plane of the light beam and it is given as
$d A = d S cos θ$ ....(ii)
Hence, the power of light incident on this strip is $d P = I d A$ . The momentum of photons per second incident on this strip is $d A = \frac{d P}{c} = \frac{I d A}{c}$ ....(iii)
These photons are incident at an angle $θ$ to the normal N of this strip. As the surface of the sphere is perfectly reflecting, the photons will be reflected at the same angle $θ$ to N as shown in the figure.
Hence, the change in linear momentum of photons is along the normal and thus force exerted on this strip along the normal is
$d F = 2 d p cos θ = \frac{2 I d A}{c} cos θ$ ...(iv)
Thus, the net force on sphere will be along the x-axis only.
Thus, the force on the sphere will be given as
$F \int d F cos θ = \int \frac{2 I d A}{c} {cos}^{2} θ$
$= \int_{0}^{\frac{π}{2}} \frac{2 I}{c} (2 π R sin θ cos θ R d θ) {cos}^{2} θ$
$\frac{4 I π R^{2}}{c} \int_{0}^{\frac{π}{2}} {cos}^{3} θ sin θ d θ = \frac{4 I π R^{2}}{c} {[- \frac{{cos}^{4}}{4}]}_{0}^{\frac{π}{2}}$
$\frac{I π R^{2}}{c} [1 - 0] = \frac{I π R^{2}}{c}$ ...(v)

Updated on:21/07/2023

|

Class 12 PHYSICS DUAL NATURE OF RADIATION AND MATTER

Topper's Solved these Questions

Similar Questions

Knowledge Check

If a parallel beam of light having intensity I is incident normally on a perfectly reflecting surface, the force exerted on the surface, equal F. When the surface is held at an angle $θ$ , the force is
A $2 F tan θ$
B $F cos θ$
C $2 F {cos}^{2} θ$
D2F

CENGAGE PHYSICS-PHOTOELECTRIC EFFECT-Integer Type

Home
Ask Doubt
Profile