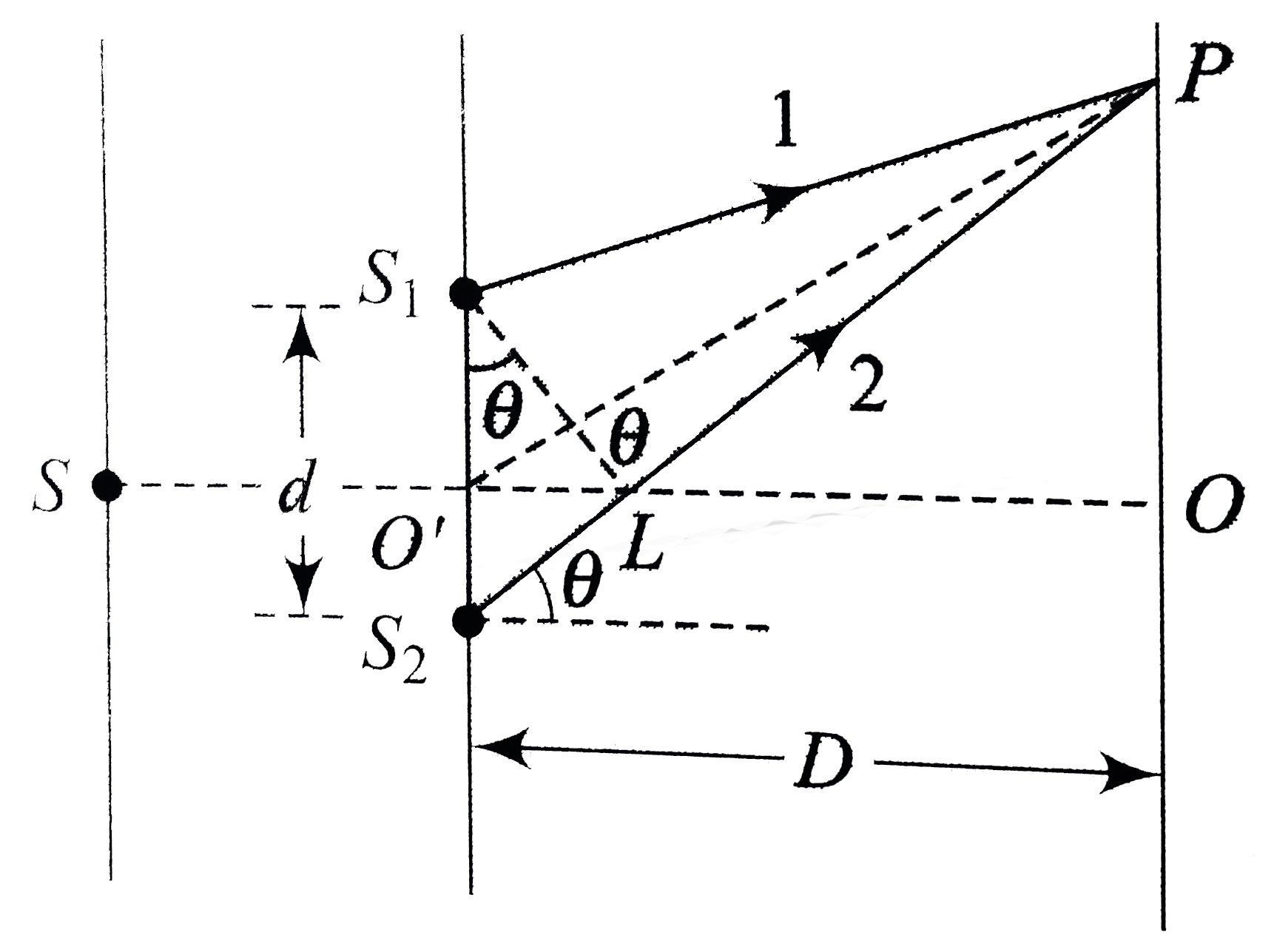
In Young's experiment, light of wavelength 600 nm falls on the double slits separated by 0.1 mm. What is the highest order of maximum intensity in the interference pattern obtained on a screen kept 3 m from the slits? How does the highest order change if the distance of screen from the slits is changed?

Video Solution

Text Solution

Verified by Experts

As we know, $n_{max} = \frac{d}{λ}$
Given $d = 0.1 m m = 0.1 \times 10^{- 3} m$
and $λ = 600 n m = 600 \times 10^{- 9} m .$
$∴ n_{max} = \frac{0.1 \times 10^{- 3}}{600 \times 10^{- 9}} = 166.67 \Rightarrow n_{max} = 166$
Obviously, $n_{max} = d / λ$ does not depend on the distance of screen form the slits.
Hence, it remains 166 if the distance between the slits and the screen is changed.

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The figure shows the interference pattern obtained in a double-slit experiment using light of wavelength 600 nm.

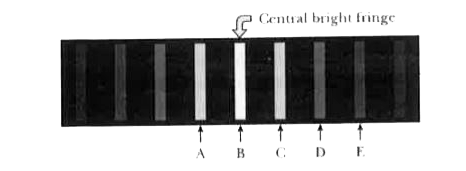
Which fringe is the same distance from both slits?
AA
BC
CB
DD
Question 2 - Select One
In Young's double slit experiment the two slits are d distance apart. Interference pattern is observed on a screen at a distance D from the slits. A dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light is
A $\frac{D^{2}}{2 d}$
B $\frac{d^{2}}{2 D}$
C $\frac{D^{2}}{d}$
D $\frac{d^{2}}{D}$
Question 3 - Select One
In Yonung's double-slit experiment, two slits which are separated by 1.2 mm are illuminated with a monochromatic light of wavelength $6000 Å$ The interference pattern is observed on a screen placed at a distance of 1 m from the slits. Find the number of bright fringes formed over 1 cm width on the screen.
A25
B12
C15
D20

CENGAGE PHYSICS-WAVE OPTICS-QUESTION BANK

Home
Ask Doubt
Profile