A concave lens of glass, refractive index 1.5, has both surfaces of same radius of curvature R. On immersion in a medium of refractive index 1.75, it will behave as a
convergent lens of focal length 3.5R
convergent lens of focal length 3.0R
divergent lens of focal length 3.5R
divergent lens of focal length 3.0R
The correct Answer is:A
According to lensmaker's formula,
1f=(.mgμ−1)(1R1−1R2)
Now, .mgμ=.gμ.mμ=1.51.75
For concave lens, as shown in figure, in this case R1=−R and R2=+R
∴1f=(1.51.75−1)(−1R−1R)=+0.25×21.75R
⇒f=+3.5R
The positive sign shows that the lens behaves as a convergent lens.
(a) is the correct option.

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Multiple Correct Answers Type8videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig Type2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - True/False5videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK1videos
FRICTION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank39videos
GRAVITATION
Similar Questions
A convax lens of glass ,refractive index1.5,has both surfaces of same radius of curvature R.On immersion in a medium of refractive index1.75,it wuill behaves as a
(A)convergent lens of focal length 3.5R(B)convergent lens of focal length 3.0R(C)divergent lens of focal length 3.5R(D)divergent lens of focal length 3.0RView SolutionA convex lens made up of glass of refractive index 1.5 is dippedin turn
(i) in a medium of refractive index 1.65
(ii) in a medium of refractive index 1.33
Then Will it behave as converging or diverging lens in the two cases ?View Solution
Knowledge Check
- Question 1 - Select One
A concave lens of glass, refractive index 1.5, has both surface of same radius of curvature R. On immersion in a medium of refractive index 1.75, it will have as a
Aconvergent lens of focal length 3.5R.Bconvergent lens of focal length 3.0R.Cdivergent lens of focal length 3.5R.Ddivergent lens of focal length 3.0R.
A convex lens made up of glass of refractive index 1.5 is dippedin turn
(i) in a medium of refractive index 1.65
(ii) in a medium of refractive index 1.33
(a) Will it behave as converging or diverging lens in the two cases ?
(b) How will its focal length changes in the two media ?View SolutionA convex lens made up of glass of refractive index 1.5 is dippedin turn
(i) in a medium of refractive index 1.65
(ii) in a medium of refractive index 1.33
(a) Will it behave as converging or diverging lens in the two cases ?
(b) How will its focal length changes in the two media ?View SolutionA convex lens made up of glass of refractive index 1.5 is dipped, in turn, in (i) a medium of refractive index 1.65, (ii) a medium of refractive index 1.33.
(a) Will it behave as a converging or a diverging lens in the two cases ?
(b) How will its focal length change in the two media ?View SolutionA diverging lens of refractive index 1.5 and focal length 15cm in air has same radii of curvature for both sides. If it is immersed in a liquid of refractive index 1.7, calculate focal length of the lens in liquid.
View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is
 View Solution
View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is
 View Solution
View SolutionThe figure below shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. Another thin lens of refractive index μ3 has same radius of curvature R on the two surface between the plano-convex and plano-concae lenses that the plane surfaces are parallel to each other. Find the focal length of the combination.
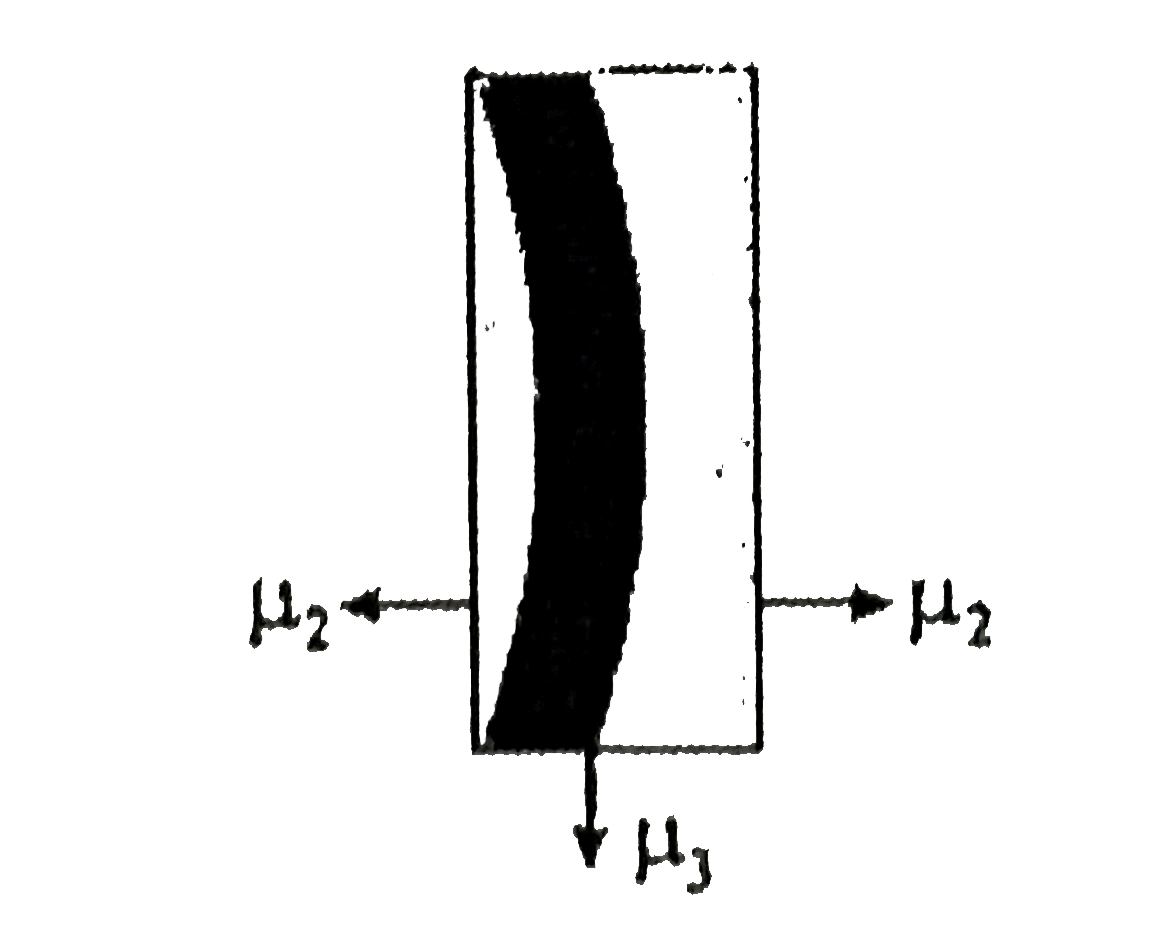 View Solution
View Solution

