A man is standing at distance x from a plane mirror in front of him. He wants to see the entire wall in mirror which is at distance. y behind the man. Find the minimum size of the mirror required.
To find the minimum size of the mirror required for a man standing at a distance x from a plane mirror to see an entire wall at a distance y behind him, we can follow these steps:
1. Understand the Setup:
- The man is standing at a distance x from the mirror.
- The wall is located at a distance y behind the man.
- We need to determine the minimum height of the mirror that allows the man to see the entire wall.
2. Define Variables:
- Let h be the height of the wall.
- Let d1 be the distance from the man's eyes to the top of the wall in the mirror.
- Let d2 be the distance from the man's eyes to the bottom of the wall in the mirror.
3. Use Geometry:
- The rays from the top of the wall to the mirror and then to the man's eyes will form a triangle.
- Similarly, the rays from the bottom of the wall to the mirror and then to the man's eyes will also form a triangle.
4. Apply Trigonometry:
- For the top of the wall:
tan(θ1)=d1x
- For the bottom of the wall:
tan(θ2)=d2x+y
5. Express Distances:
- From the above equations, we can express d1 and d2:
d1=xtan(θ1)
d2=(x+y)tan(θ2)
6. Total Height:
- The total height h of the wall can be expressed as the sum of the distances:
h=d1+d2
- Substituting the expressions for d1 and d2:
h=xtan(θ1)+(x+y)tan(θ2)
7. Combine Terms:
- Rearranging gives:
h=x(tan(θ1)+tan(θ2))+ytan(θ2)
8. Solve for Mirror Height:
- The minimum height of the mirror H required will be:
H=x(tan(θ1)+tan(θ2))
- From the previous equation, we can express tan(θ1)+tan(θ2) in terms of h:
tan(θ1)+tan(θ2)=h2x+y
- Therefore, substituting this back into the equation for H:
H=x⋅h2x+y
9. Final Result:
- The minimum size of the mirror required is:
H=xh2x+y
- The man is standing at a distance x from the mirror.
- The wall is located at a distance y behind the man.
- We need to determine the minimum height of the mirror that allows the man to see the entire wall.
- Let h be the height of the wall.
- Let d1 be the distance from the man's eyes to the top of the wall in the mirror.
- Let d2 be the distance from the man's eyes to the bottom of the wall in the mirror.
- The rays from the top of the wall to the mirror and then to the man's eyes will form a triangle.
- Similarly, the rays from the bottom of the wall to the mirror and then to the man's eyes will also form a triangle.
- For the top of the wall:
tan(θ1)=d1x
- For the bottom of the wall:
tan(θ2)=d2x+y
- From the above equations, we can express d1 and d2:
d1=xtan(θ1)
d2=(x+y)tan(θ2)
- The total height h of the wall can be expressed as the sum of the distances:
h=d1+d2
- Substituting the expressions for d1 and d2:
h=xtan(θ1)+(x+y)tan(θ2)
- Rearranging gives:
h=x(tan(θ1)+tan(θ2))+ytan(θ2)
- The minimum height of the mirror H required will be:
H=x(tan(θ1)+tan(θ2))
- From the previous equation, we can express tan(θ1)+tan(θ2) in terms of h:
tan(θ1)+tan(θ2)=h2x+y
- Therefore, substituting this back into the equation for H:
H=x⋅h2x+y
- The minimum size of the mirror required is:
H=xh2x+y
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Exercise1.2
Explore 20 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Exercise1.3
Explore 25 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Solved Examples
Explore 15 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:QUESTION BANK
Explore 1 Video
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
Similar Questions
A man is standing in aroom of length 20m and height 3m at a distance 5m from one wall. On the facing wall a mirror is hanging. Find the minimum size of mirror required in which man will be able to see complete height of wall behind him.
View SolutionMinimum Size OF mirror required to see full image
View Solution
Knowledge Check
A man of height 1.4 m wishes to see his full image in a plane mirror placed at distance of 2 m . the minimum height of the mirror should be
A0.5 mB0 . 7 mC0 . 9 mDnoneA man of height 1.6 m wishes to see his full image in a plane mirror placed at a distance of 2 m. The minimum length of the mirror should be
A0.4 mB0.8 mC1.6 mD2.4 mA man is standing in a room and a plane mirror is fixed on the wall in fornt of him.The height of the wall is H.Man has to see the complete image of wall behing him at a time
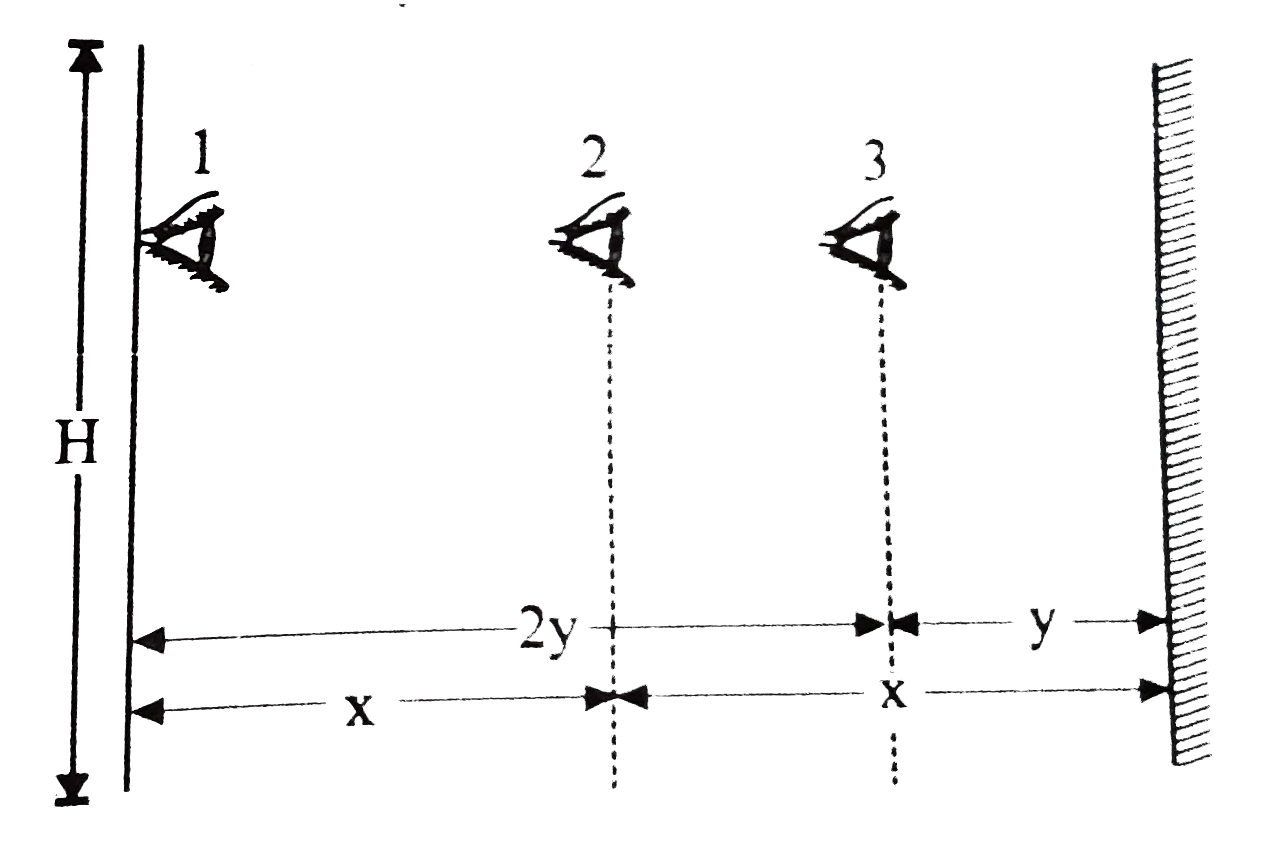
When the man is at position 3,the minimum length of the mirror required isAHBH/2CH/3DH/4
A lady is standing in front of a plane mirror at a distance of
1 m from it. She walks 60 cm towards the mirror. The distance
of her image now from herself (ignoring the thickness of the
mirror) is
View SolutionA man is standing in a room and a plane mirror is fixed on the wall in front of him.The height of the wall is H.Man has to see the complete image of wall behind him at a time

When the man is standing near wall i.e at a position 1,the minimum length of the mirror required is
View SolutionA man is standing in a room and a plane mirror is fixed on the wall in fornt of him.The height of the wall is H.Man has to see the complete image of wall behing him at a time
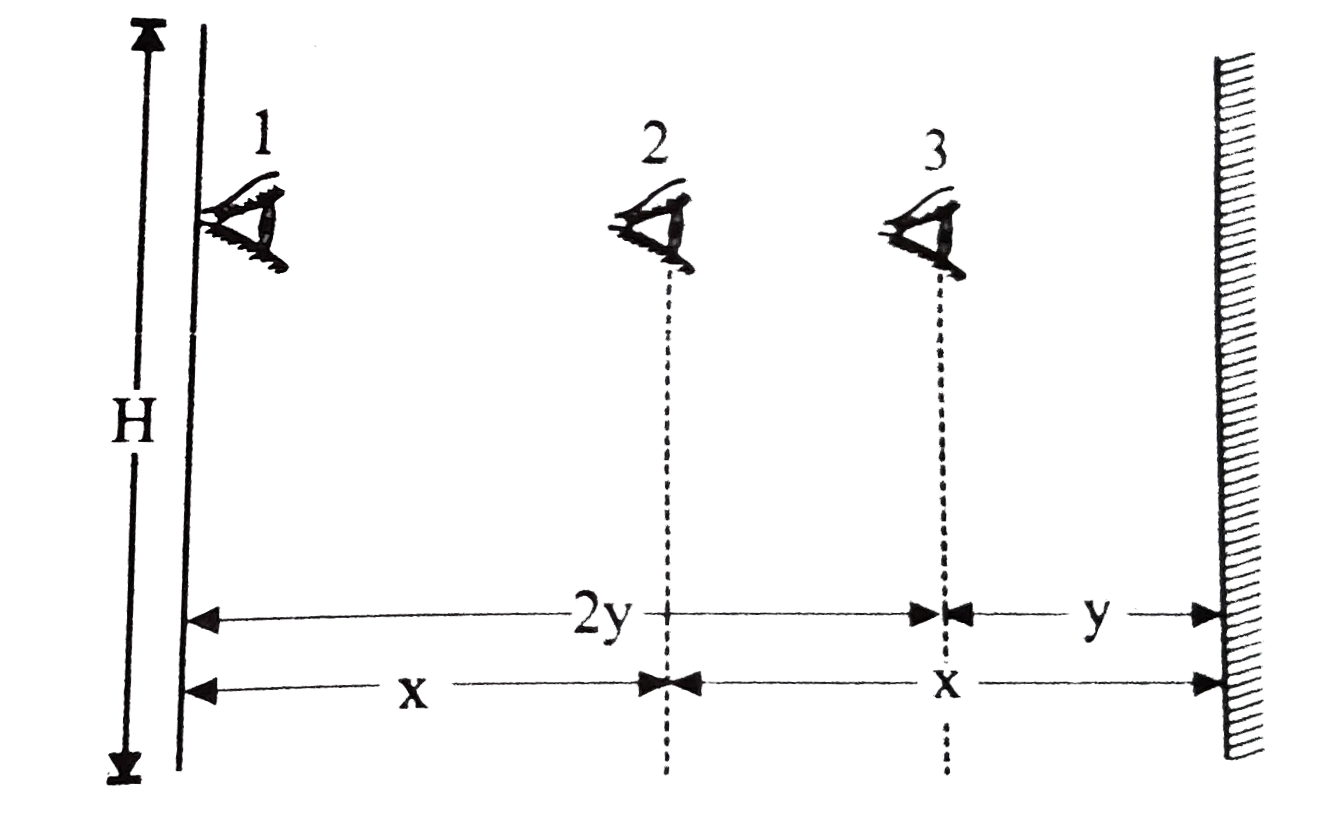
When the man is standing at the midddle of the room i.e at position 2,the minimum length of the mirror required is
View SolutionTwo big mirrors A and B are fitted side by side on a wall. A man is standing at such a distance from the wall that he can see the erect image of his face in both the mirrors. When the man starts walking towards the mirrors, he finds that the size of his face in mirror A goes on increasing but that in mirror B remains the same. Then,
View SolutionTwo bigmirrors A and B are fitted side by side on a wall. A man is standing at such a distance from the wall that he can see the erect image of his face in both the mirrors. When the man starts walking towards the mirrors, he finds that size of his face in mirror A goes on increasing but that in mirror B renaubs the same.
View Solution

