Shown in the Fig. is a spherical surface of radius of curvature R and R.I. . Find the distance of the silvering of the plane surface so as to form an image at the pole due to a very far object.
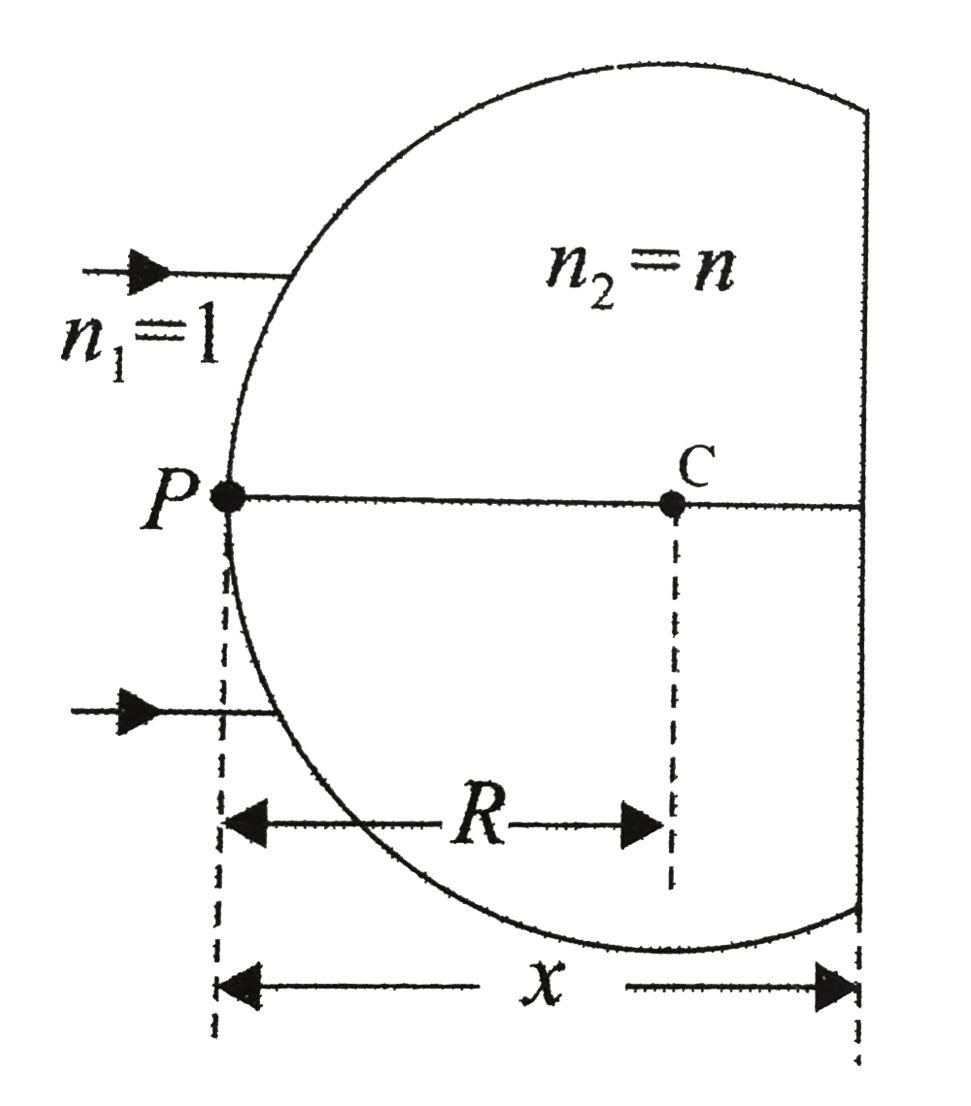
Since light comes from very far object
Due to presence of the plane mirror, the image found at behave as a virtual object for the plane mirror & a real image is formed in front of the plane mirror, at the pole P.

Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Solved Examples
Explore 15 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Exercise1.1
Explore 14 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:QUESTION BANK
Explore 1 Video
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
Similar Questions
Shown in the Fig. is a spherical surface of radius of curvature R and R.I. (=n)1.5. Find the distance of the silvering of the plane surface so as to form an image at the pole due to a very far object.

View SolutionLight from a point source in air falls on a spherical glass surface (n = 1.5 and radius of curvature = 20 cm). The distance of the light source from the glass surface is 100 cm. At what position the image is formed ?
View Solution
Knowledge Check
A denser medium of refractive index 1.5 has a concave surface of radius of curvature 12 cm. An object is situated in the denser medium at a distance of 9 cm from the pole. Locate the image due to refraction in air.
AA real image at 8 cmBA virtual image at 8 cmCA real image at 4.8 cmDA virtual image at 4.8 cmA transparent sphere of radius R and refractie index μ is kept in air. At what distance from the surface of the sphere shold a point object be placed so as to form a rea image at the same distance from the sphere?
AR/μBμRCRμ−1DRμ+1The figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
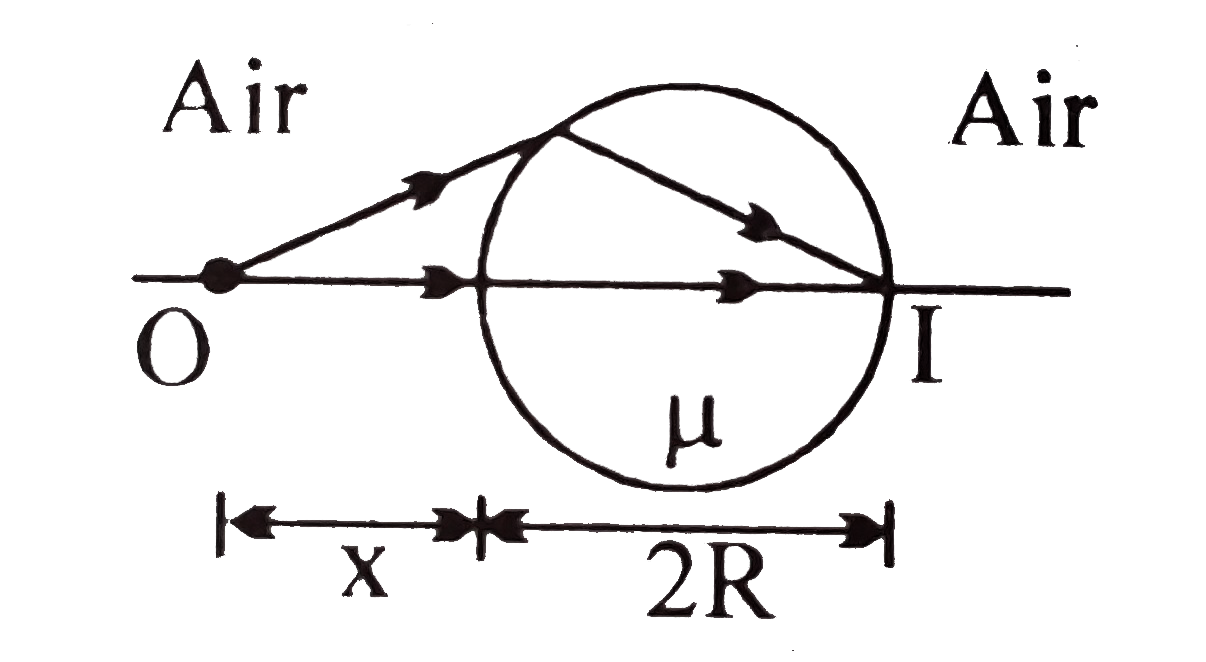 if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byA1.5B2C√2DNone of these
if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byA1.5B2C√2DNone of these
A point object 'O' on the principal axis of a spherical surface of radius of curvature 'R' separating two media of refractive indices n1andn2 forms an image 'I' as shown in the figure below. Prove that n2v−n1v=n2−n1R

View Solution(i) Device the mathematical n between refractive indices n1 and n2 of two radii and radius of curvature R for refraction at a convex shperical surface. Consider the object to be a point since lying on the principal axis in rarer medium of refractive index n1 and a real image formed in the denser medium of refractive index n2. Hence, derive lens marker's formula.
(ii) Light from a point source in air falls on a convex spherical glass surface of refractive index 1.5 and radius of curvature 20cm. The distance of light source from the glass surface is 100cm. At what position is the image formed ?
View SolutionDerive the mathematical relation between refractive indices n1 and n2 of two media and radius of curvature R for refraction at a convex spherical surface. Consider the object to be a point one lying on the principal axis in rarer medium of refractive index nt and a real image formed in the denser medium of refractive index n2. Hence, derive lens maker's formula.
(ii) Light from a point source in air falls on a convex spherical glass surface of refractive index 1.5 and radius of curvature 20 cm. The distance of light source from the glass surface is 100 cm. At what position is the image formed ?
View SolutionThe figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
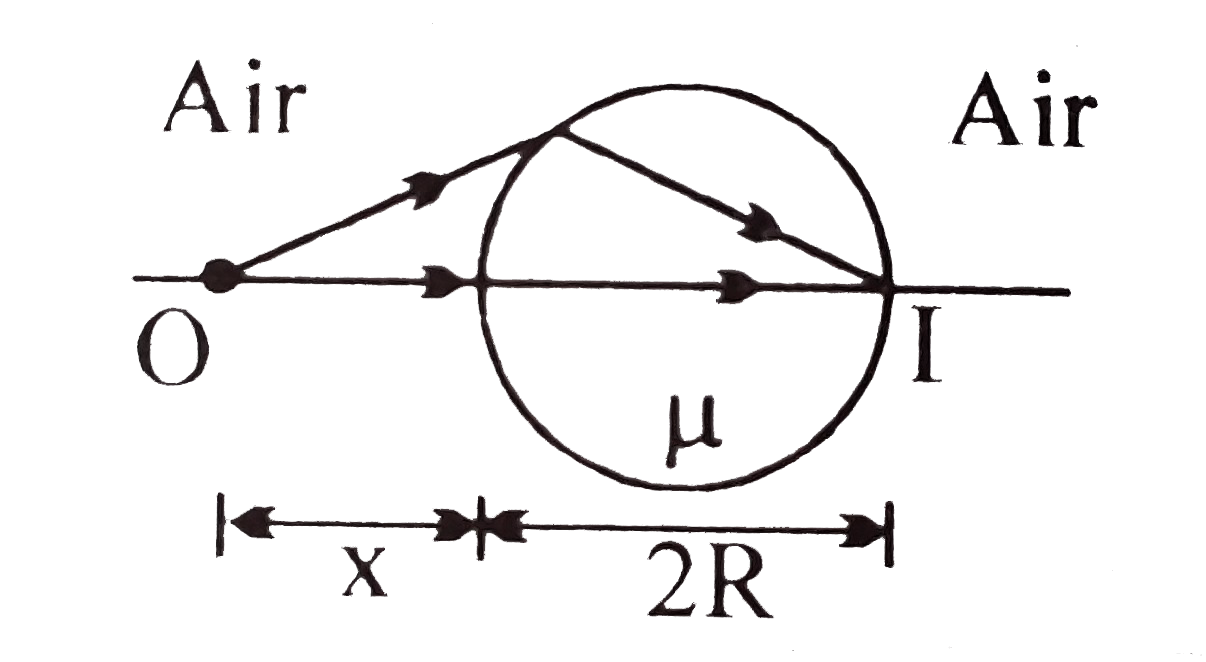
If x=2R,then the value of μis
View SolutionThe figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
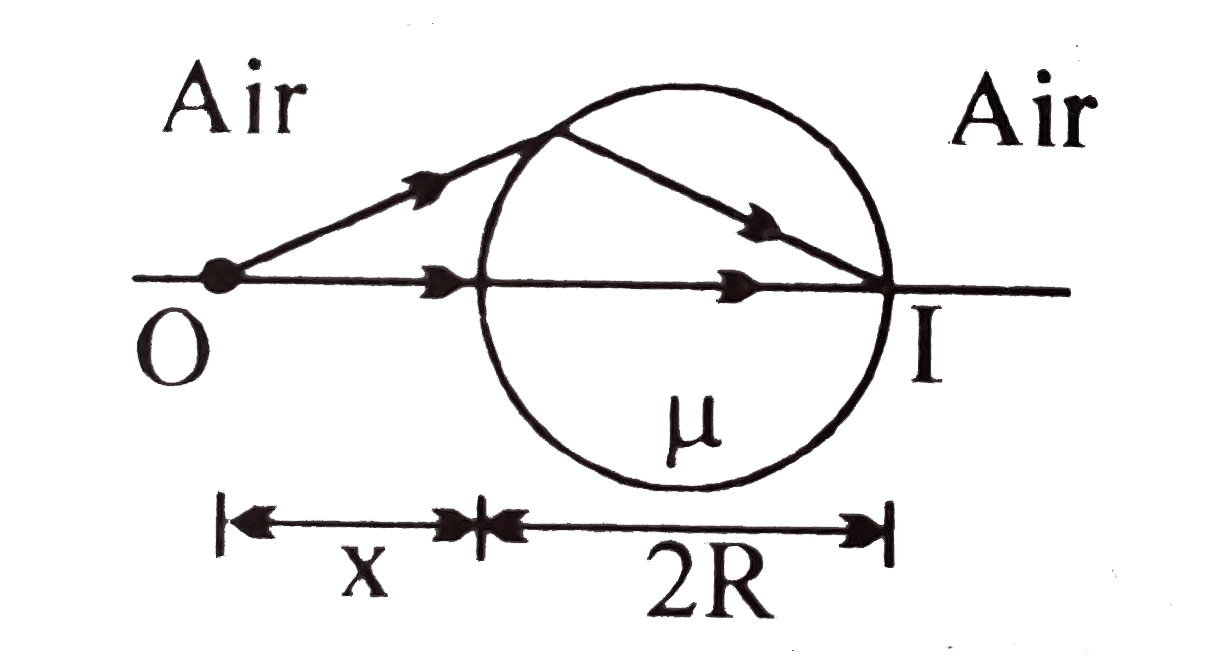 If x=∞,then the value of μ is
If x=∞,then the value of μ is
View Solution