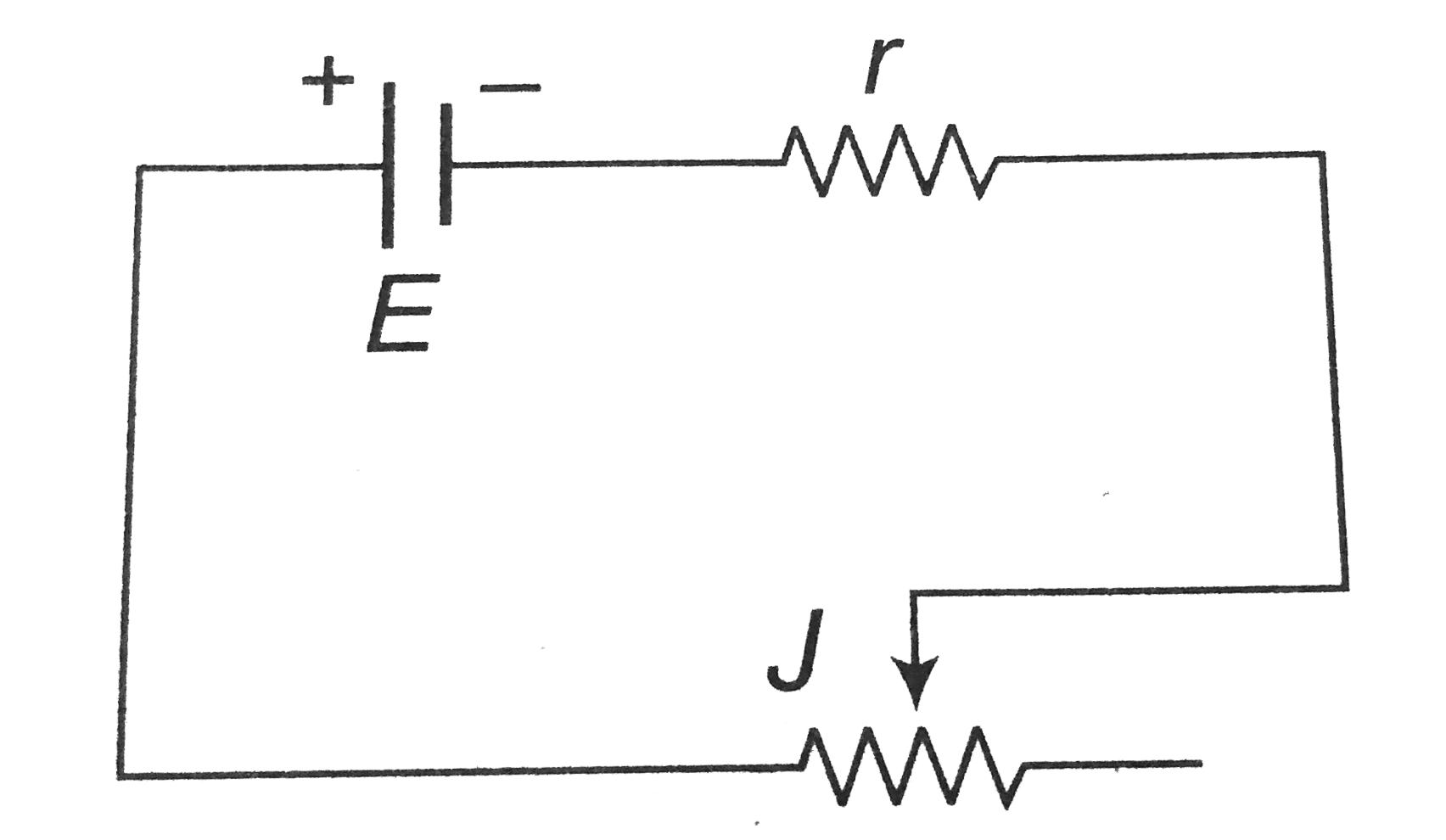
Battery shown in figure has e.m.f. E and internal resistance r. Current in the circuit can be varied by sliding the contact J. If at any instant current flowing through the circuit is I, potential difference between terminals of the cells is V, thermal power generated in the cell is equal to η fraction of total electrical power generated in it, then which of the following graphs is correct ?
A

B
C
D
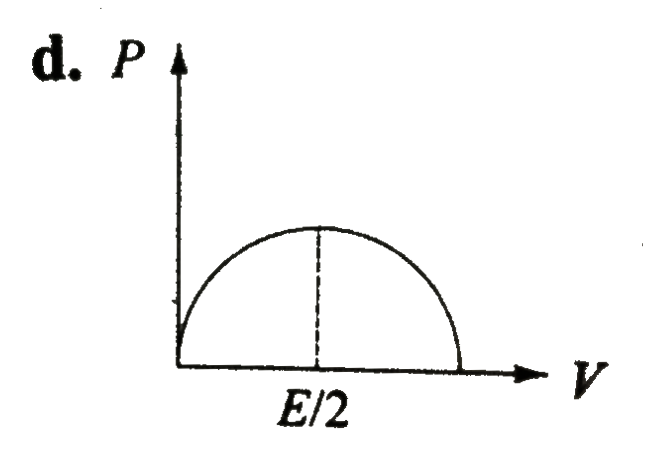
Video Solution
Text Solution
The correct Answer is:A, B, C, D
a., b.,c., d.
Potential difference across the terminals of the cell is given by
V=E−ir. Hence, the graph between V and i will be a straight
line having negative slope and positive intercept. Hence, (a) is
correct.
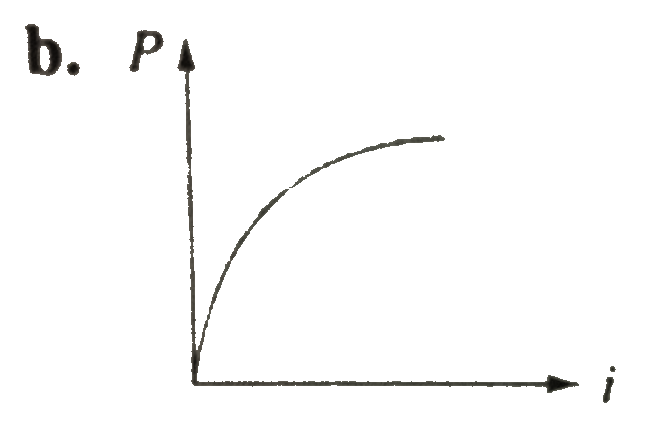
Total electrical power generated is Ei and thermal power
generated in the cell is i2r. Hence, thermal power generated in
the external circuit is P=Ei+i2r. So, the graph between P and
i is a parabola passing through the origin. Hence, choice (b) is
correct.
When terminal potential difference across the cell is V,
current flowing through the circuit will be i=E−V/R and
thermal power generated in the external circuit will be equal to
P=Vi=V(E−Vr)=EVr−V2r
Hence, the graph between P and V will be parabola passing
through the origin and have a maximum value of P at V=E/R.
Hence, choice (d) is correct.
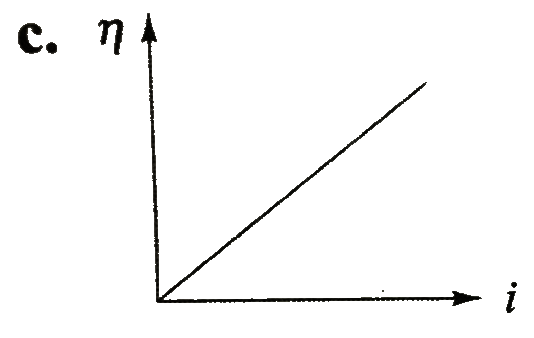
At an instant, thermal power generated in the cell is equal to i2r and total electrical power generated in the cell is equal to
Ei. Hence the fraction η=i2r/Ei=(r/E)i.
Hence, the graph between η and i will be a straight line passing
through the origin and have a positive slope. Hence, (c) is
correct.
|
Similar Questions
Knowledge Check
If internal resistance of cell is negligible, then current flowing through the circuit is
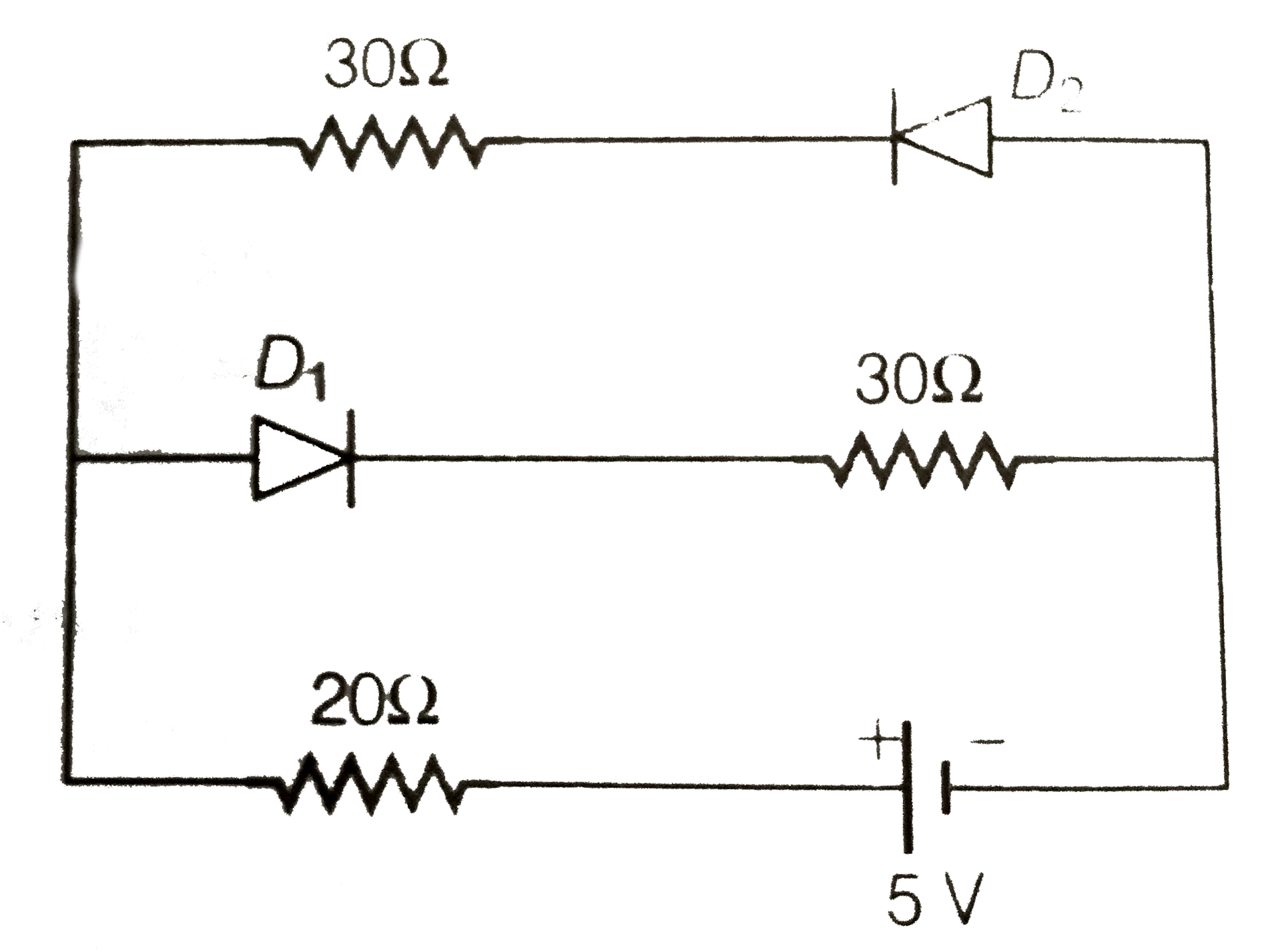 A350AB550AC450AD250A
A350AB550AC450AD250A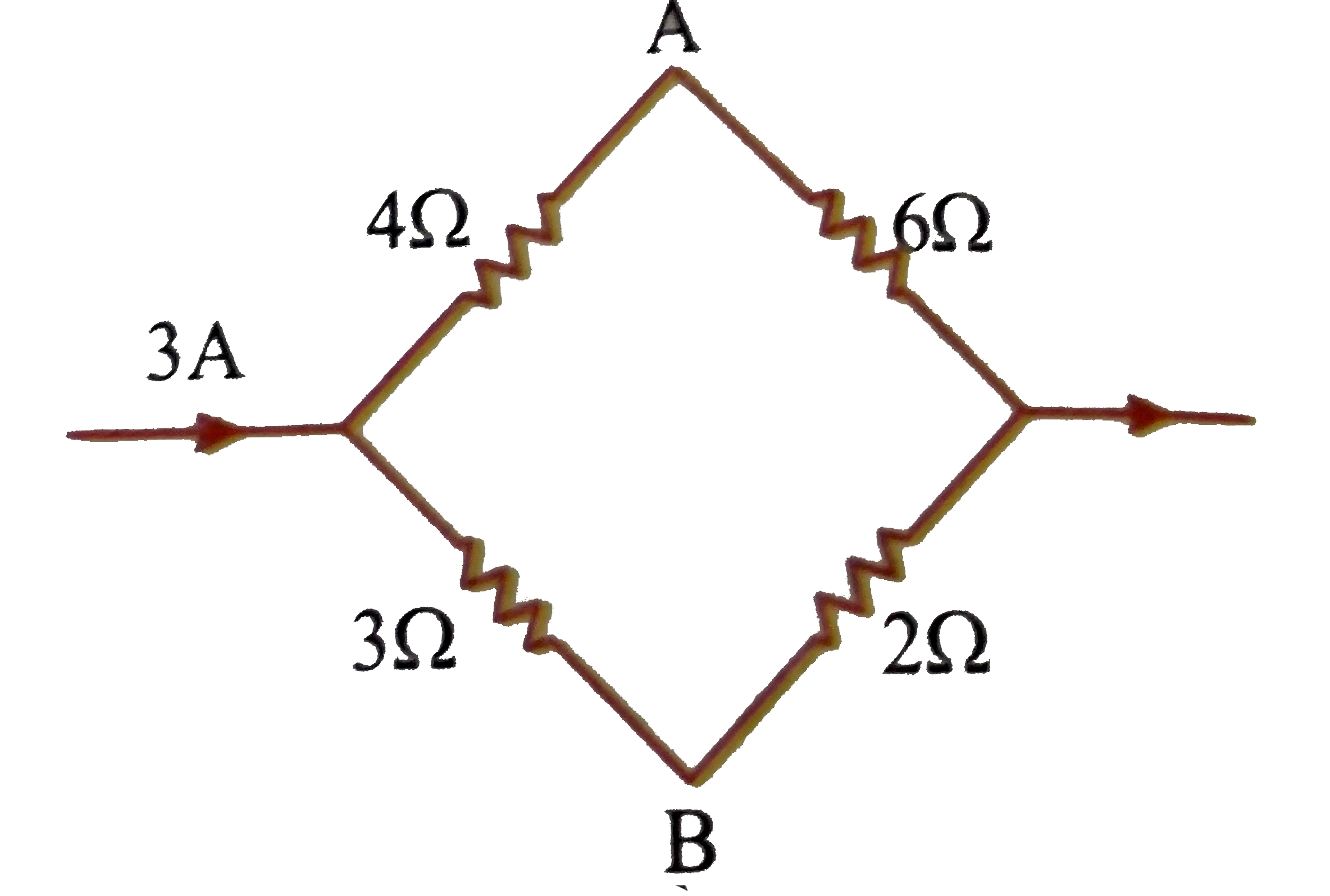
A current of 3A flows in a circuit shown in the figure. The potential difference between A and b isA4VB3VC2VD5VA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
AEBE/2CE/4D3/2
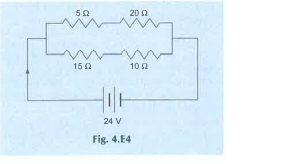
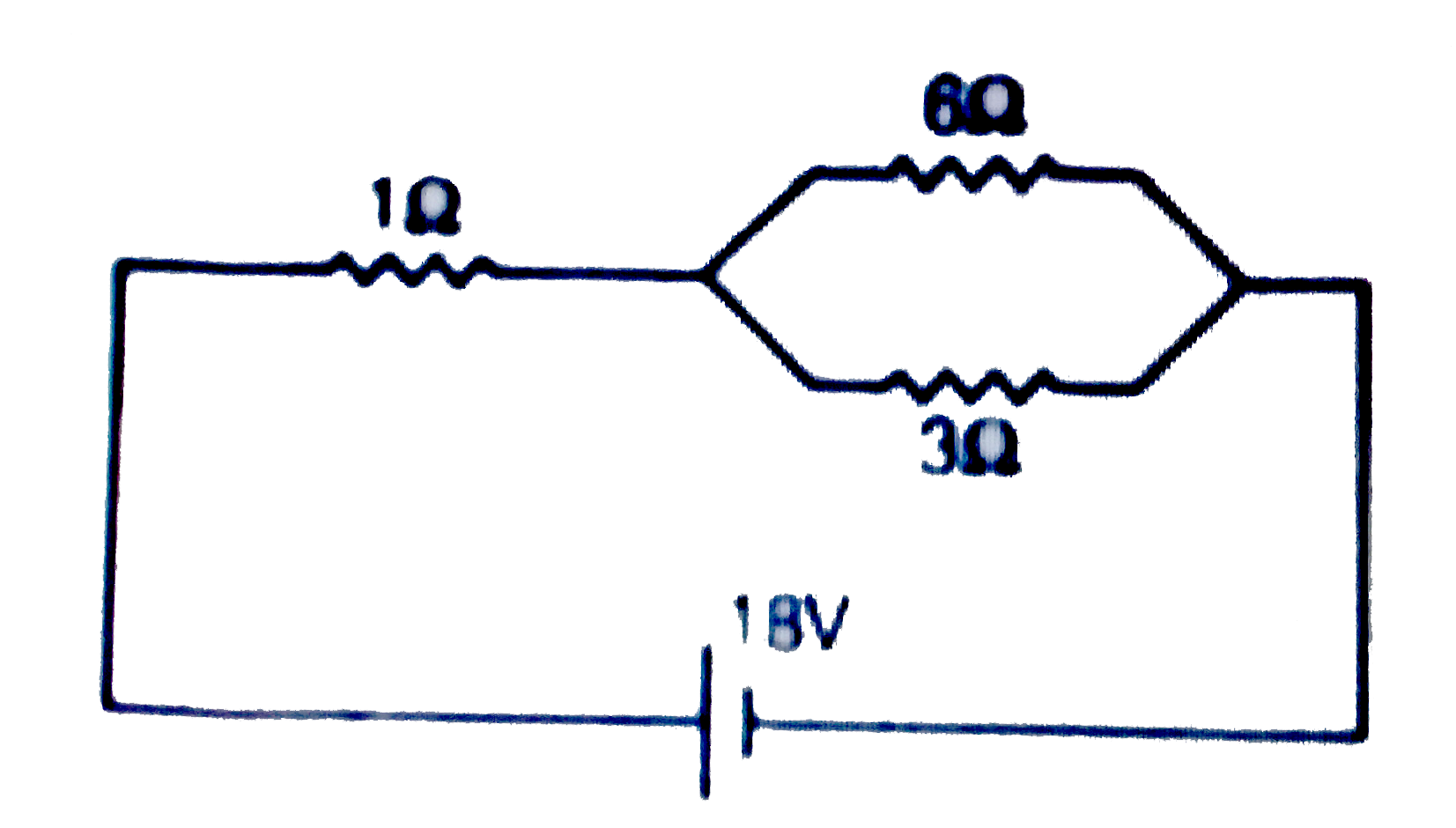
In the circuit shown below, calculate the total resistance of the circuit and the current flowing through it.
View Solution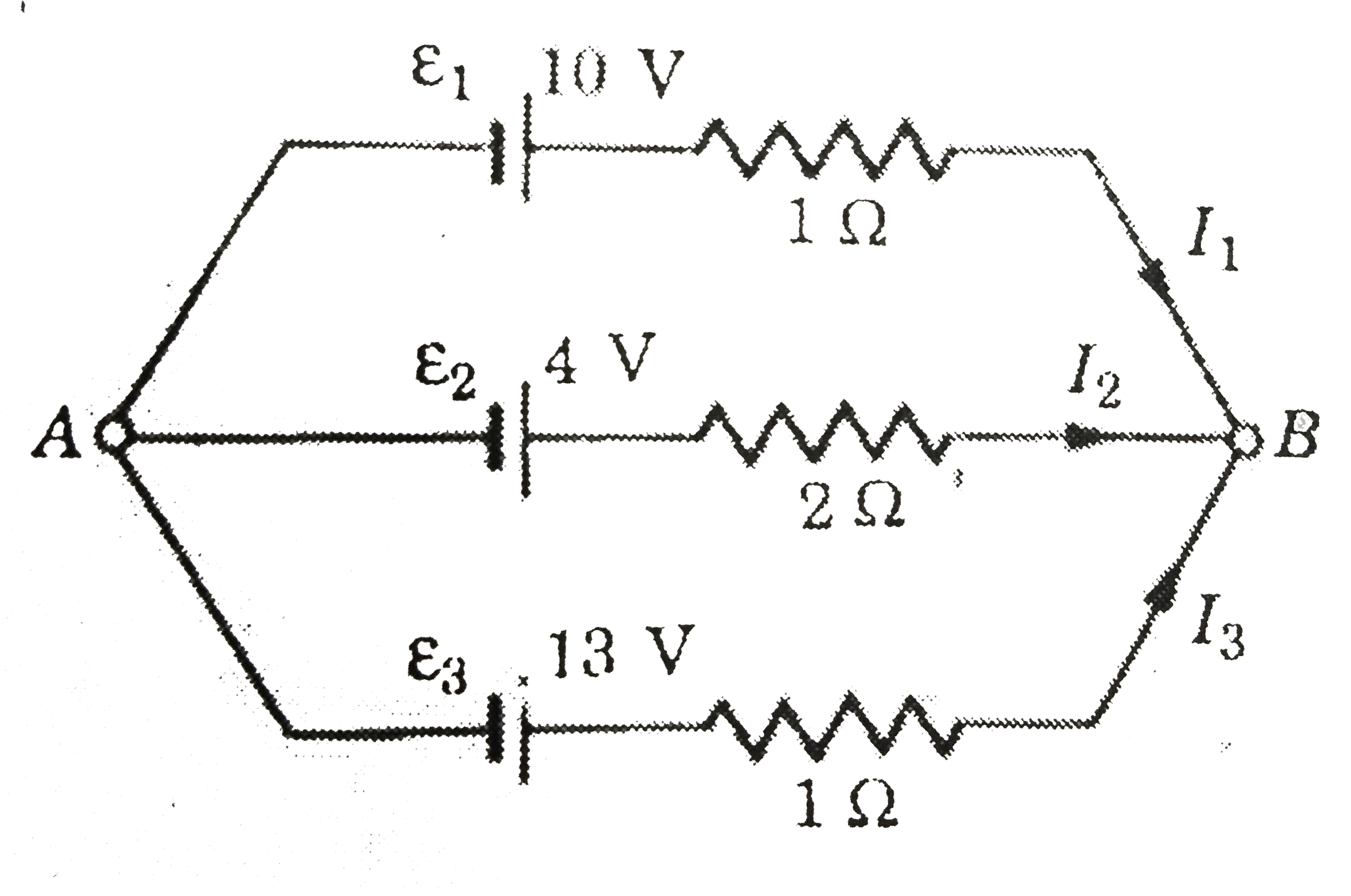
Find the current flowing through each cell in the circuit shown in figure. Also calculate the potential difference across the terminals of each cell.
View SolutionIn the circuit shown in figure, power generated in
View SolutionThe potential difference between the terminals of a cells is found to be 3 volts when it is connected to a resistance equal to its internal resistance. The e.m.f. of the cell is :–
View Solutionv31
View Solution