A spherical symmetric charge system is centered at origin. Given, Electric potential
V=Q4πε0R0(r≤R0), V=Q4πε0r(r>R0)
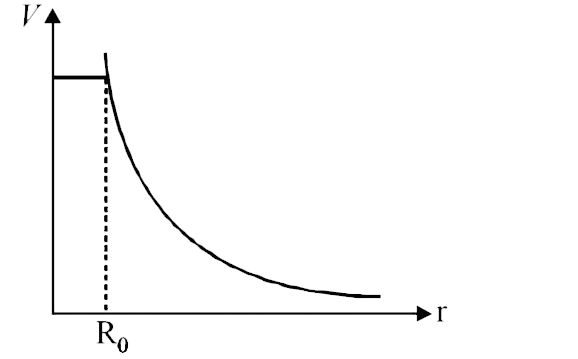
For spherical region r≤R0. Total electrostatic energy stored is zero.
Within r=2R0, total charge is Q.
There will be no charge anywhere except at r=R0 .
Electric field is discontinuous at r=R0 .
For r>R0,E=dϕdr=Q4πε0r2
therefore, charge enclosed by concentric spherical surface at
r is
2R0=ε0ϕE4πr2=ε0Q4πε0r2=Q
For r<R0,E=−dVdr=0
and for r>R0E=−dVdr=4πε0r2 (here V=ϕ)
Similar Questions
For spherical symmetrical charge distribution, variation of electric potential with distance from centre is given in diagram Given that : V=q4πε0R0 for r≤R0andV=q4πε0r for r≥R0
Then which option (s) are correct :
(1) Total charge within 2R0 is q
(2) Total electrosstatic energy for r≤R0 is non-zero
(3) At r=R0 electric field is discontinuous
(4) There will be no charge anywhere except at r<R0

View SolutionFind the dimensional formulae of the following quantities:
(a) the charge Q
(b) the permittivity of free space ε0
(c) the electric field E
(d) the electric potential V
(e) the capacitance C
Q=It, F=l4πε0.q1q2r2,E=Fq,V=Wq=CV
where I: current, F: force,q: charge, r: distance and W: work.
View Solution
Knowledge Check
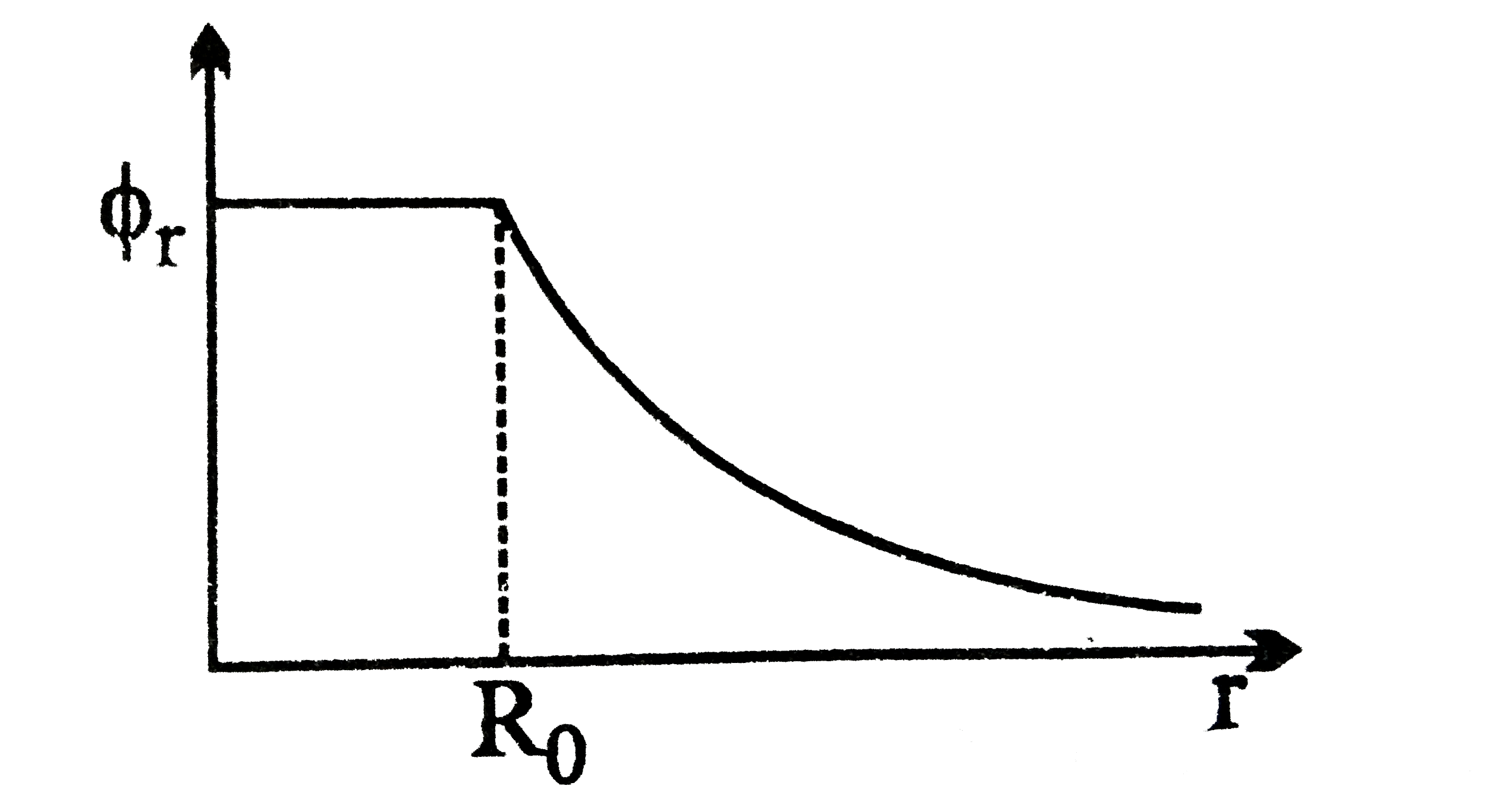
The electrostatic potential ϕr, of a spherical symmetrical system kept at origin, is shown in the adjacent figure, and given as
ϕr=q4πε0r(r≥R0)
ϕr=q4πε0R0(r≤R0)
Which of the following option is incorrect ?
 AFor spherical region r≤R0 total electrostatic energy stored is zeroBWith in r=2R0, total charge is q/2CThere will be no charge anywhere except at r = RDElectric field is discontinuous at r=R0
AFor spherical region r≤R0 total electrostatic energy stored is zeroBWith in r=2R0, total charge is q/2CThere will be no charge anywhere except at r = RDElectric field is discontinuous at r=R0The electrostatic potential (ϕr) of a spherical symmetric system , kept at origin is shown in the adhacent figure, and given as
ϕe=q4πɛ0r(r≤Ro)
ϕe=q4πɛ0Ro(r≤R0)
Which of the following option s in //are correct ?AFor spherical region r≤R0 total electrostatic energy stored id zero .BWithin r=2R0, total charge is q.CThere will be no charge anywhere except at r=R0.DElectric field is discontinuous at r=R0.A charge q=−2.0μC is placed at origin. Find the electric field at (3m,4m,0).
A−(4.32ˆi+5.76ˆj)×102N/CB−(4.32ˆi−5.76ˆj)×102N/CC−(5.76ˆi+4.32ˆj)×102N/CD(4.32ˆi+5.76ˆj)×102N/C
The Bohr model for the H-atom relies on the Coulomb's law of electrostatics . Coulomb's law has not directly been varified for very short distances of the order of angstroms. Suppos-ing Coulomb's law between two oppsite charge +q1,−q2 is modified to ∣∣→F∣∣=q1q2(4πε0)r21r2,r≥R0
=q1q2(4πε0)r21R20(R0r)ε,r≤R0
Calculate in such a case , the ground state enenergy of H-atom , if ε=0.1,R0=1Å
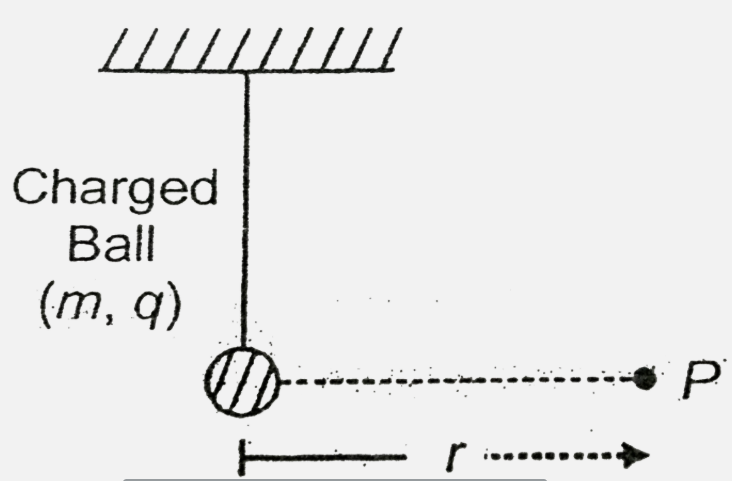
View SolutionThe electric field at point P due to a charged ball is given by
Ep=14πε0qr2
To measure 'E' at point P, A test charge q0 is placed at point P and measure electric force F upon the test charge. Check whether Fq0 is equal to 14πε0qr2 or not .
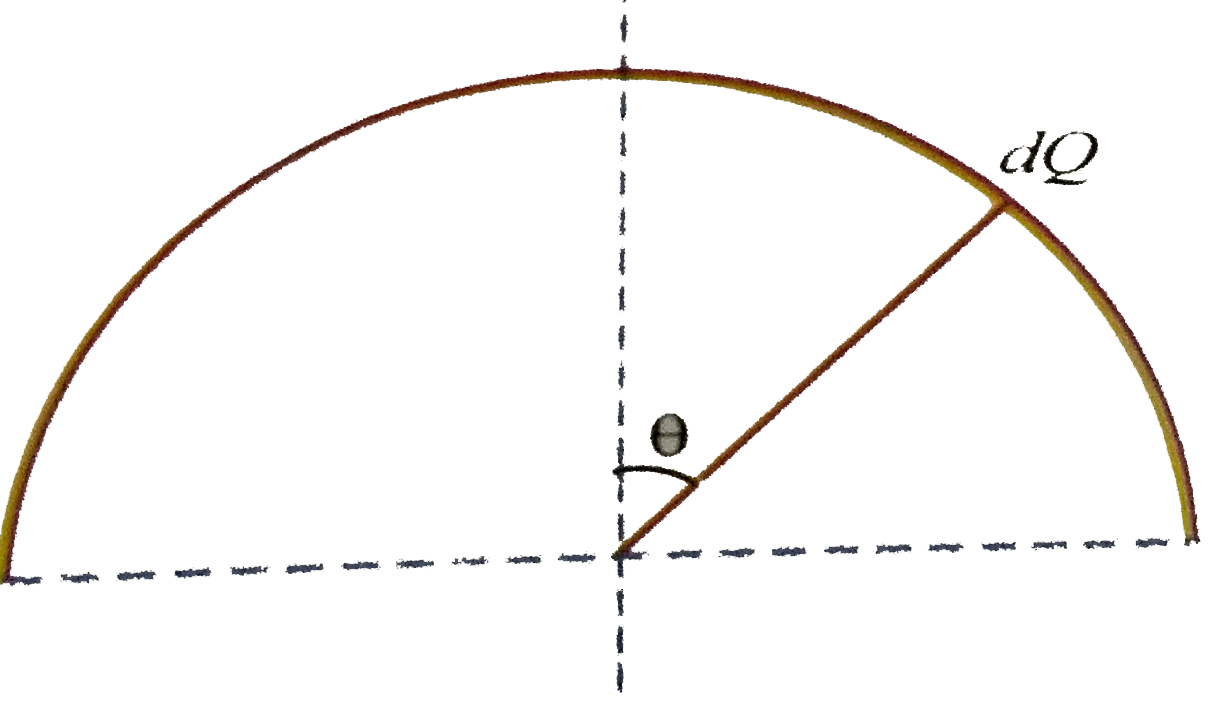
View Solutionthe following diagram represents a semi circular wire of linear charge density λ=λ0sinθ where λ0is a positive constant.The electric potential at o is (take k=14πε0
View SolutionThe Bohr model for the H-atom relies on the Coulomb's law of electrostatics . Coulomb's law has not directly been varified for very short distances of the order of angstroms. Suppos-ing Coulomb's law between two oppsite charge +q1,−q2 is modified to ∣∣→F∣∣=q1q2(4πε0)r21r2,r≥R0
=q1q2(4πε0)r21R20(R0r)ε,r≤R0
Calculate in such a case , the ground state enenergy of H-atom , if ε0.1,R0=1Å
View SolutionA regular hexagon of side a has a charge Q at each vertex. Potential at the centres of hexagon is (k= (14πε0))
View Solution
