A Gausisan surface in the figure is shown by dotted line.
The electric field on the surface will be
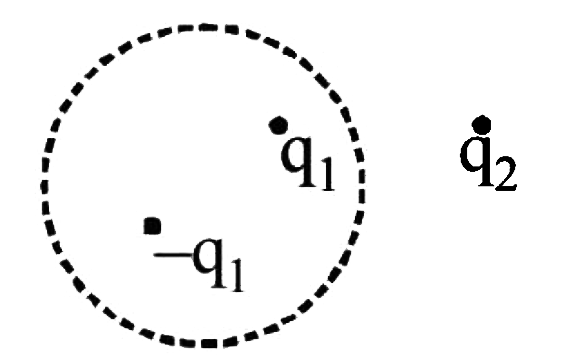
due to q1 and q_2 only
due to q2 only
zero
due to all
The flux through the gaussian surface is due to the charges inside the gaussian surface but the electric field on the gaussian surface will be due to the charges present in the haussian surface and outside it. It wll be due to all the charges.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Multiple Correct Answer type
109 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank
4 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Knowledge Check
A Gaussian surface encloses a proton p. The electric field at any point on the surface is →€. The flux linked with the Gaussian surface is ϕ.
STATEMENT-1 : When an electron is kept close to this system outside the Gaussian surface, the flux linked with the surface would change.
and
STATEMENT-2 : The presence of electron will alterthe electric field on the gaussian surface.AStatement-1 is True, Statement-2 is True, Statement -2 is a correct explanation for Statement-1BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1CStatement-1 is True, Statement -2 is FalseDStatement-1 is False, Statement-2 is True.Consider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
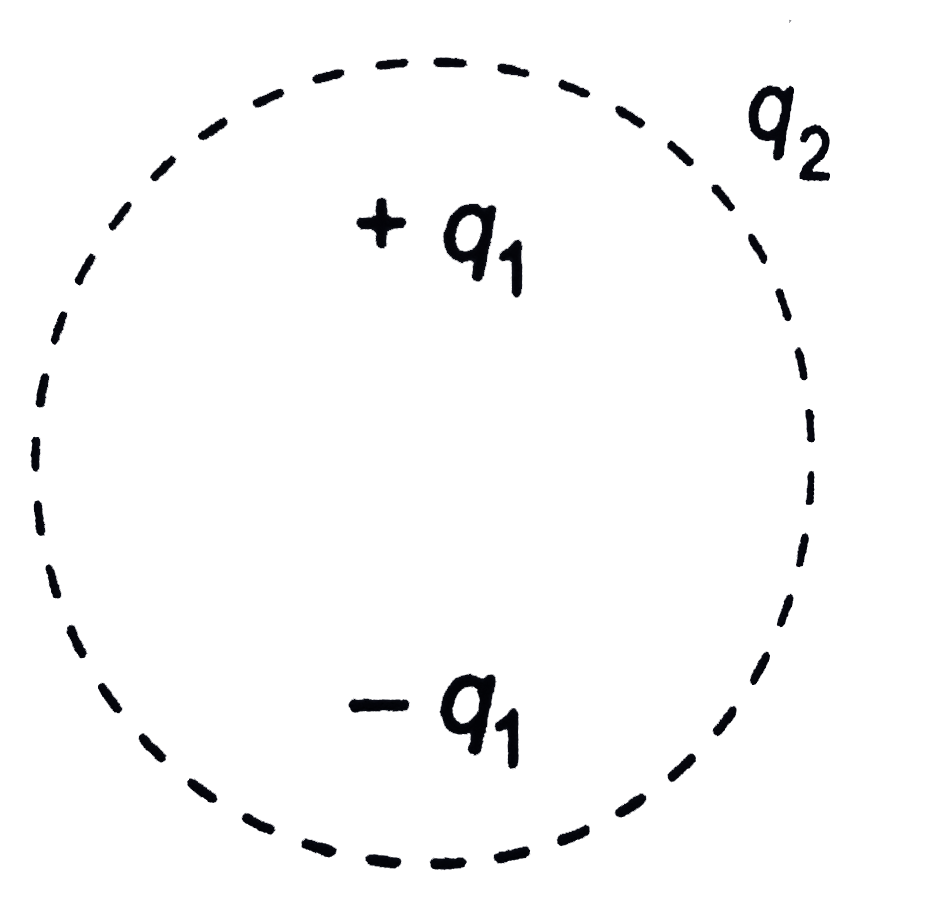 Aq2Bonly the positive chargesCall the chargesD+q1 and −q1
Aq2Bonly the positive chargesCall the chargesD+q1 and −q1If the net electric field flux passing through a closed surface is zero, then the electric field at the surface will be
A0Bsame at all placesCdepends upon the location of pointsDinfinite
If the total charge enclosed by a surface is zero, does it imply that the electric field everywhere on the surface is zero ? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
View SolutionSome equipotential surface are shown in the figure. Find the value of electric field :-

View SolutionThe black shapes in the figure below are closed surfaces. The electric field lines are in red. For which case the net flux through the surfaces is non-zero ?

View SolutionA spherical charged conductor has σ as the surface density of charge. The electric field on its surface is E. If the radius of the sphere is doubled keeping the surface density of charge unchanged, what will be the electric field on the surface of the new sphere -
View SolutionThe surface density on a copper sphere is σ. The electric field strength on the surface of the sphere is
View Solution
