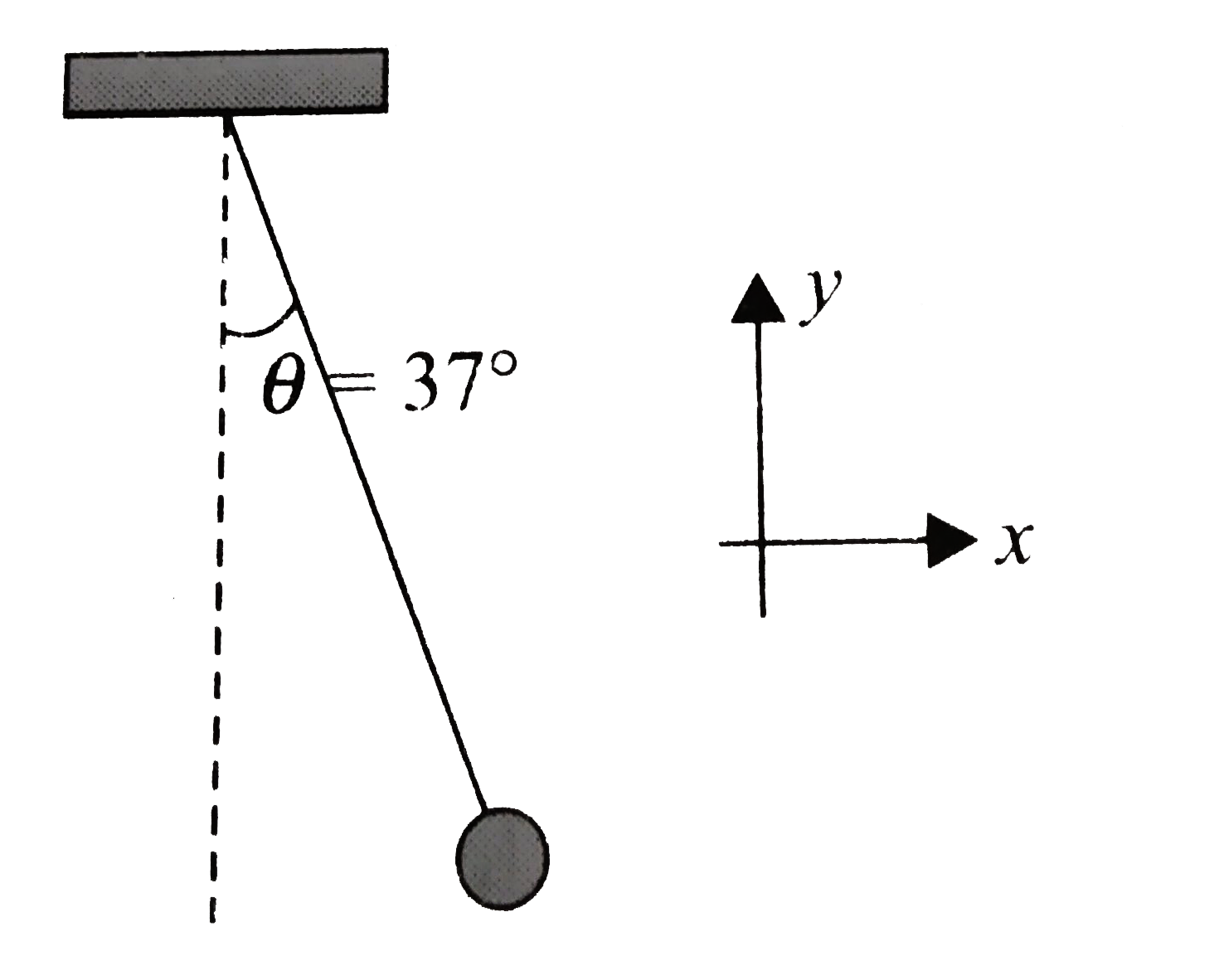
A charged ball of mass 9 kg is suspended from a string in a uniform electric field →E=(3ˆi+5ˆj)×105N/C. The ball is in equilibrium with θ=37∘. If direction of electric field is reversed, find the new equilibrium position of the ball. Given your answer in terms of angle made by string with vertical. Take g=10ms−2.
tan−1(34)
cot−1(314)
cot−1(34)
tan−1(314)
The correct Answer is:D
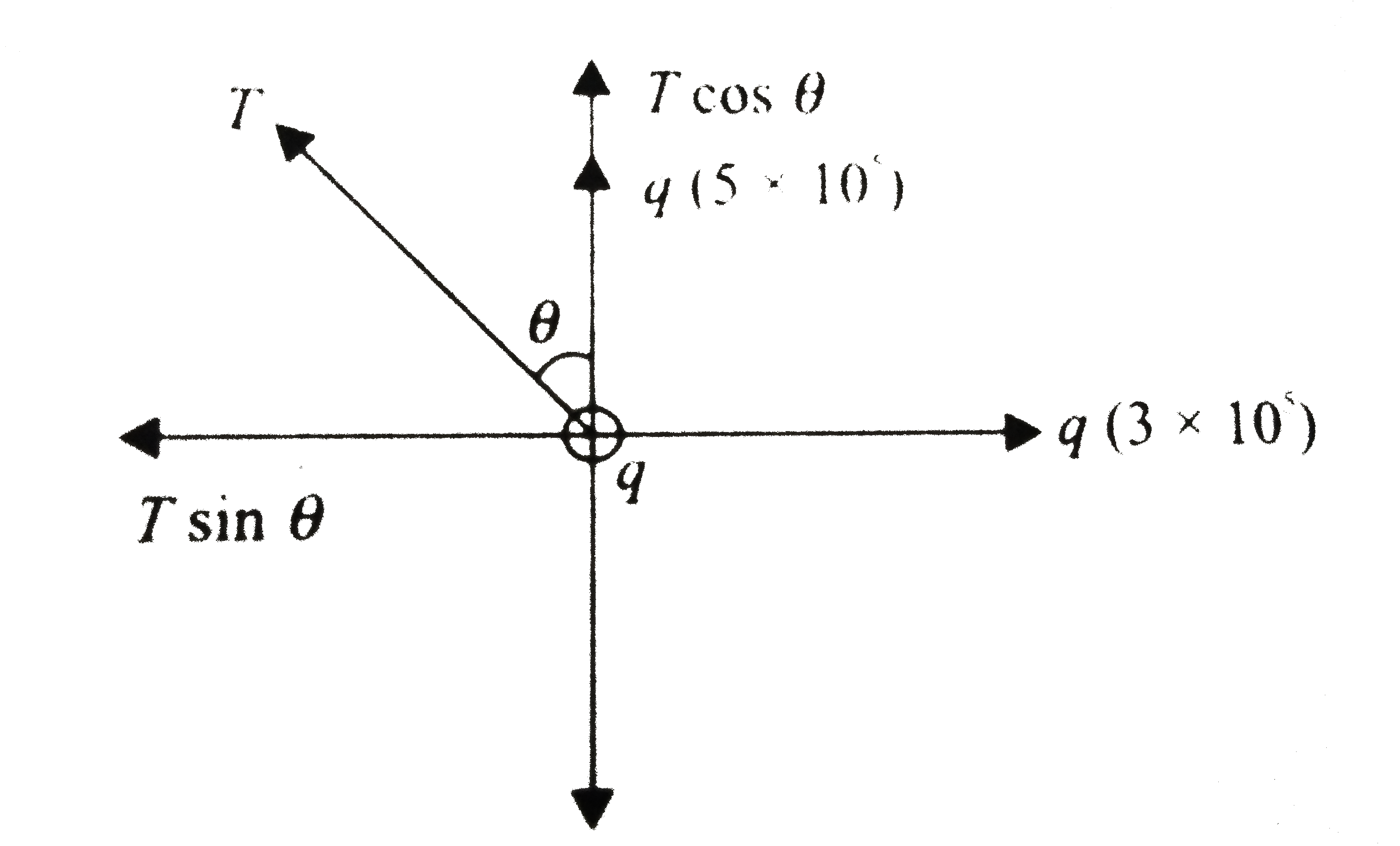
Tsinθ=3θ×105 (i)
Tcosθ=mg−5q×105 (ii)
Solve to get q=100μC,T=50N.
After the rever4sal of direction of electric field

T'sina=3q×105 or T'cosa=mg+5q×105)
tana=(3q×105)
=3×10−4×1059×10+5×10−4×105=314
or a=tan−1(314)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Multiple Correct Answer type109videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank4videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
A charged cork ball of mass m = 16 g is suspended from a light string in the presence of a uniform electric field as shown in the figure. When E=(12ˆi+2ˆj)N/C , the ball is in equiligrium at the angle of 37∘. find W if
The charge on the ball is W×10−2C.View SolutionA charged cork ball of mass m = 16 g is suspended from a light string in the presence of a uniform electric field as shown in the figure. When E=(12ˆi+2ˆj)N/C , the ball is in equiligrium at the angle of 37∘. find W if
The tension in the string is W×10−2N.View Solution
Knowledge Check
- Question 1 - Select One
A charged ball of mass 9 kg is suspended from a string in a uniform electric field →E=(3ˆi+5ˆj)×105N/C. The ball is in equilibrium with θ=37∘. If direction of electric field is reversed, find the new equilibrium position of the ball. Given your answer in terms of angle made by string with vertical. Take g=10ms−2.
 Atan−1(34)Bcot−1(314)Ccot−1(34)Dtan−1(314)
Atan−1(34)Bcot−1(314)Ccot−1(34)Dtan−1(314) - Question 2 - Select One or More
A charged cork of mass m suspended by a light string is placed in uniform electric field filed of strength E=(ˆi+ˆj)×105NC−1 as shown in the figure. If in equilibrium position tension in the string is 2mg/(1+√3) the angle α with the vertical can be
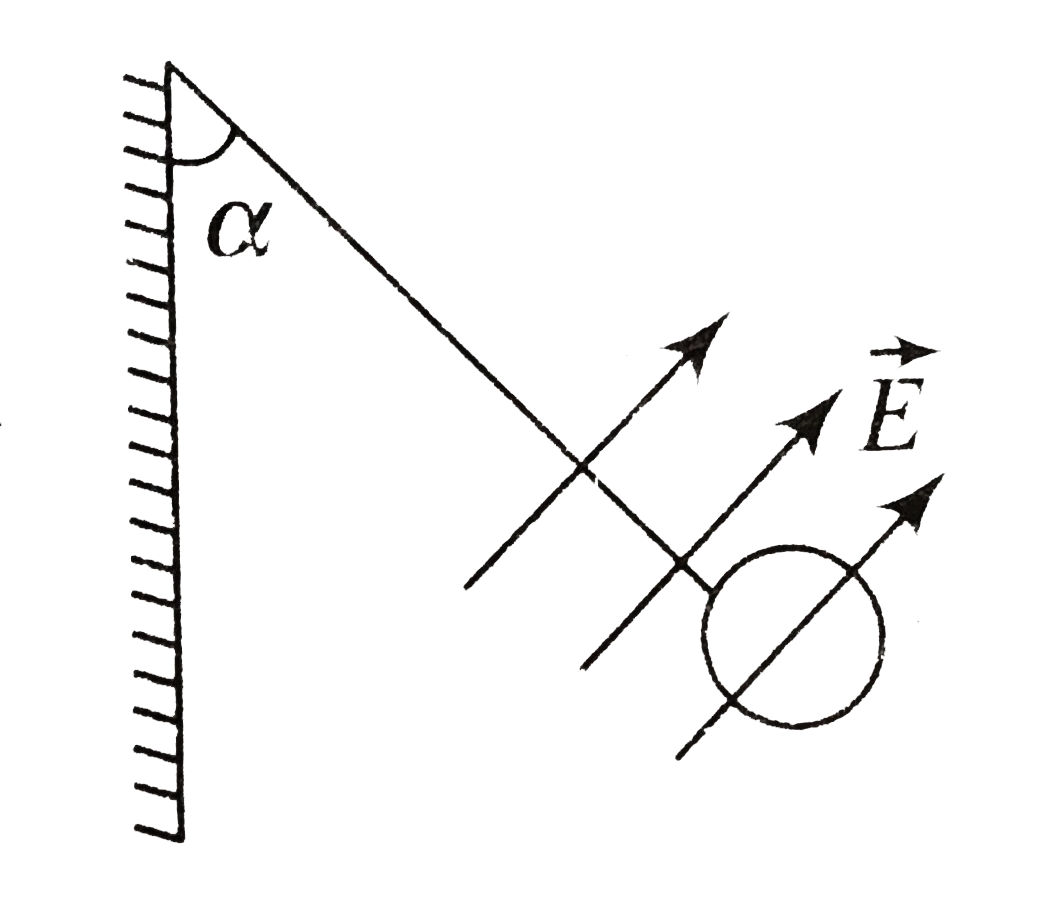 A60∘B30∘C45∘D18∘
A60∘B30∘C45∘D18∘ - Question 3 - Select One or More
A charges cork of mass m suspended by a light stright is placed in uniform electric field strength E=(ˆi+ˆj)×105NC−1 as shown in the figure. If in equilibrium position tension in the string is 2mg(1+√3) then angle 'α' with the vertical is:
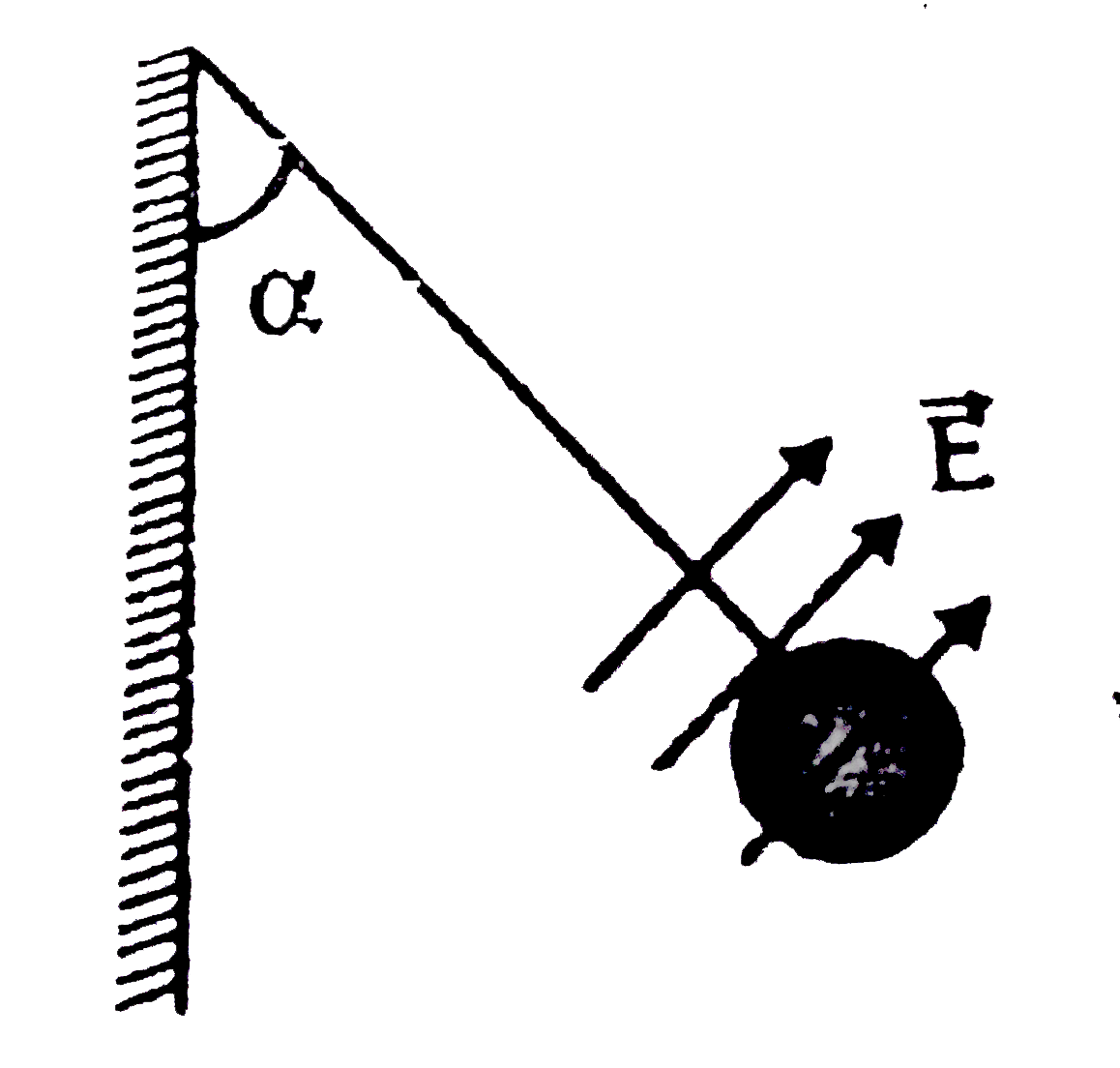 A60∘B30∘C45∘D18∘
A60∘B30∘C45∘D18∘
A charged cork ball of mass m is suspended on a light sting in the presence of a uniform electric field as shown in fig. When E=(Aˆi+Bˆj)NC−1, Where A and B positive numbers, the ball is in equilibirum at θ. Find (a) the charge on the ball and (b) the tension in the string.
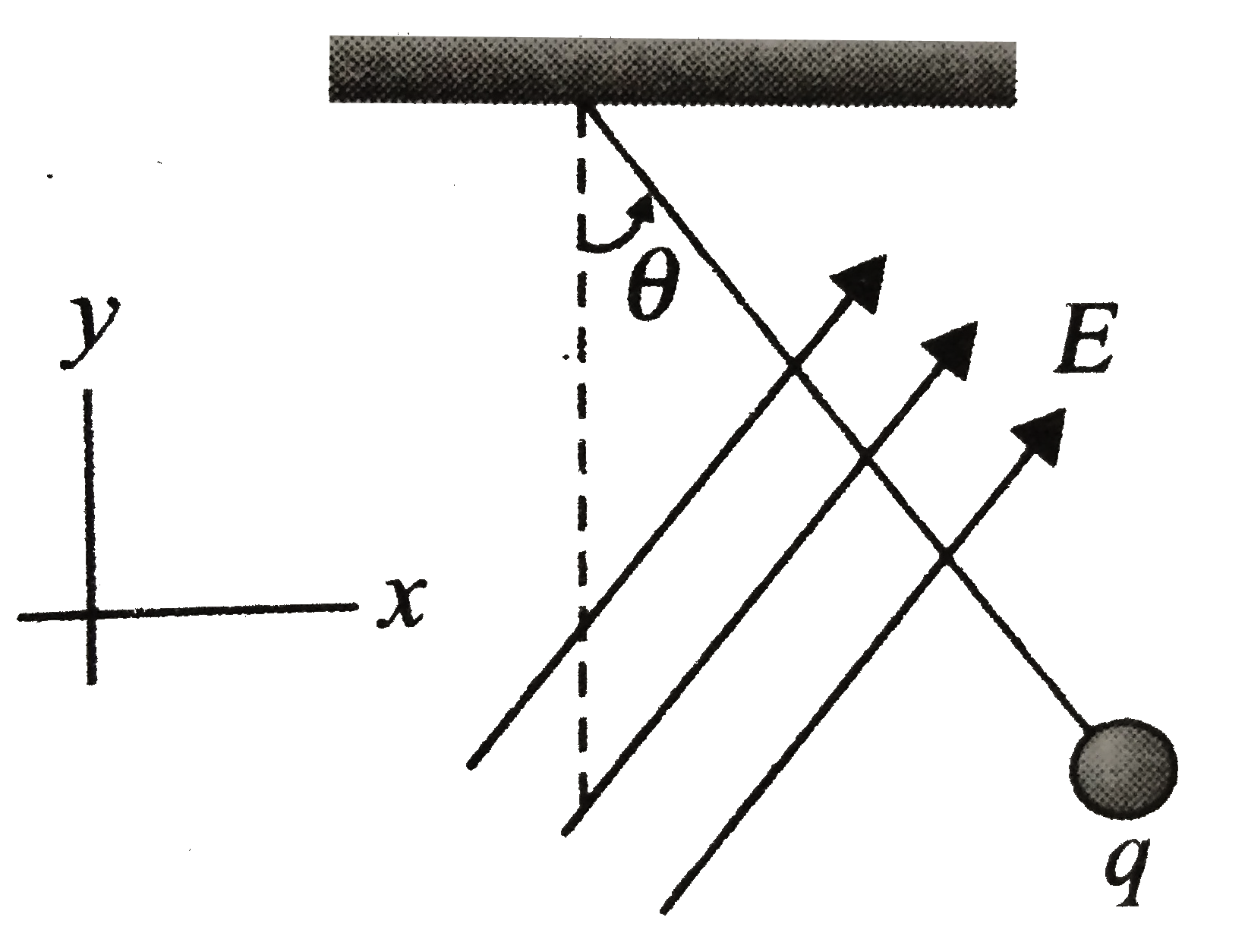 View Solution
View SolutionA charged ball of mass 8.4×1016kg is found to remain suspended in a uniform electric field of 2×104Vm−1. Calculate the charge on the ball. Given g=10m/s2
View SolutionA small ball of mass m and charge q is suspended through a string in uniform electric field E applied in horizontal direction. How much tension would be developed in the string if it stays in equilibrium?
View Solutioncalculate the time taken by a spherical ball if the direction of electric field is reversed and the charge on the particle is changed to +3.5×10−19 C
View SolutionA mass m carrying a charge q si suspended form a string and placed in a uniform horizontal electric field of intensity E.The angel made by the string with the vertical in the equilibrium position is
View Solution

