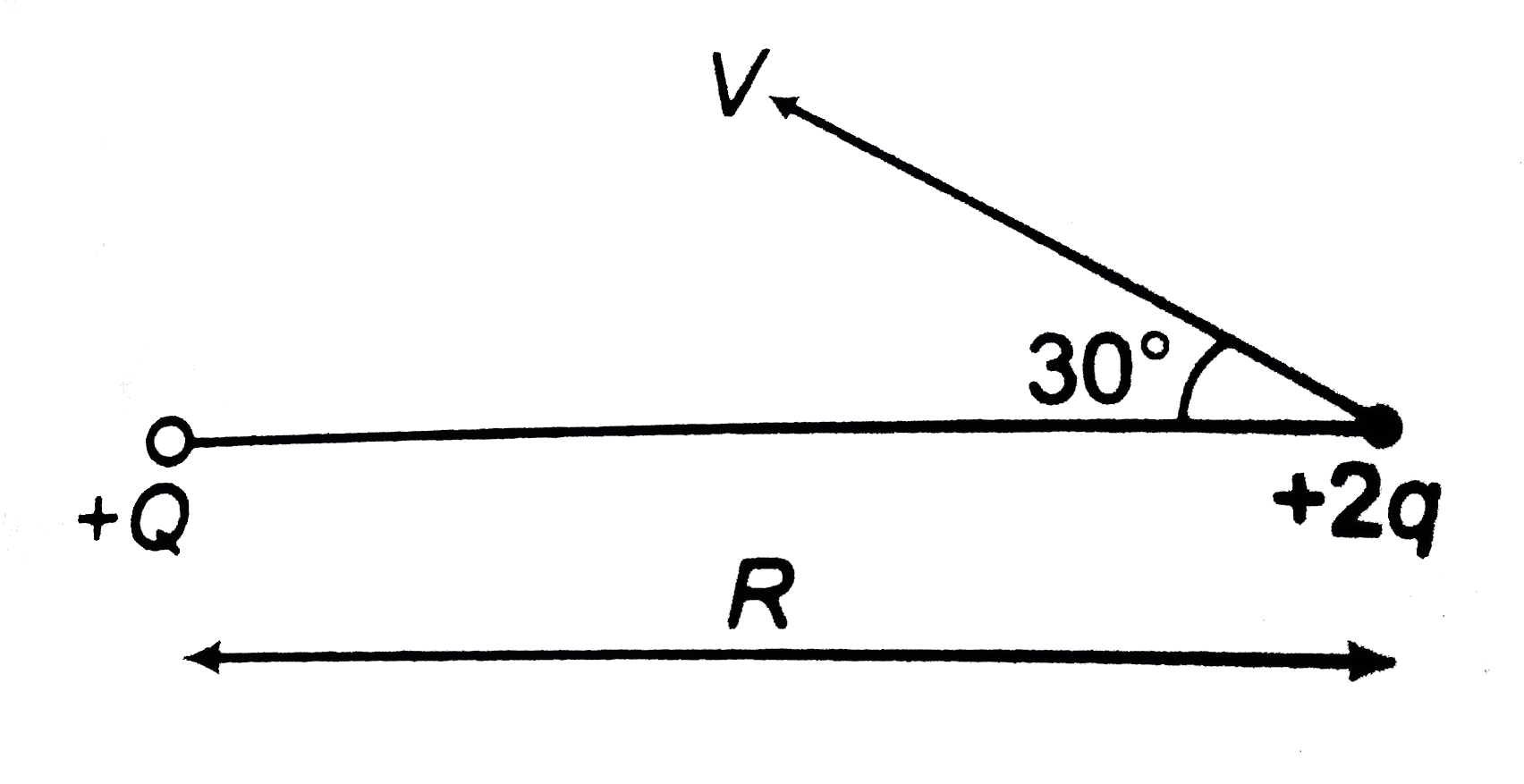
In the diagram shown the charge +Q is fixed. Another charge +2q and mass M is projected from a distance R from the fixed charge. Minimum separtion between the two charge if the velocity becomes 1√3 time of the projected velocity, at this moment is (Assume gravity to be absent)
√32R
√3R
12R
4R
The correct Answer is:A
Using conservation of angular momentum about fixed charged, we have
(mvsin30∘)R=mv1r or v2R=v√3r
or r=√32R

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Multiple Correct Answer type109videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank4videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
A particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View Solution
Knowledge Check
- Question 1 - Select One
A charge q of mass m is projected form a long distance with speed v towards another stationery particle of same mass and charge the distance of closet approach of the particles is
Aq22πε0mv2B2q2πε0mv2C3q22πε0mv2Dq2πε0mv2 - Question 2 - Select One
A particle of charge −q and mass m moves in a circular orbits of radius r about a fixed charge +Q.The relation between the radius of the orbit r and the time period T is
Ar=Qq16π2ε0MT3Br3=Qq16π2ε0MT2Cr2=Qq16π3ε0mT3Dr2=Qq16π3ε0mT3 - Question 3 - Select One
A particle is projected from the mid-point of the line joining two fixed particles each of mass m. If the separation between the fixed particles is l, the minimum velocity of projection of the particle so as to escape is equal to
A√GMlB√GM2lC√2GMlD2√2GMl
Assume that a point charge q is projected from a large distance toward the center of a fixed charged ring along its axis. What should be its initial velocity so that the charge may reach the other side of infinity?
View SolutionA point charge of charge -q and mass m is released with negligible speed from a distance √3R on the axis of a fixed uniformly charged ring of charge Q and radius R. Find out its velocity when it reaches it reaches at the centre of the ring.
 View Solution
View SolutionTwo point charges, each of mass m and charge q are released when they are at a distance from each other. What is the speed of each charged particle when they are at a distance 2r ?
View SolutionA ball of mass of 1 kg and charge 50μC is directly projected from infinity toward another fixed ball of charge 1/6μC ( as shown in Fig. 24-5). The initial velocity of projection is 10 m/s. Find the distance and its velocity at the closest separation. Assume that the initial line of motion is at a distance of 1 m from the second fixed charge.
View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
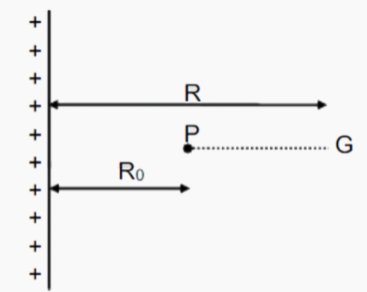 View Solution
View Solution

