Consider the situation shown in figure. We find electric field E at point P using Gauss's law and it comes out to be $E = σ / ε_{0}$ . This electric field is due to

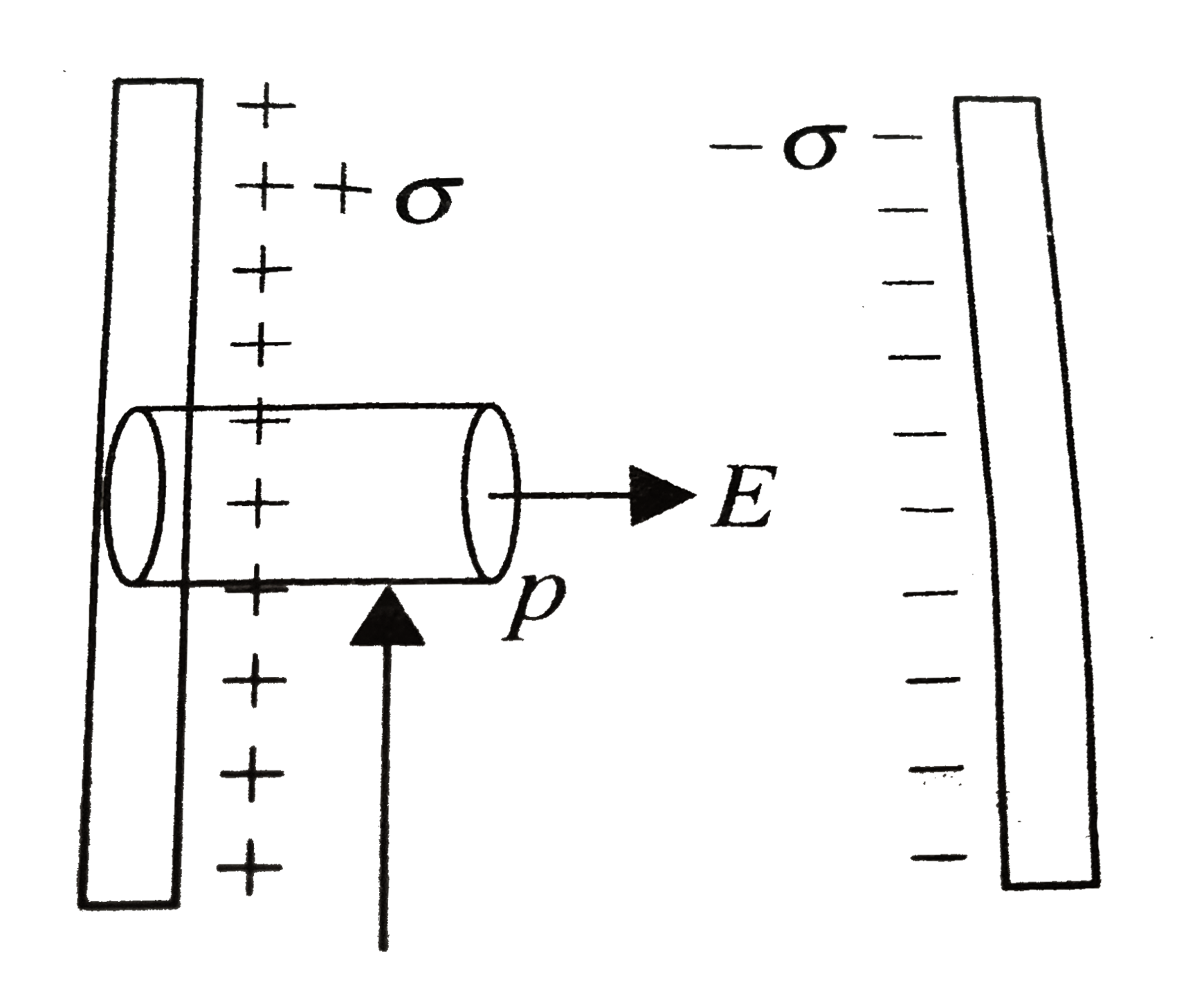
all the amount of charges present on both the plates

all the charges present on positive plate only

positive charge present only inside the Gaussian surface.

positive charge present inside the Gaussian surface plus equal magnitude of negative charge present on negatice plate in front of Gaussian surface.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Consider the situation when an electric field E is present in a conductor. Acceleration a of the free electrons of the conductor due to this field is
A $a = \frac{e E}{m}$
B $a = \frac{e}{E m}$
C $a = \frac{E}{e m}$
D $a = \frac{- e E}{m}$
Figure shows the electric field lines around an electric dipole. Which of the arrows best represents the electric field at point P ?

A
B
C
D