A capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit

A

changes with time

B

does not change with time and it is equal to time constant of circuit

C

does not change with time, but not equal to time constant of circuit

D

may or may not change depending upon the charge given to the capacitor

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Charge on capacitor at any time is
$q = Q E^{- t / τ}$ (i)
Differentating Eq. (i) with respect to time, we get the current
$I = \frac{d q}{d t} = \frac{Q}{τ} e^{- t / τ}$ (ii)
Required ratio is $q / I = τ$ [by diciding Eq. (i) by Eq.(ii)]

|

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A capacitor of capacitance $5 μ F$ is charged to a potential difference 200 V and then allowed to dischage through a resistance $1 k Ω$ . The cahrge on the capacitor at the instant the current through the resistance is 100 Ma, is (in $μ C$ ):
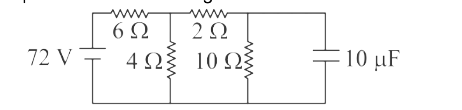
A50
B100
C500
D1000
Question 2 - Select One
Find the charge on the capacitor in the following circuit.

A $12 μ C$
B $14 μ C$
C $20 μ C$
D $18 μ C$
Question 3 - Select One or More
When a capacitor discharges through a resistance $R$ , the time constant is $τ$ and the maximum current in the circuit is $i_{0}$
AThe initial charge on the capacitor was $i_{0} τ$
BThe initial charge on the capacitor was $\frac{1}{2} i_{0} τ$
CThe initial energy stored in the capacitor was $i_{0}^{2} τ$
DThe initial energy stored in the capacitor was $\frac{1}{2} i_{0}^{2} R τ$

CENGAGE PHYSICS-ELECTRIC CURRENT AND CIRCUIT-Single Correct

Home
Ask Doubt
Profile