Figure 5.260 shows two square, X and Y cut from a sheet of metal of uniform thickness t. X and Y have sides of length L and 2L, respectively.
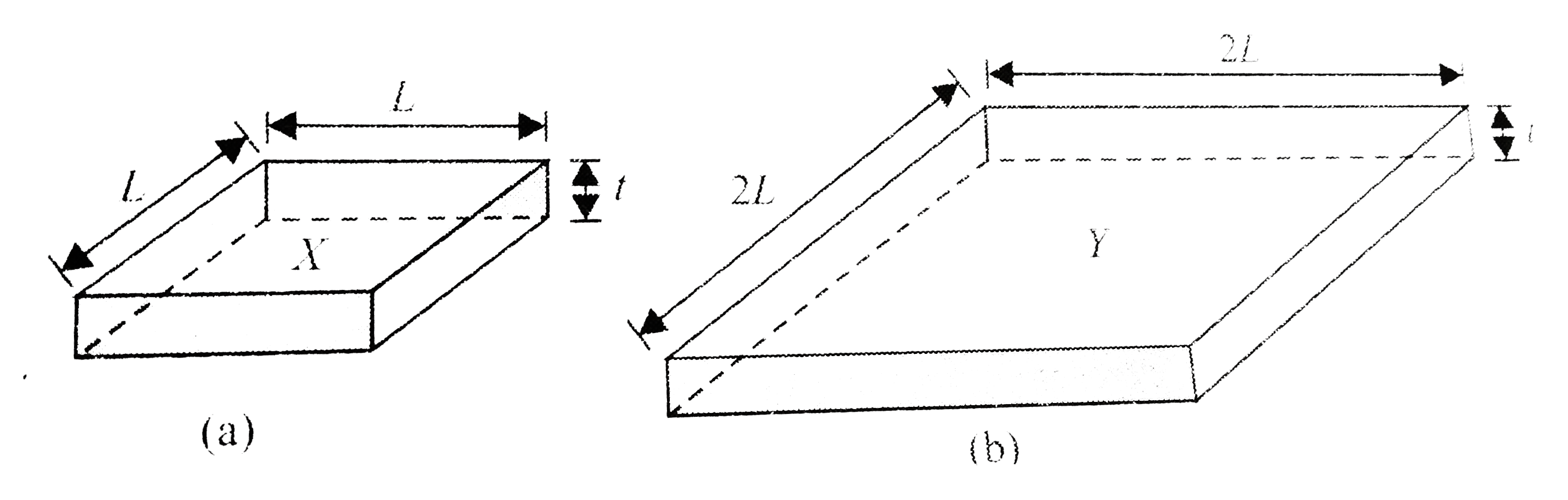
The resistances RxandRy of the squares are measured between the opposite faces shaded in fig. What is the value of Rx/Ry?
1/4
1/2
1
2
The correct Answer is:C
The resistance of the square X is given by
Rx=ρLLt=ρt
where ρ is the resistivity on the metal. Similarly,
RY=ρ2L(2L)t=ρt
same as before. Hence, Rx/RY=1
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Comprehension
35 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective
29 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
If each resistance r is along the 12 edges of a cubical skeleton of uniform wires then find the equivalent resistance between X and Y where X and Y are the midpoints of two opposite edges of a face of the cube.
View Solutionxandy are the sides of two squares such that y=x−x2 . Find the rate of the change of the area of the second square with respect to the first square.
View Solution
Knowledge Check
Consider a thin square sheet of side L and thickness t, made of a material of resistivity ρ. The resistance between two opposite faces, shown by the shaded areas in the figure is
 Adirectly proportional to LBdirectly proportional to tCindependent of LDindependent of t.
Adirectly proportional to LBdirectly proportional to tCindependent of LDindependent of t.Consider a thin square sheet of side L and thickness t, made of a material of resistivity ρ. The resistance between two opposite faces, shown by the shaded areas in the figure is
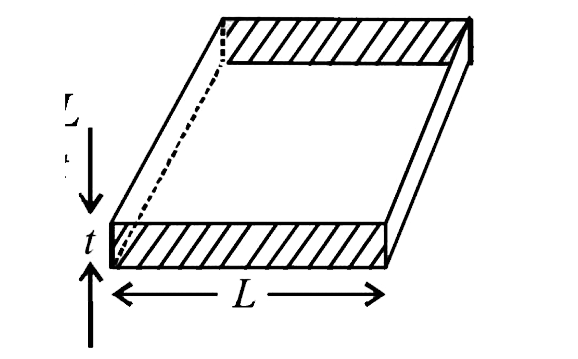 Adirectly proportional to LBdirectly proportional to tCindependent of LDindependent of t
Adirectly proportional to LBdirectly proportional to tCindependent of LDindependent of tx and y are the sides of two square such that y=x−x2. The rate of change of area of the second square with respect to that of the first square is
A2x2+3x+1B2x2+2x−1C2x2−3x+1D3x2+2x+1
If x and y are the sides of two squares such that y=x−x2, find the rate of the change of the area of the second square with respect to the first square.
View SolutionGiven that y=sin3x+43cos3x. What is the maximum rate of change in y with respect to x ?
View SolutionConsider a thin square sheet of side L and thickness t, made of a material of resistivity ρ. The resistance between two opposite faces, shown by the shaded areas in the figure is

View SolutionIf x and y are respectively the areas of a square and a rhombus of sides of same length. Then what is x:y ?
View SolutionIn the carbylamine reaction, R−X converted R−Y via the intermediate Z,R−X,R−YandZ, respectively are
View Solution
