A charge particle A is fixed at the base of a uniform slope of inclination α. Another charge particle B is palced on the slope at an angulare position β measured from the line of greatest slope passing through the position of the first particle. The coefficient of froction between the particle B and the slope is μ(μ<tanα) .For the particle at B to stay in equilibrium what would be the maximum value of the angle β ?

Video Solution
Text Solution
The electrostatic repulsive froce will act along the line joining the two charges along AB. The driving force on particle B are Fe and mg sin α. The friction will act in the direction opposite to the resultant of these forces. Let friction act at an along θ to the line AB.
Let us analyze the force parallel and perpendicular to AB. the forces action on B perpendicular to AB are the cpmponents of friction force fsinθ and (mgsinα)sinβ.
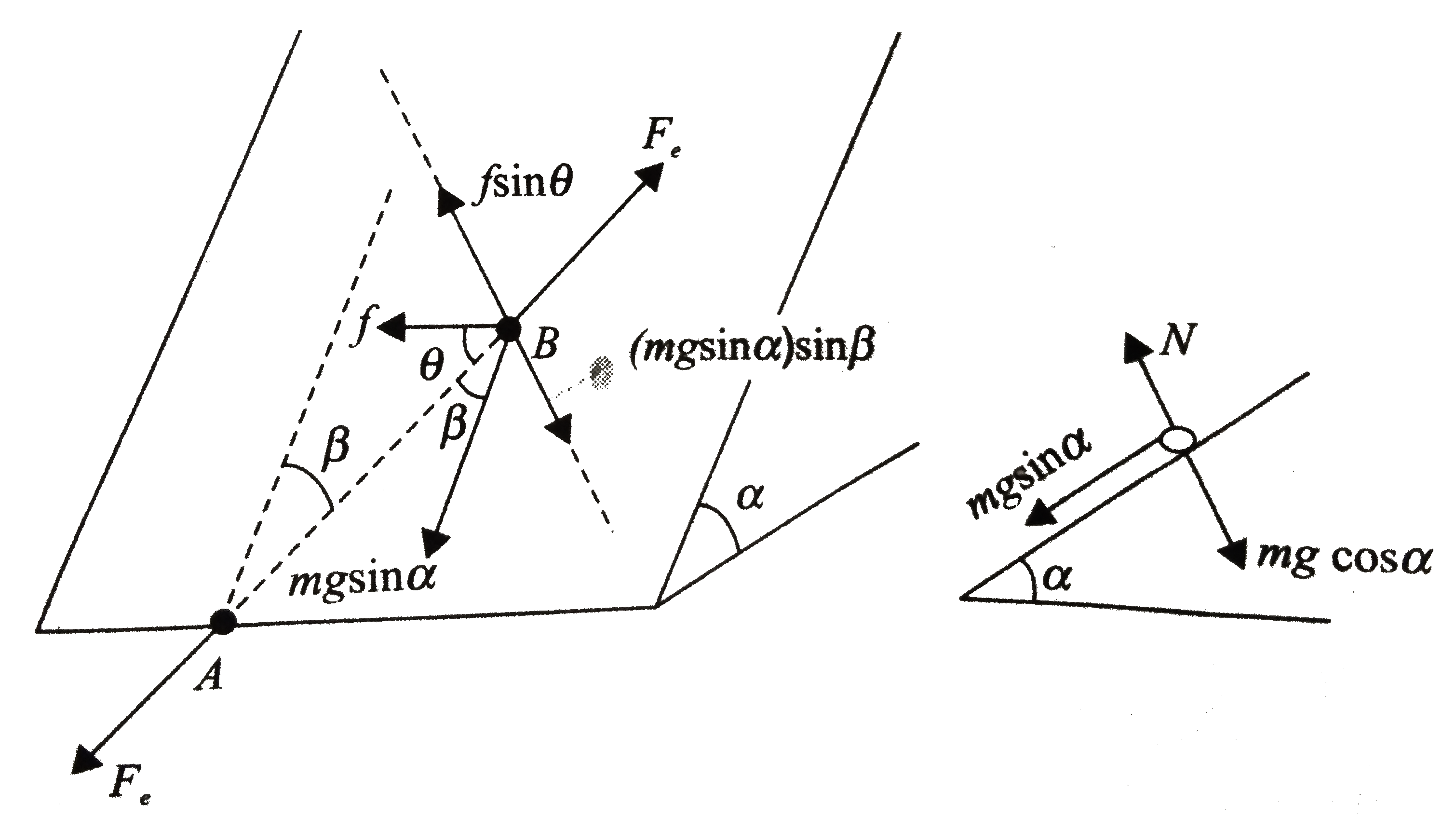
If the particle is in equilibrium
fsinθ=(mgsinα)sinβ
or f=mgsinαsinβsinθ or f≤μmgcosα
or, mgsinαsinβsinθ≤μmgcosα
or sinβ≤μcotα×sinθ
β is maximum when sinθ=1. So
β≤sin−1(μcotα).
|
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Subjective
Explore 32 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Answer Correct Type
Explore 22 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
Knowledge Check
Charge on α−particle is
A4.8×10−19CB1.6×10−19CC3.2×10−19CD6.4×100−19CA particle is projected along the line of greatest slope up a rough plane inclined at an angle of 45∘ with the horizontal. If the coefficient of friction is 1/2 . Their retardation is:
Ag2√2Bg√2Cg√2(1−12)Dg√2(1+12)A heavy particle is projected with a velocity at an angle with the horizontal into the uniform gravitational field. The slope of the trajectory of the particle varies as
A B
B C
C D
D
The charged particle in an atom that contributes positive charge is 'electron'.
View SolutionThe charged particle in an atom that contributes positive charge is 'electron'.
View SolutionThe charged particle in an atom that contributes positive charge is 'electron'.
View SolutionThe charge on α particle is ………The charge on proton
View SolutionThe slope of a line passing through the points A(4, -3) and B(6, -3) is
View Solution

