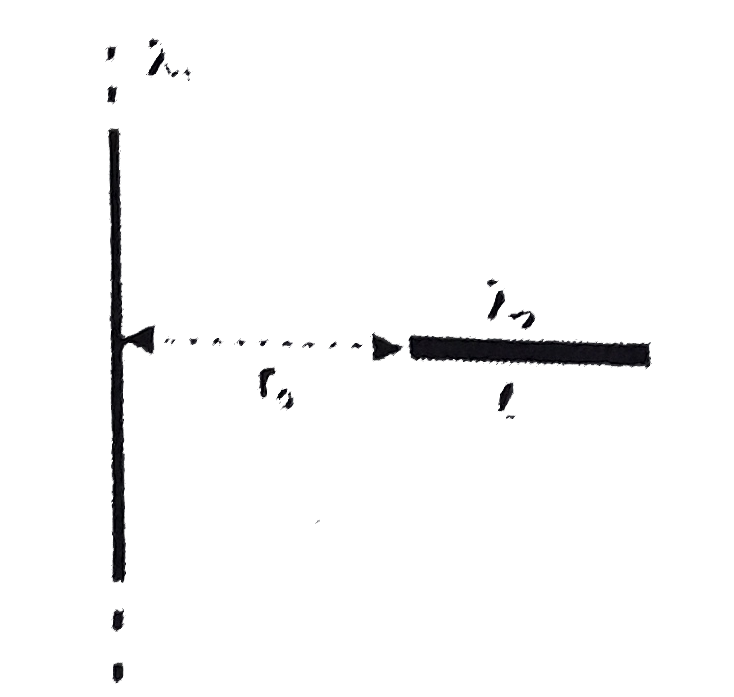
A segment of a charged wire of length l, charge density and an infinitely long chaged wire. Charge density . Lie in a plate at right angles to each other. The sepatation between the wires is . Determine the force of interction between the wires.
To solve the problem of finding the force of interaction between a segment of a charged wire and an infinitely long charged wire, we can follow these steps:
1. Understand the Configuration:
- We have two wires:
- An infinitely long wire with linear charge density λ1.
- A segment of charged wire of length l with linear charge density λ2.
- The wires are oriented at right angles to each other, and the distance between them is r0.
2. Electric Field Due to the Infinite Wire:
- The electric field E at a distance r from an infinitely long charged wire with charge density λ1 is given by:
E=2kλ1r
where k is Coulomb's constant.
3. Consider a Small Element of the Charged Segment:
- Take a small segment dx of the charged wire. The charge dq on this segment is:
dq=λ2dx
4. Calculate the Force on the Small Segment:
- The force dF on the small segment dx due to the electric field E from the infinite wire is:
dF=E⋅dq=(2kλ1r0)⋅(λ2dx)
- Thus, we have:
dF=2kλ1λ2r0dx
5. Integrate to Find the Total Force:
- To find the total force F on the segment of length l, we need to integrate dF from x=0 to x=l:
F=∫l0dF=∫l02kλ1λ2r0dx
- This simplifies to:
F=2kλ1λ2r0⋅l
6. Consider the Effect of Distance:
- However, since the electric field varies with distance, we need to consider the distance x+r0 for each segment:
F=∫r0+lr02kλ1λ2xdx
7. Perform the Integration:
- The integral becomes:
F=2kλ1λ2(ln(x))r0+lr0=2kλ1λ2(ln(r0+l)−ln(r0))
- This simplifies to:
F=2kλ1λ2r0ln(r0+lr0)
8. Final Expression:
- The final expression for the force of interaction between the two wires is:
F=λ1λ22πϵ0ln(1+lr0)
- We have two wires:
- An infinitely long wire with linear charge density λ1.
- A segment of charged wire of length l with linear charge density λ2.
- The wires are oriented at right angles to each other, and the distance between them is r0.
- The electric field E at a distance r from an infinitely long charged wire with charge density λ1 is given by:
E=2kλ1r
where k is Coulomb's constant.
- Take a small segment dx of the charged wire. The charge dq on this segment is:
dq=λ2dx
- The force dF on the small segment dx due to the electric field E from the infinite wire is:
dF=E⋅dq=(2kλ1r0)⋅(λ2dx)
- Thus, we have:
dF=2kλ1λ2r0dx
- To find the total force F on the segment of length l, we need to integrate dF from x=0 to x=l:
F=∫l0dF=∫l02kλ1λ2r0dx
- This simplifies to:
F=2kλ1λ2r0⋅l
- However, since the electric field varies with distance, we need to consider the distance x+r0 for each segment:
F=∫r0+lr02kλ1λ2xdx
- The integral becomes:
F=2kλ1λ2(ln(x))r0+lr0=2kλ1λ2(ln(r0+l)−ln(r0))
- This simplifies to:
F=2kλ1λ2r0ln(r0+lr0)
- The final expression for the force of interaction between the two wires is:
F=λ1λ22πϵ0ln(1+lr0)
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Solved examples
Explore 10 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
An infinitely long string uniformly charged with a linear charge density λ1 and a segment of length l uniformly charge with linear charge density λ2 lie in a plane at right angles to each other and separated by a distance r0 as shown in figure. The force with which these two interact is λ1λ24πε0ln(x). If l=r0, then find the value of x.
View SolutionAn infinitely long string uniformly charged with a linear charge density λ1=1μC/m and a segment of length I uniformly charged with linear charge density λ2=1ln4μ C/M lie in a plane at right angle to each other and separated by a distance lassbown∈thefigure.Determinetheforce (in mN ) with which these two intertct.
'(##CEN_KSR_PHY_JEE_C18_E01_035_Q20##)'
View Solution
Knowledge Check
The electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
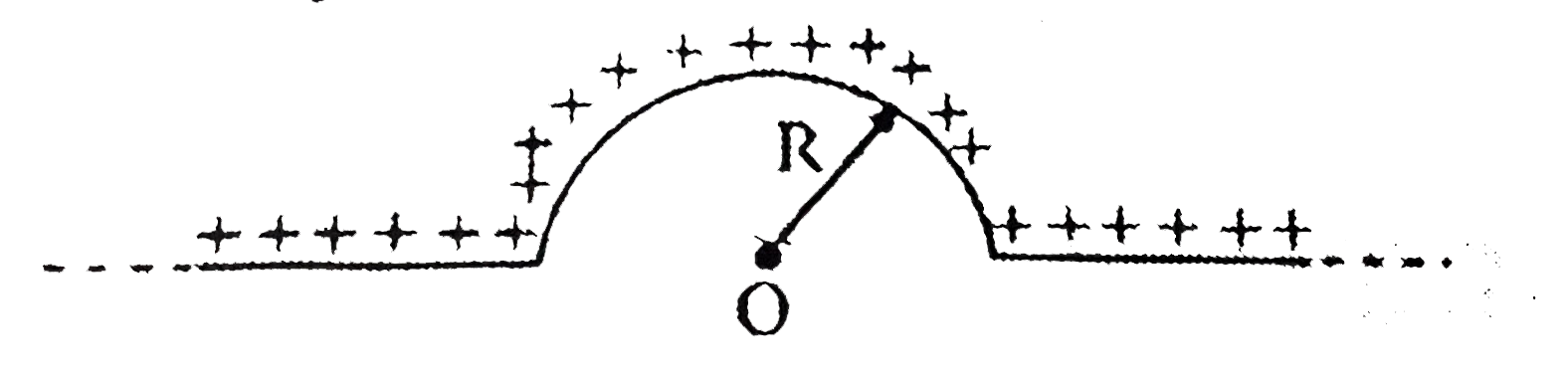 Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
Aλ2πε0RBλ√22πε0RCλ√52πε0RDzeroFind ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
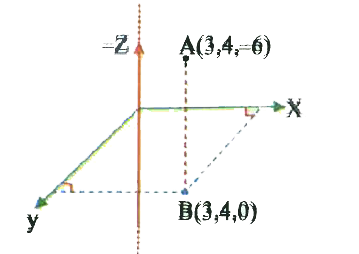 A1:2B1:6C6:1D1:1
A1:2B1:6C6:1D1:1For a long wire of charge density γ,, field at a distance r from the wire is
Aγ2πε0rnBγ4πε0rnC0Dkqεe
Write the expression of electric field due to an infinitely long, straight, wire having linear charge density λ at a point that is at a distance r from it.
View SolutionAn electric dipole of moment p is kept at a distance r form an infinte long charged wire of linear charge density λ as shown.Find the force acting on the dipole?

View SolutionConsider a very long plastic wire with charge density λ .Flux passing through a circle of radius R having centre at one of ends of wire is
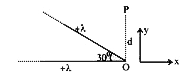
View SolutionAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
View SolutionTwo infinitely long thin styraight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
View Solution