4 bar magnet, held horizontally, is set into angular oscillations in the Earth's magnetic field. It has time periods T1 and T2 at two places, where the angles of dip are θ1 and θ2 respectively. Deduce an expression for the ratio of the resultant magnetic fields at the two places.Solution in Telugu
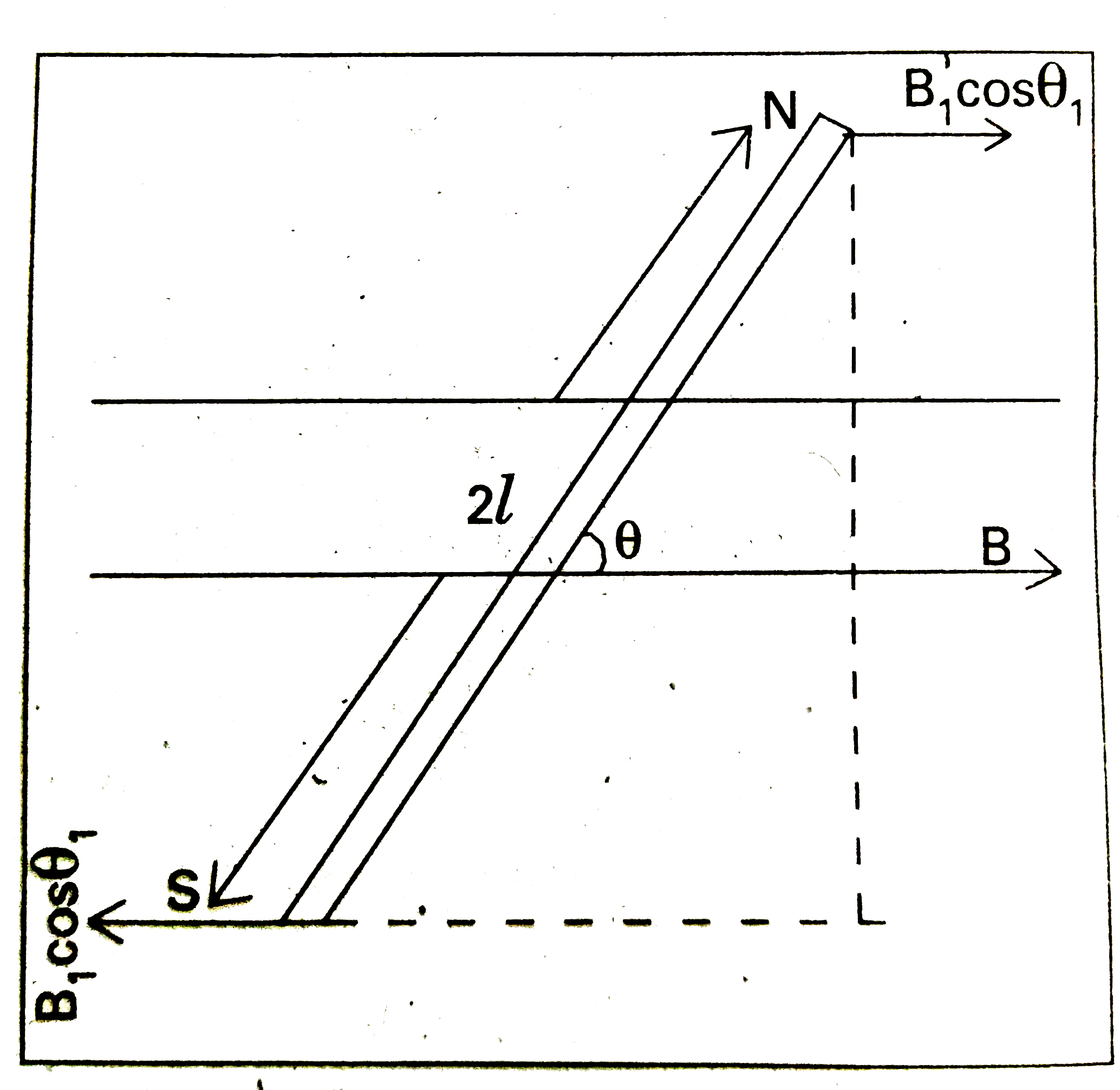
(1) Suppose, the resultant magnetic fields is to be compared at two places A and B.
(2) A barmagnet, field horizontally at A and which is set into angular oscillatins in the Earth's magnetic field.
(3) Let time period of a bar magnet at place 'A' is T1 and angular displacement or angle of dip is θ1.
(4) As the bar magnet is free to rotate horizontally, it does not remain vertical component (B1sinθ1). It can have only horizontal component (B1cosθ1)
(5) The time period of a bar magnet in uniform magnetic field is given by T=2π√ImBH
(6) Now, in this case T=T1 and BH=B1cosθ1
(7) Therefore time period of a bar magnet at place 'A' is given by
T1=2π√ImB1cosθ1 - (1) where I is moment of Inerfia of a barmagnet and m is magnitude of magnetic moment.
(8) Similarly, the same magnet is placed at B and which is set into angular oscillations in the earth's magnetic field.
(9) Let time period of a bar magnet at place B is T2 and angle of dip is θ2.
(10) Since horizontal component of earth's field at B is BH=B2cosθ2, time period, T2=2π√ImB2cosθ2 - (2)
(11) Dividing equation (1) by equation (2), we get T1T2=√mB2cosθ2mB1cosθ1
Squaring on both sides, we have T21T22=B2cosθ2B1cosθ1
(12) But B1=μ0H1 and B2=μ0H2
T12T22=μ0H2cosθ2μ0H1cosθ1
(13) Therefore, H1H2=T22cosθ2T21cosθ1
(14) By knowing T1,T2 and θ1,θ2 at different places A and B, we can find the ratio of resultant magnetic fields.
Topper's Solved these Questions
- MAGNETISM AND MATTERBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:MAGNETISM AND MATTERExercise:Textual Exercises
Explore 27 Videos
- MAGNETISM AND MATTERBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:MAGNETISM AND MATTERExercise:Additional Exercises
Explore 19 Videos
- MAGNETISM AND MATTERBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:MAGNETISM AND MATTERExercise:Short Answer Questions
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:SAQs
Explore 4 Videos
- MOVING CHARGES AND MAGNETISHMBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:MOVING CHARGES AND MAGNETISHMExercise:ADDITIONAL EXERCISES
Explore 26 Videos
Similar Questions
A vector needs three quantities for its specification. Name the three independent quantities conventionally used to specify the earth's magnetic field.
View SolutionWhy does a paramagnetic sample display greater magnetisation (for the same magnetising field) when cooled?
View SolutionDerive an expression for the axial field of a solenoid of radius ''a'', containing ''n'' turns per unit length and carrying current ''I''.
View SolutionWhat is series combination of capacitors. Derive the formula for equivalent capacitance in series combination.
View SolutionTwo concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A, coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.
View SolutionIf the angle of dip at two places are 30^(@) and 45^(@) respectively, then the ratio of horizontal components of earth's magnetic field at the two places will be
View SolutionA magnet oscillating in a horizontal plane has a time period of 2 seconds at a place where the angle of dip is 30^(@) and 3 seconds at another place where the angle of dip is 60^(@) . The retio of resultant magnetic field at the two places is
View SolutionA vibration magnetometer placed in magnetic meridian has a small bar magnet. The magnet executes oscillations with a time period of 2 sec in earth's horizontal magnetic field of 24 microtesla. When a horizontal field of 18 microtesla is produced opposite to the earth's field by placing a current carrying wire, the new time period of magnet will be
View SolutionA bar magnet, held horizontally, is set intom angular oscillations in earth's magnetic field. It has time periods T_(1) and T_(2) at two place, where the angles of dip are delta_(1) and delta_(2) respectively. Deduce an expression for the ratio of the resultant magnetic fields at the two places.
View SolutionA magnet oscillating in a horizontal plane, has a time period of 3 seconds at a place where the angle of dip is 30^(@) and 4 seconds at another place, where the dip is 60^(@) . Compare the resultant magnetic field at the two places.
View SolutionA bar magnet is pivoted at its centre and placed in such a manner that it can freely rotate in horizontal plane. Time period of oscillation for this magnet in earth's magnetic field is measured at two different places. Time period of oscillation is 3s at a place where angle of dip is 30^@ and time period is 4s at a place where angle of dip is 60^@ . Let B_1 and B_2 are the net magnetic fields due to earth at two places in same order. Then B_1//B_2
View SolutionA bar magnet , held horizontally , is set into angular oscillations in the earth's magnetic field its time periods are T_(1) and T_2 at two places where the angles of dip are theta_(1) and theta_2 , respectively . The ratio of the resultant magnetic fields at these two places will be
View SolutionThe magnetic dip angle at two places are 30° and 45°. Calculate ratio of horizontal components of earth's magnetic field at the two places. Magnetic field at the places is equal to .......
View SolutionAt two different places the angles of dip are respectively 30∘ and 45∘. At these two places the ratio of horizontal component of earth's magnetic field is
View Solutionक्षैतिज तल में लटकी हुई दो छड़ चुम्बक पृथ्वी के चुम्बकीय क्षेत्र में दोलन काल T1 तथा T2 से दोलन कर रही है इनके चुम्बकीय द्विध्रुव आघुर्णो का अनुपात होगा :
View Solution

