A disc having radius R is rolling without slipping on a horizontal (x−z) plane. Centre of the disc has a velocity v and acceleration a as shown. 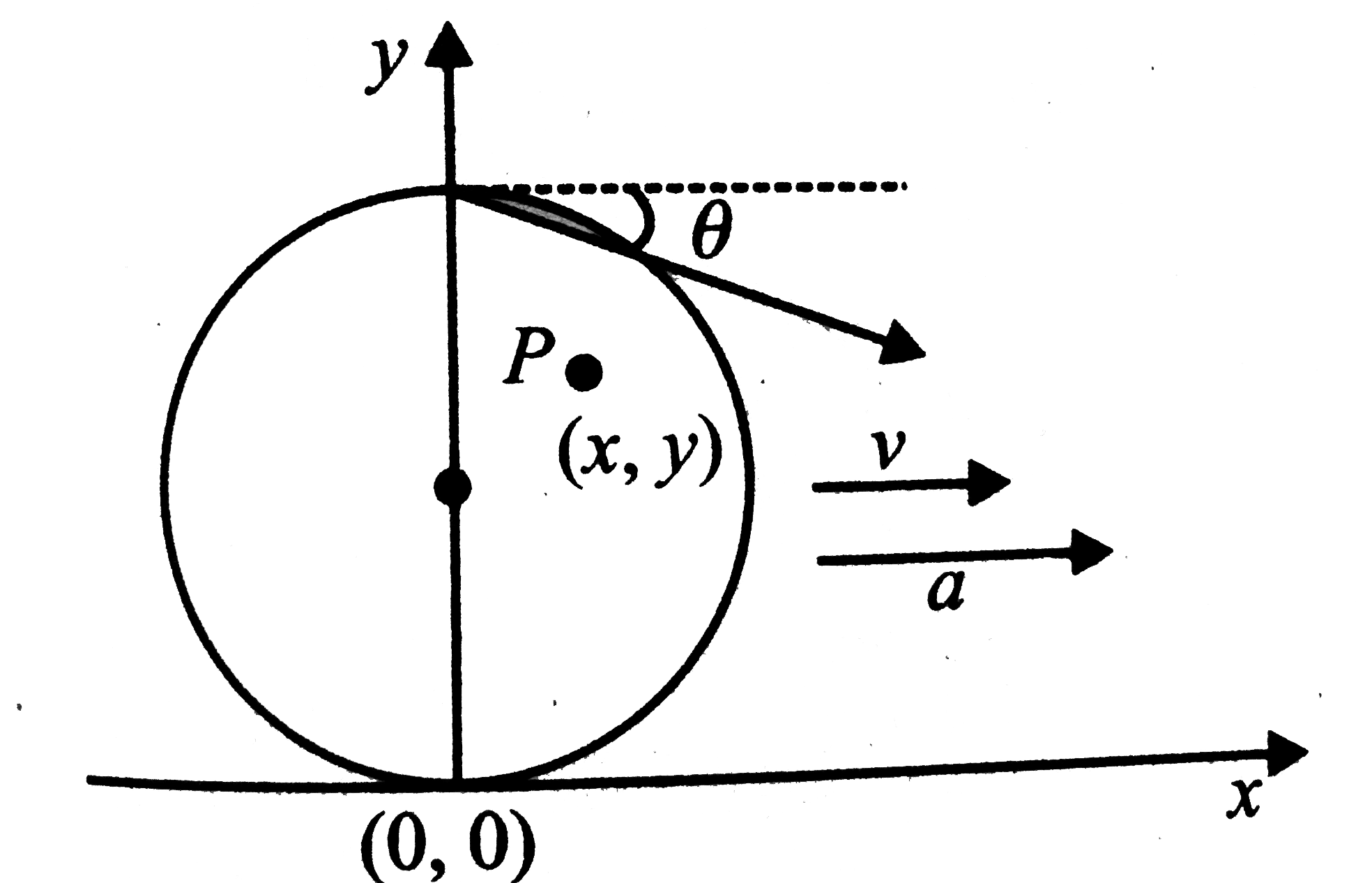
If v=√2aR the angle ρ between acceleration of the top most point and the horizontal is
0
45∘
tan−1(2)
tan−1(12)
The correct Answer is:B
a=αR

aC=ω2R−(vR)2R=v2R=2aRR=2a
tanθ=2a2a=1⇒θ=45∘
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:MCQ_TYPE
Explore 20 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
Similar Questions
A circular disc of radius r is rolling without slipping on a horizontal surface. What is the ratio of the translational KE and rotational KE of disc ?
View SolutionA uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : the centre of mass
View Solution
Knowledge Check
A disc having radius R is rolling without slipping on a horizontal (x−z) plane. Centre of the disc has a velocity v and acceleration a as shown.

Speed of point P having coordinates (x,y) isAv√x2+y2RBv√x2+(y+R)2RCv√x2−(y−R)2RDnone
A wheel is rolling without slipping on a horizontal plane with velocity v and acceleration a of centre of mass as shown in figure. Acceleration atAA is vertically upwardsBB may be vertically downwardsCC cannot be horizontalDA point on the rim may be horizontal leftwards.A wheel is rolling on a horizontal plane. At a certain instant it has a velocity v and acceleration a of CM as shown in figure . Acceleration of
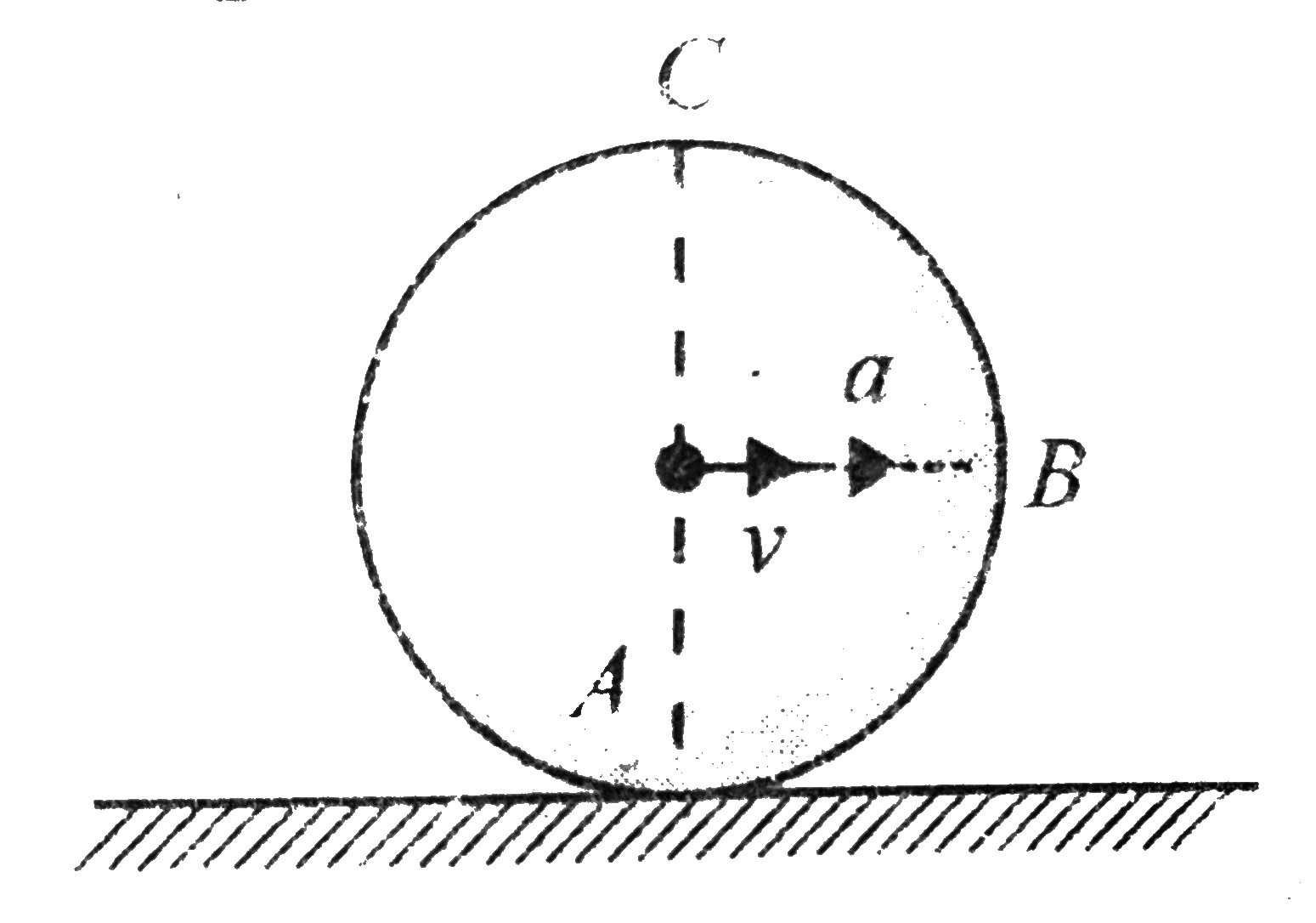 AA is vertically upwardsBB may be vertically down-wardsCC cannot be horizontalDsome point on the rim may he horizontal leftwards
AA is vertically upwardsBB may be vertically down-wardsCC cannot be horizontalDsome point on the rim may he horizontal leftwards
A circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View SolutionThe disc of radius r is confined to roll without slipping at A and B. If the plates have the velocities shown, then
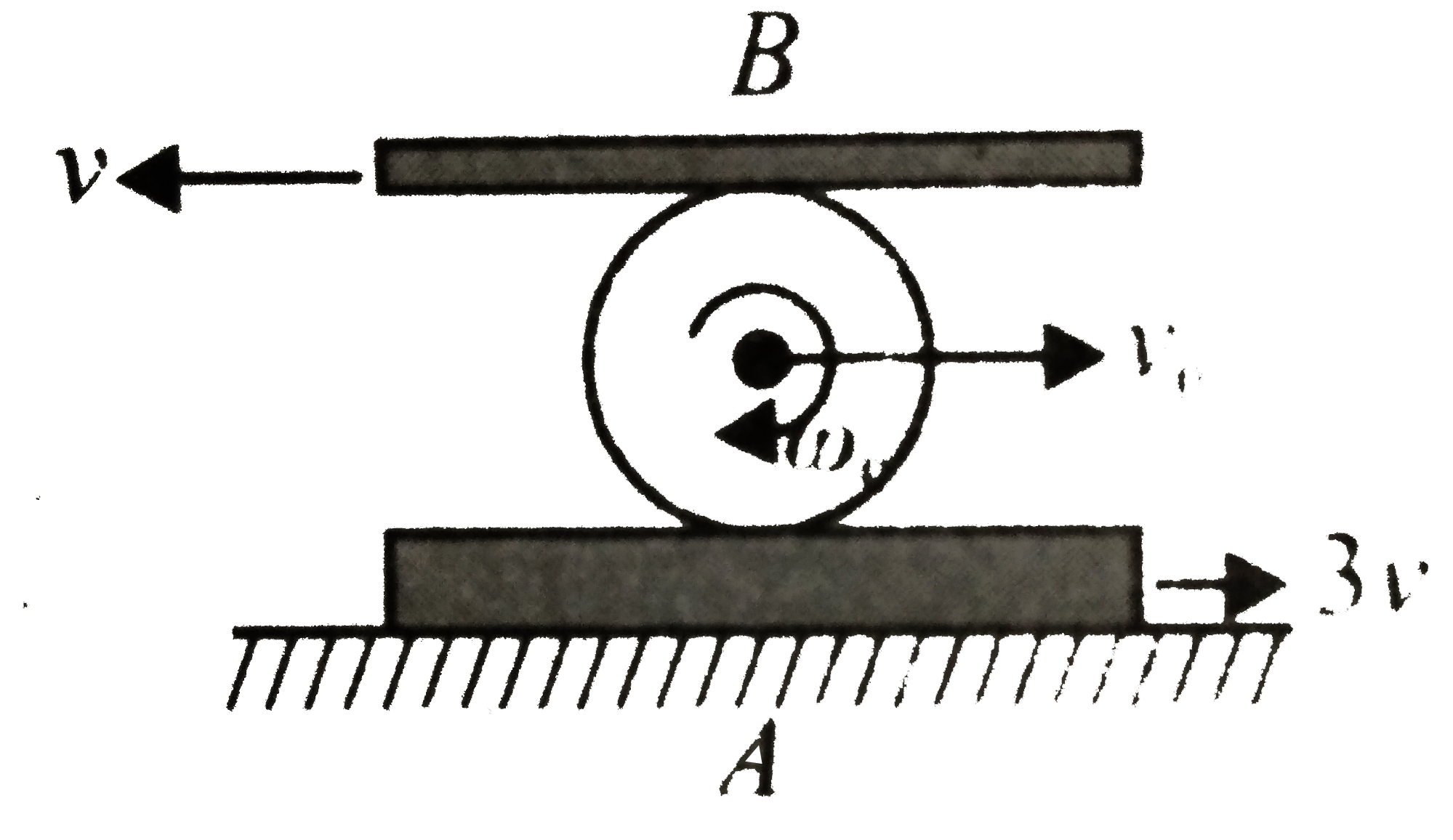
View SolutionA disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is

View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P is
View Solution

