Question

The minimum and maximum distances of a satellite from the center of the earth are $2R$ and $4R$ respectively, where $R$ is the radius of earth and $M$ is the mass of the earth . Find
(a) its minimum and maximum speeds,
(b) radius of curvature at the point of minimum distance.

Options

A. `sqrt((GM)/(9R)), sqrt((2GM)/(R))`
B. `sqrt((GM)/(5R)), sqrt((3GM)/(2R))`
C. `sqrt((GM)/(6R)), sqrt((2GM)/(3R))`
D. `sqrt((GM)/(3R)), sqrt((5GM)/(2R))`

Answer

C

Explanation

Applying the principle of conservation of angular momentum,
`mv_(1)(2R)=mv_(2)(4R)`
`v_(1)=2v_(2)`……i
From conservation of energy
`1/2mv_(1)^(2)-(GMm)/(2R)=1/2mv_(2)^(2)-(GMm)/(4R)`……….ii
Solving eqn i and ii we get
`v_(2)=sqrt((GM)/(6R)), v_(1)=sqrt((2GM)/(3R))`
If `r` is the radius of curvature at point `A`.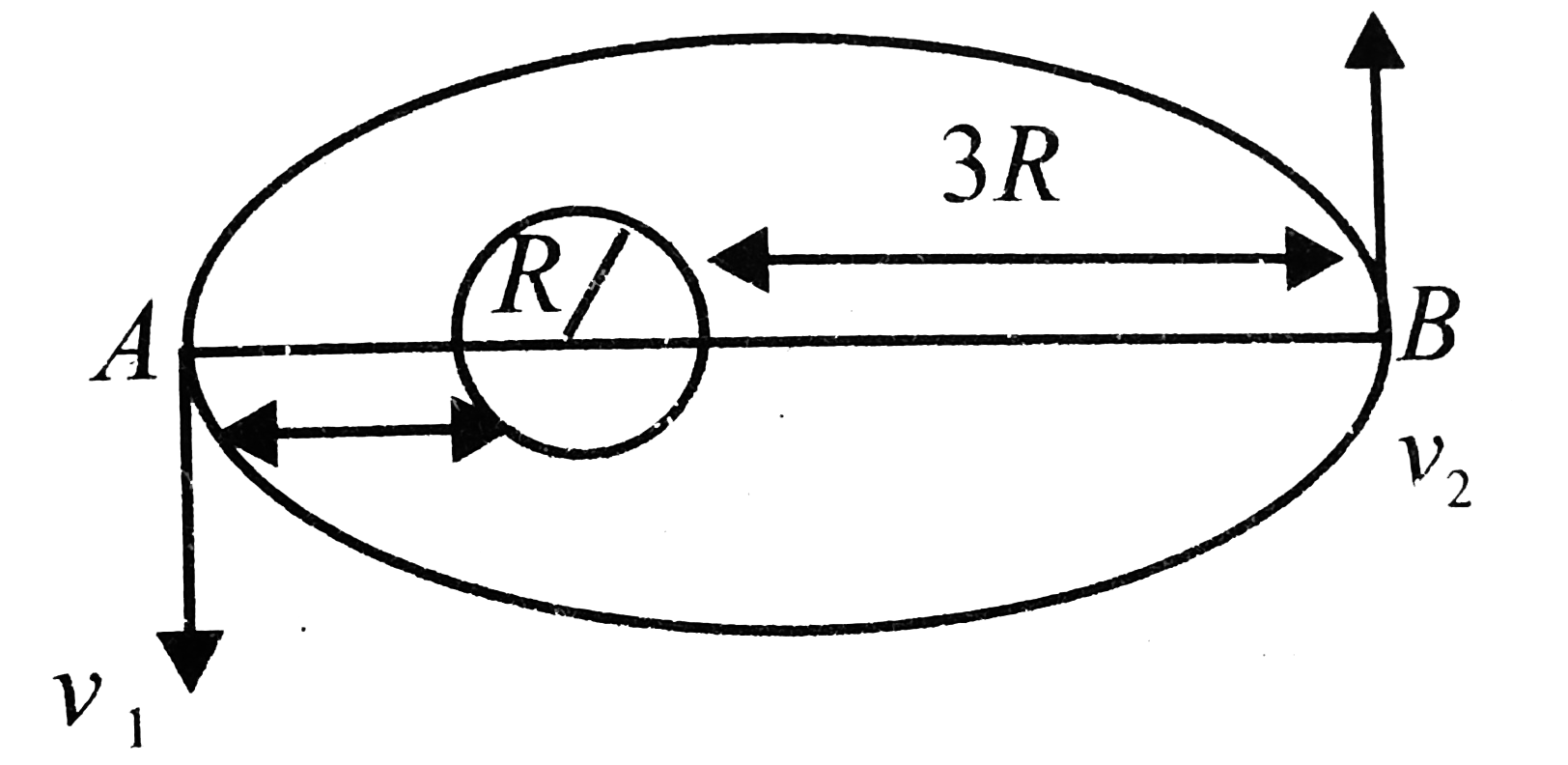
`(mv_(1)^(2))/r=(GMm)/((2R)^(2))`
`r=(4v_(1)^(2))/(GM)=(8R)/3` (putting value of `v_(1)`)