A satellite is orbiting around the earth in a circular orbit of radius . A particle of mass is projected from the satellite in a forward direction with a velocity times the orbital velocity (this velocity is given w.r.t. earth). During subsequent motion of the particle, its minimum distance from the centre of earth is
The correct Answer is:A
As the velocity of the particle is les than the orbital velocity of the satellite, the particle goes in the elliptical orbit of the semi major axis less than r.
Let be the minimum distance and be the velocity of the particle at this position, then
where is the mass of the particle and is the orbital speed equal to . 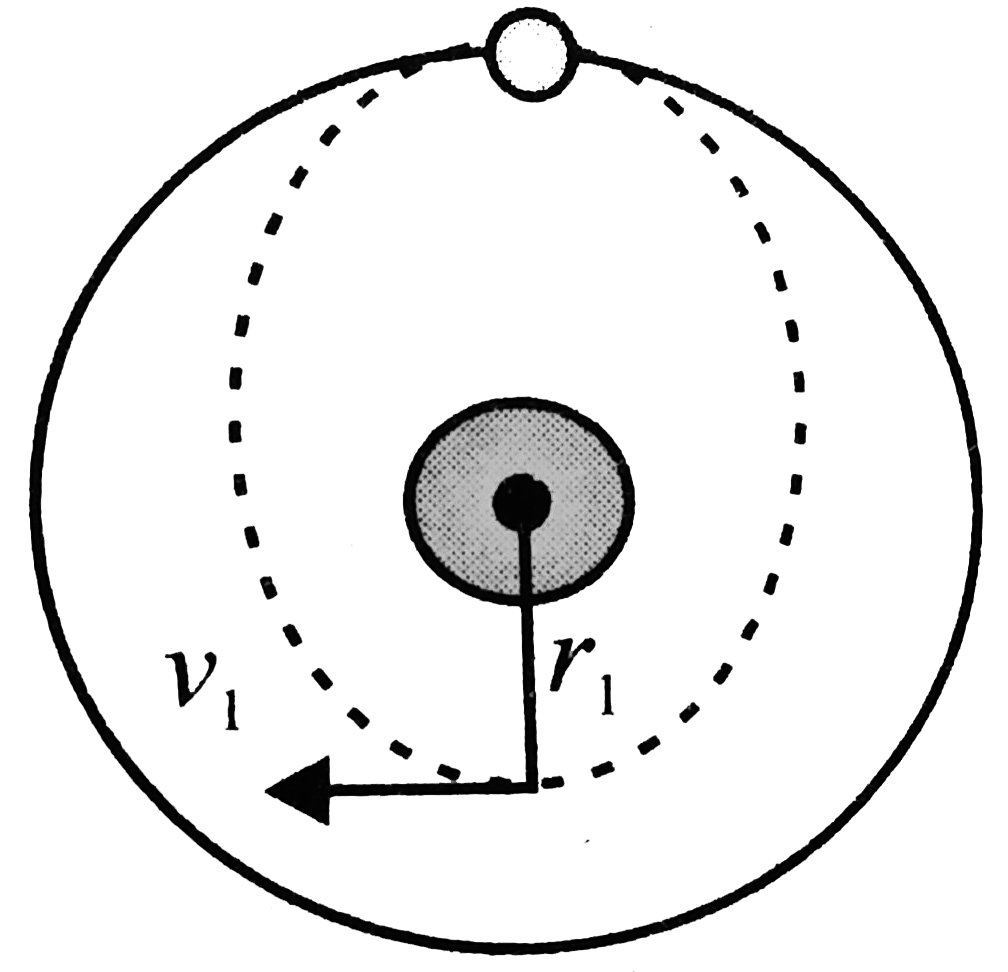
From energy conservation
Solving the equations we get
Topper's Solved these Questions
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Multiple Correct
Explore 24 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Assertion- Reasoning
Explore 13 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Subjective
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
Similar Questions
A satellite is revolving round the earth (mass Me) in a circular orbit of radius a with velocity V0 A particle of mass m is projected from the satellite in forward direction with relative velocity v[√54−1]V0. During subsequent motion of particle.
View SolutionA satellite has to revolve round the earth in a circular orbit of radius 8×103 km. The velocity of projection of the satellite in this orbit will be -
View Solution
Knowledge Check
A satellite is orbiting around earth in a circular orbit of radius r. A particle of mass m is projected from satellite in forward direction with velocity v=√23 times orbital velocity (this velocity is with respect to the earth). During subsequent motion of the particle, its minimum distance from the centre of earth is
Ar2BrC2r3D4r3A satellite is orbiting the earth in a circular orbit of radius r. Its
Akinetic energy veries as rBangular momentum varies as r−1Clinear momentum varies as r2Dfrequency of revolution varies as r−3/2When a satellite going around the earth in a circular orbit of radius r and speed v loses some of its energy, then
Ar and v both increasesBr and v both decreasesCr will increases and v will decreasesDr will decreases and v will increases
A satellite is revolving round the earth in a circular orbit of radius r and velocity υ0. A particle is projected from the satellite in forward direction with realative velocity υ=(√5/4−1)υ0. Calculate its minimum and maximum distances from earth's centre during subsequent motion of the particle.
View SolutionA satellite is orbiting around earth with its orbit radius 16 times as great as that of parking satellite. What is the period of this satellite.
View SolutionThe satellite of mass m is orbiting around the earth in a circular orbit with a velocity v.What will be its total energy ?
View SolutionA satellite is revolving in circular orbit of radius r around the earth of mass M. Time of revolution of satellite is
View SolutionSatellites A and B are orbiting around the earth in orbits of ratio R and 4R respectively. The ratio of their areal velocities is-
View Solution

