Consider two satellites A and B of equal mass, moving in the same circular orbit of radius r around the earth but in the opposite sense and therefore a collision occurs.
(a) Find the total mechanical energy EA+EB of the two satellite-plus-earth system before collision.
(b) If the collision is completely inelastic, find the total mechanical energy immediately after collision. Describe the subsequent motion of the combined satellite.
−2GMmr
−GMmr
GMm2r
GMm4r
The correct Answer is:A
Energy of each satellite in the orbit=−GMm2r
Total energy of the system before collision
Ei=E1=E=2E=−2×Gmm2r=−GMm2r
As the satellites of equal mass are moving in the opposite directions and collide inelasticaly, the velocity of the wreckage just after the collision is
mv−mv=2mV, i.e. V=0
The energy of the wreckege comes to standstill in the orbit, it will move along the radius towards the earth under gravity.
Topper's Solved these Questions
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Multiple Correct
Explore 24 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Assertion- Reasoning
Explore 13 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Subjective
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
Similar Questions
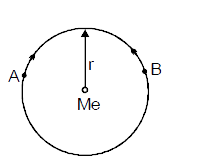
Consider two satellites A and B of equal mass m, moving in the same circular orbit of radius r around the earth E but in opposite sense of rotation and therefore on a collision course (see figure).
In terms of G, Me, m and r find the total mechanical energy EA + EB of the two satellite plus earth system before collision.
View Solution_E01_109_Q01.png)
Consider two satellites A and B of equal mass m, moving in the same circular orbit of radius r around the earth E but in opposite sense of rotation and therefore on a collision course (see figure)
(i). In terms of G,Me m and r find the total mechanical energy EA+EB of the two satellite plus earth system before collision
(ii). If the collision is completely inelastic so that wreckage remains as one piece of tangled material (mass=2m) find the total mechanical energy immediately after collision.
(iii). Describe the subsequent motion of the wreckage.
View Solution
Knowledge Check
The collision between both blocks shown in figure is completely inelastic. The total energy of oscillation after collision is
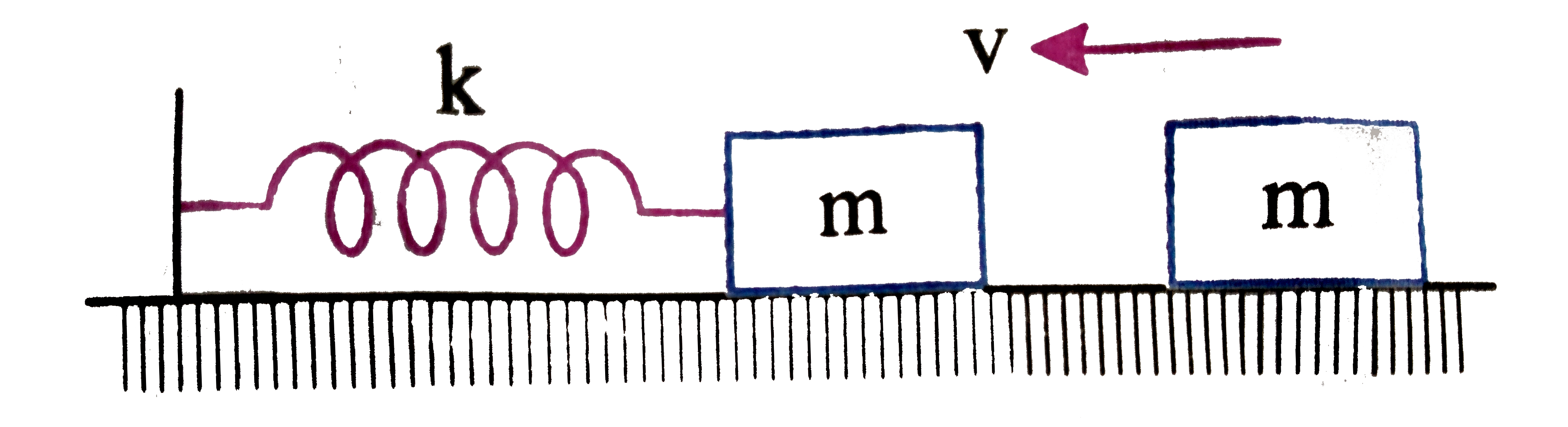 A12mv2Bmv28Cmv24Dmv232
A12mv2Bmv28Cmv24Dmv232The satellite of mass m revolving in a circular orbit of radius r around the earth has kinetic energy E. then, its angular momentum will be
A√Emr2BE2mr2Csqt(2Emr2)D√2EmrA satellite of mass M revolving in a circular orbit of radius rs around the earth of mass M has a total energy E. then, its angular momentum will be
A√Emsr2sBE2msr2sC(2Emsr2s)1/2D√2Emsrs
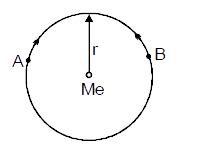
Consider two satellites A and B of equal mass m, moving in the same circular orbit of radius r around the earth E but in opposite sense of rotation and therefore on a collision course (see figure).
If the collision is completely inelastic so that wreckage remains as one piece of tangle d material (mass = 2m), find the total mechanical energy immediately after collision.
View SolutionTwo satellite of same mass are launched in the same orbit of radius r around the earth so as to rotate opposite to each other. If they collide inelastically and stick together as wreckage, the total energy of the system just after collision is
View SolutionConsider two satellites A and B of equal mass m, moving in the same circular orbit about the earth, but in opposite sense as shown in figure. The orbital radius is R. The satellite undergo a collision which is perfectly inelastic. For this situation, mark out the correct statements. [Take mass of earth as M]
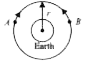
View SolutionConsider two satellites A and B of equal mass m, moving in the same circular orbit about the earth, but in the opposite sense as shown in Fig. The orbital radius is r. The satellites undergo a collision which is perfectly inelastic. For this situation, mark out the correct statement(s). [Take mass of earth as M]

View SolutionTwo satellite A and B , ratio of masses 3:1 are in circular orbits of radii r and 4 r . Then ratio of total mechanical energy of A to B is
View Solution

