The planets with radii R1 and R2 have densities p1,p2 respectively. Their atmospheric pressues are p1 and p2 respectively.Therefore, the ratio of masses of their atmospheres, neglecting variation of g within the limits of atmoshpere is
p1R2ρ1p2R1ρ2
p1R2ρ2p2R1ρ1
p1R1ρ1p2R2ρ2
p1R1ρ2p2R2ρ1
The correct Answer is:D
p=ρatmgh=m43π[(R+h)3−R]GMR2h
⇒p=m43πR3[(1+hR)3−1)×G43πR3l0R2×h
m43πR3[(1+3hh−1]×G43πRl0h (Here M=43πR3l0)
Here p=mGρ3R
=∴M∝pRρ
Topper's Solved these Questions
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Multiple Correct
Explore 24 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Assertion- Reasoning
Explore 13 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Subjective
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
Similar Questions
Knowledge Check
The planets with radii R1 and R2 have densities p1,p2 respectively. Their atmospheric pressues are p1 and p2 respectively.Therefore, the ratio of masses of their atmospheres, neglecting variation of g within the limits of atmoshpere is
Ap1R2ρ1p2R1ρ2Bp1R2ρ2p2R1ρ1Cp1R1ρ1p2R2ρ2Dp1R1ρ2p2R2ρ1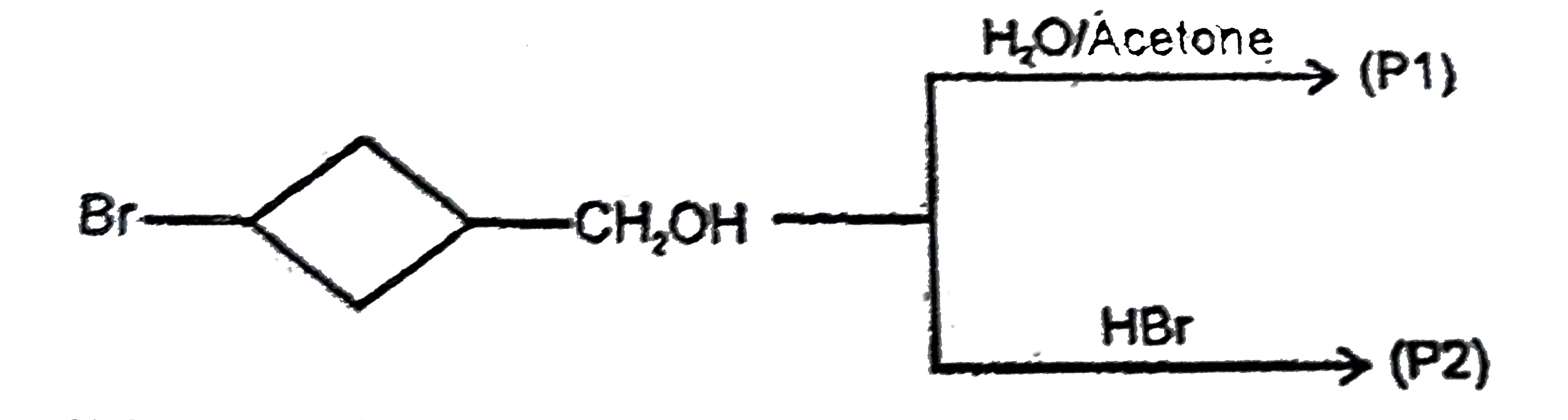
P1 and P2 are respectively :A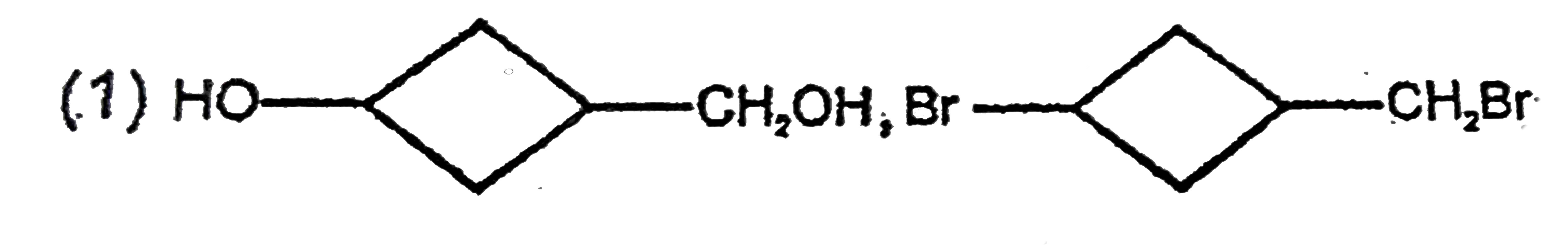 B
B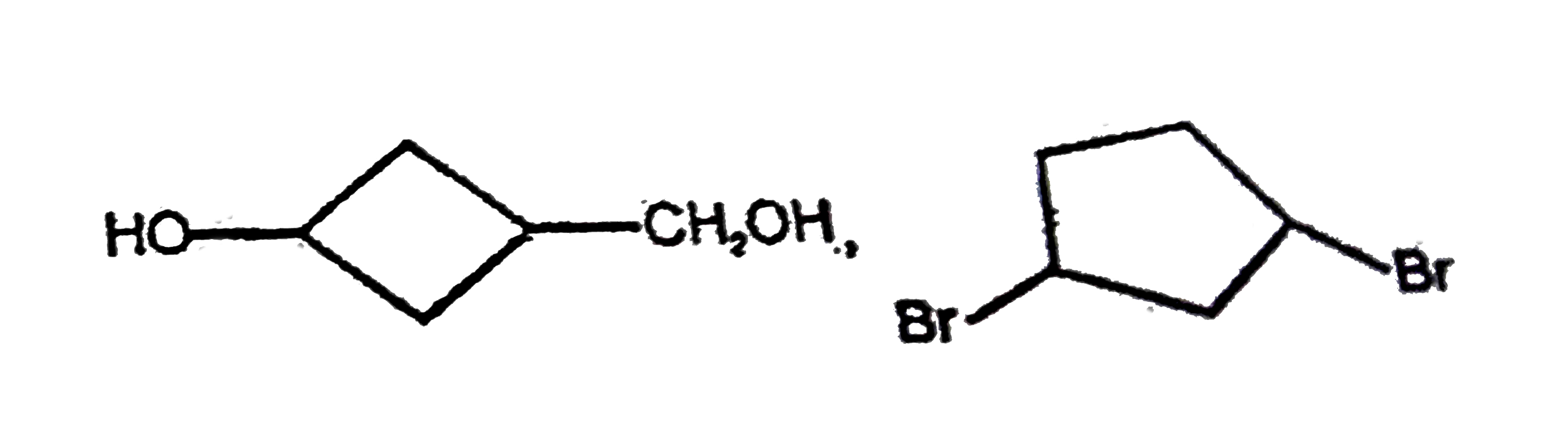 C
C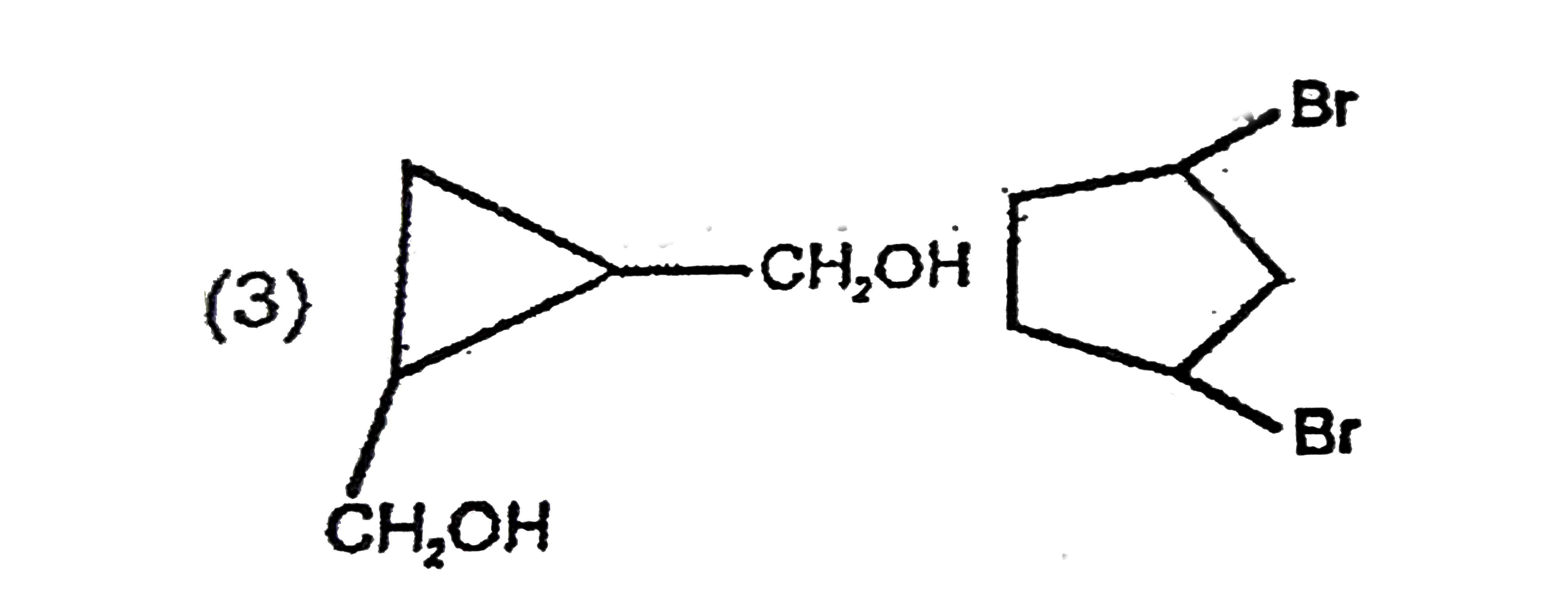 D
D
Two planets have radii r1andr2 and densities d1andd2 respectively. Then the ratio of acceleration due to gravity on them is
Ar1d1:r2d2Br1d2:r2d1Cr21d1:r22d2Dr22d1:r21d2
If two planets of radii R1andR2 have densities d1andd2, then the ratio of their respective acceleration due to gravity is
View SolutionN2O4 is dissociated to 33% and 40% at total pressure P1andP2 atm respectively. Then the ratio P1/P2 is
View SolutionTwo planets have the same average density but their radii are R1 and R2. If acceleration due to gravity on these planets be g1 and g2 respectively, then
View SolutionThe radii of two planets are respectively R1andR2 and their densities are respectively ρ1andρ2.The ratio of the accelerations due to gravity at their surface is
View SolutionIf two liquids of same masses but densities p1 and p2, respectively are mixed, then the density of mixture is given by
View Solution

