A rock is found to weigh w in air when suspended from a spring scale. When completely submerged in water while attached to the spring scale, it weighs wsubmerged as shown in Fig. Find the density of the rock ρrock in terms of Rock the scale reading and the density of water

Let the volume of the rock be V, then magnitude of its weight.
w=ρirockVg
In water, rock experiences an additional buoyant force with a magnitude equal to that the weight of the water displaced by the system. Buoyant force has magnitude

Fbuoy=ρwaterVg
The new scale reading is the total downward force on the system when it is the water
wsubmerge=w−Fbuoy−ρrockVg−ρwaterVg
From the ratio wsubmergew=ρrockVg−ρwaterVgρrockVg
=ρrock−ρwaterρrock
solving for the density of the system (i.e the rock )
ρrock=ww−wsubmergeρwater
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.2
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
The reading of a spring balance when a block is suspended from it iin air is 60 N the reading is changed to 40 N when the block is submerged in water. Find the relative density of the block.
View SolutionA beaker of mass 1 kg contains 2 kg of water and rests on a scale. A 2kg block of aluminum (specific gravity 2.70) suspended from a spring scale is suspended from a spring scale is submerged in water, as shown in figure. Find the readings of both scales.
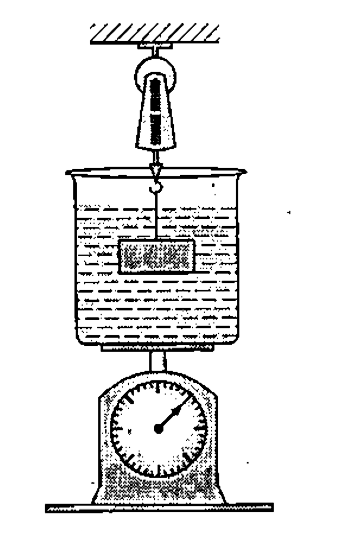
View Solution
Knowledge Check
The reading of a spring balance when a block is suspended from it in air is 60 N. This reading is changed to 40 N when the block is submerged in water. The relative density of the block is:
A3B2C6D32A spring balance shows 100 gf reading when a metallic sphere is suspended from its hook. When the completely immersed in water, the reading shown by the balance is 75gf. The relative density of the material of the sphere is
A1B2C3D4A wire is suspended vertically from a rigid support. When loaded with a steel weight in air, the wire extends by 16cm. When the weight is completely immersed in Water, the extension is reduced to 14cm. The relative density of the material of the weight is
A2g/cm3B6g/cm3C8g/cm3D16g/cm3
A certain block weighs 15 N in air. But is weighs only 12 N when completely immersed in water. When immersed completely in another liquid, it weighs 13 N. Calculate the relative density of (i) the block and (ii) the liquid.
View SolutionA block hangs from a spring balance. The balance reads 40 N in air, 35 N when block is immersed in water and 25 N when block is immersed in another liquid. Find the density of block and other liquid.
View SolutionA metal ball weighs 0.096N.When suspended in water it has an apparent weight of 0.071N. Find the density of the metal.
View SolutionA stell wire is suspended vertically from a rigid support. When loaded with weight in air, it extends by x1. When the weight is completely inside the water, the extension becomes x2. Find the relative density of the meterial fo the weight ?
View SolutionA body is suspended on a spring balance in a ship sailing along the equator with a speed v'. If ω is the angular speed of the earth and ω0 is the scale reading when the ship is at rest, the scale reading when the ship is sailing is
View Solution
