Two lock gates of $7.5 m$ height are provided in a canal of $16 m$ width meeting at an angle of $120^{\circ}$ . Calculate the force acting on each gate when the depth of water in upstream side is $5 m$ .

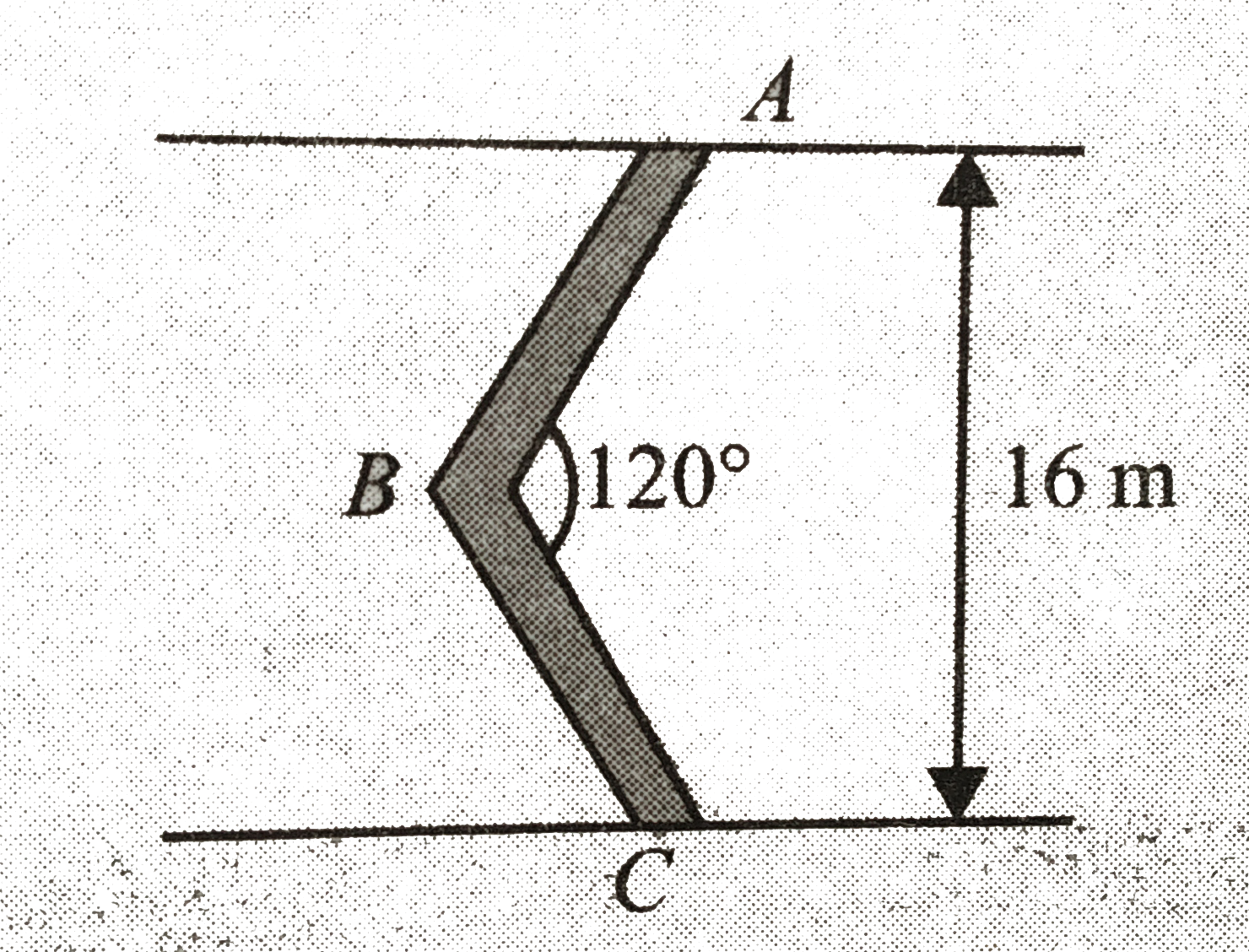
$1133 k N$

$1200 k N$

$578 k N$

$1566 k N$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

A water tank has the shape of an inverted right circular cone, whose semi-vertical angle is ${tan}^{- 1} (\frac{1}{2})$ . Water is poured into it at a constant rate of 5 cu m/min. Then, the rate (in m/min) at which the level of water is rising at the instant when the depth of water in the tank is 10 m is
A $\frac{2}{π}$
B $\frac{1}{5 π}$
C $\frac{1}{15 π}$
D $\frac{1}{10 π}$
Two forces each of magnitude $10 N$ act simultaneously on a body with their directions inclined to each other at an angle of $120^{\circ}$ and displaces the body over $10 m$ along the bisector of the angle between the two forces. Then the work done by force is
A5 J
B1 J
C50 J
D100 J
There are two charges +1 $μ C$ and $+ 5 μ C$ , separated by a distance of 0.2 m in air, the ratio of forces acting in them will be:
A $1 : 5$
B $5 : 1$
C $1 : 1$
D $1 : 25$