A liquid of density ρ is filled in a beaker of cross section S to a height H and then a cylinder of mass m and corss section s is made to float in it as shown in figure. It the atmospheric pressure is p0, find the pressure a at the top face A of the cylinder b at the botom face C of the cylinder and c. at the base B of the beaker. Can ever these three pressures be equal?

a. Above the cros section A, there is external presue due to atmosphere only. So pA= atmospheric pressure =p0
b. At point C the pressure will be due to atmosphere and also due to the weight of the cylinder ie.
pC=p0=mgs
c. If the system is in a state of free fall (as in a satellite) i.e, g→0, then pA=pC=PB=P0 [as weight =0]
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Solved Examples
Explore 7 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.1
Explore 11 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A liquid of density ρ is filled in a beaker of cross section A to a height H and then a cylinder of mass M and cross-section a is made to float in it as shown in

If the atmospheric pressure is P0 find the pressure (a) at the top face B of the cylinder (b) at the bottom face C of the cylinder and (c ) at the base D of the beaker. (d) Can ever these pressure be equal ?
View SolutionA cylinderical vessel contaning liquid is closed by a smooth piston of mass m. the area of cross-section of the piston is A. if the atmospheric pressure is P0, Find the pressure of the liquid just below the piston.
View Solution
Knowledge Check
A cylinder is floating in two liquids as shown in figure. Choose the correct options.
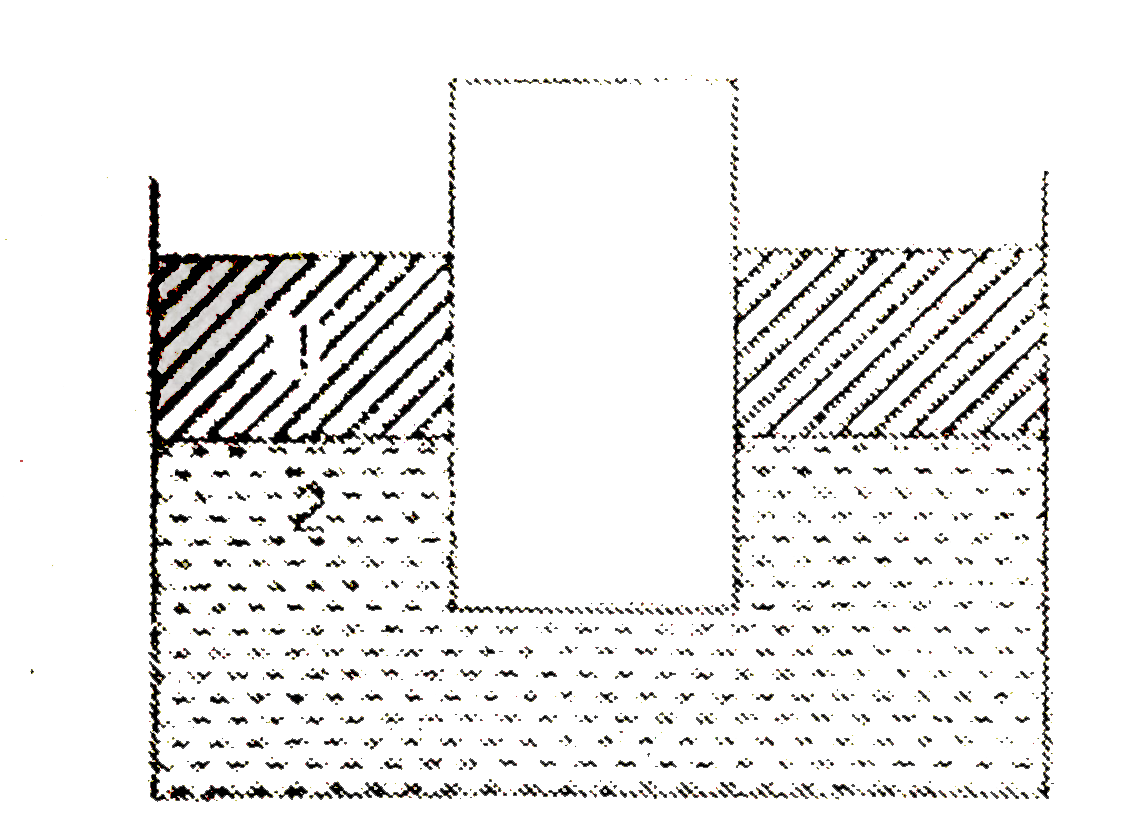 ANet force on cylinder by liquid 1 is zeroBNet force on cylinder by liquid 1 is non-zeroCNet force on cylinder by liquid 2 is equal to the upthrustDNet force on cylinder by liquid 2 is more then the upthrust
ANet force on cylinder by liquid 1 is zeroBNet force on cylinder by liquid 1 is non-zeroCNet force on cylinder by liquid 2 is equal to the upthrustDNet force on cylinder by liquid 2 is more then the upthrustA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
AhBaCρDgA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)
 AρghBρalCρ(gh+al)DBoth (a) and (b)
AρghBρalCρ(gh+al)DBoth (a) and (b)
A cylinder contains He at 2 atmosphere pressure and hydrogen at 1.5 atmosphere pressure. What is the pressure of the mixture of gases in the cylinder ?
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
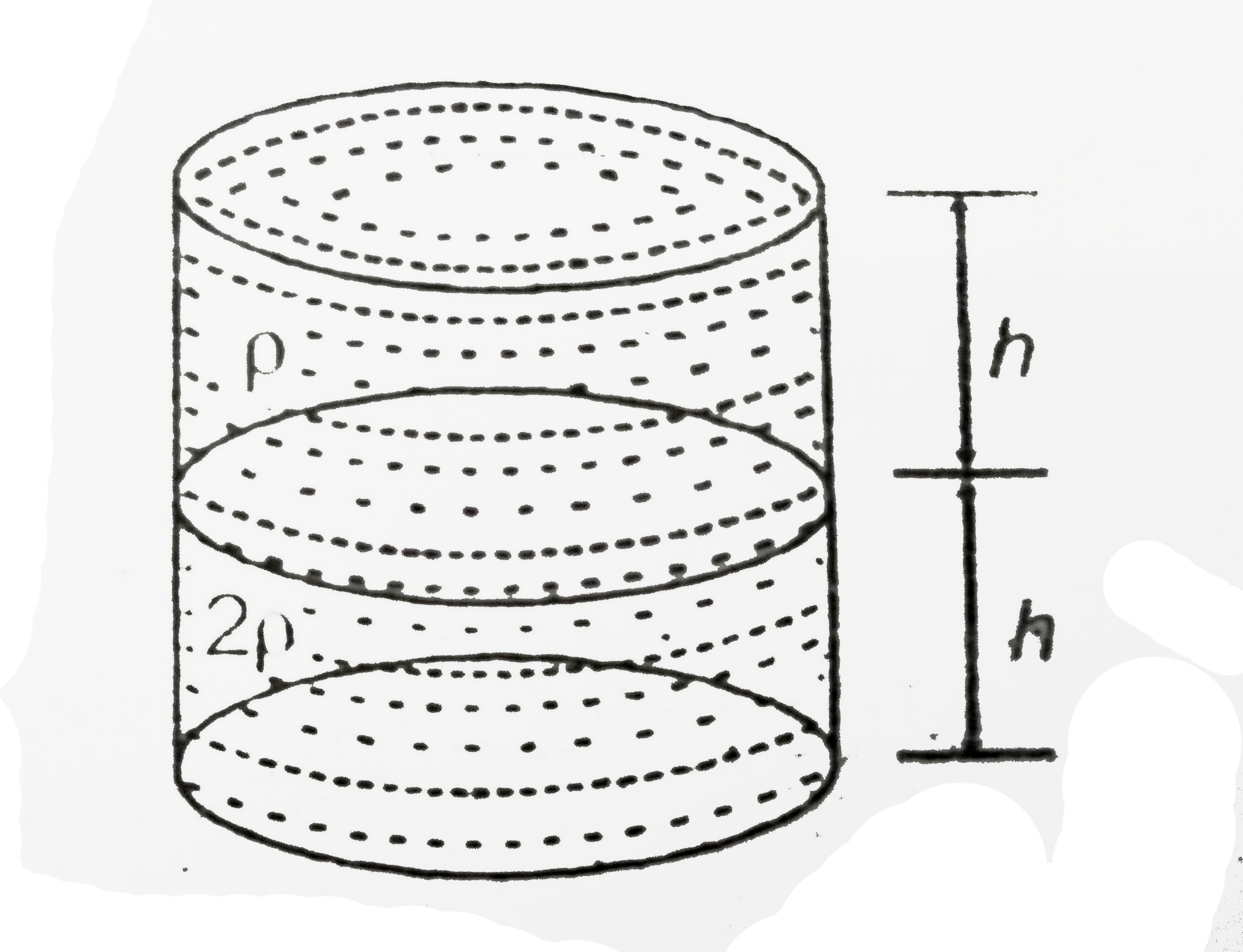
View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
View SolutionLet the area of the base of a cylinder be B and the height of the cylinder be h. Write a formula for the cylinder’s volume V.
View SolutionA cylinder of certain mass is held in vertical position. If the height of the cylinder is 10 cm and radius of cross - section is 4 cm such that the pressure acting on its bottom surface is 21560N m−2 , find the mass of the cylinder ?
View Solution

