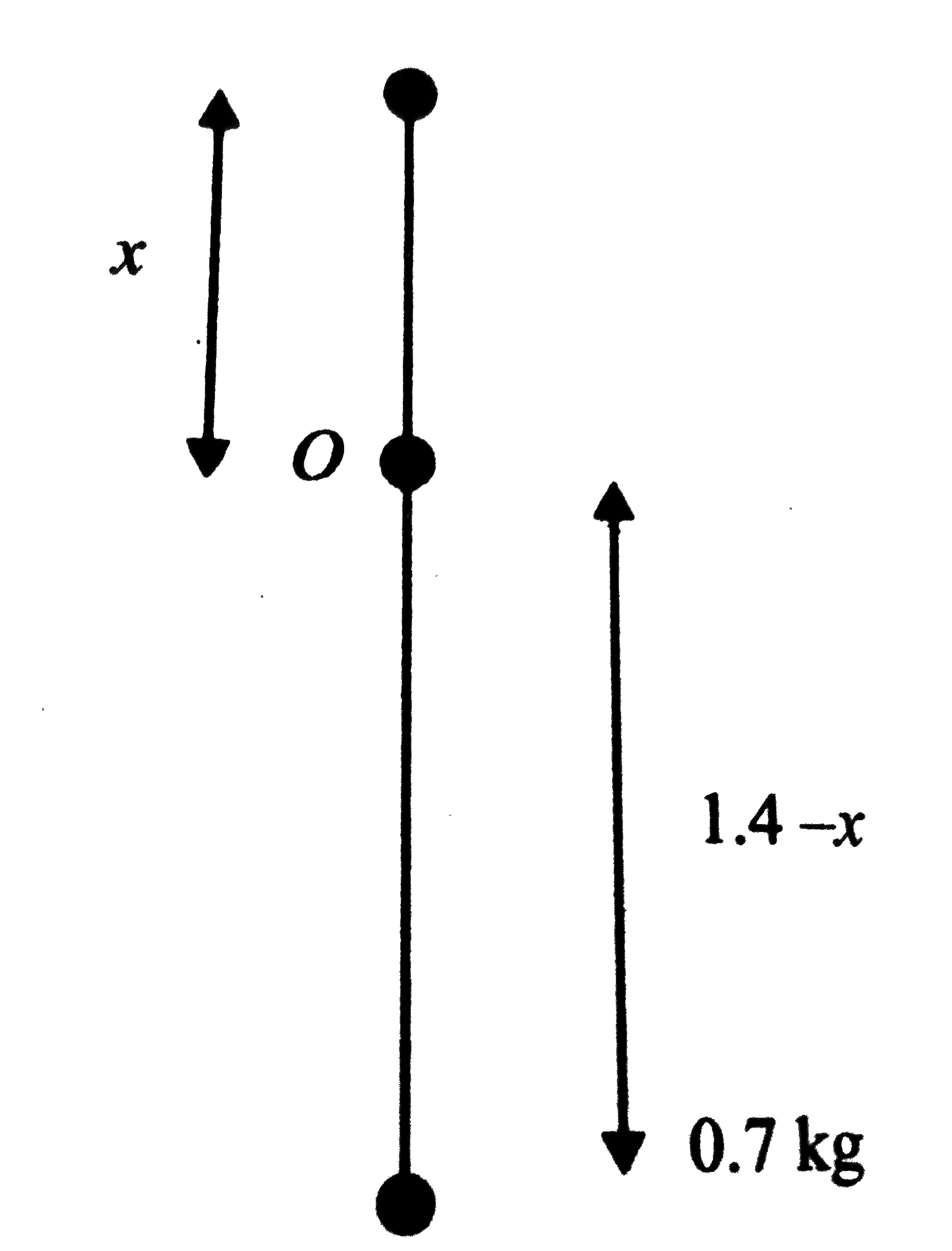
Two point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of

$0.42 m$ from the mass of $0.3 k g$

$0.70 m$ from the mass of $0.7 k g$

$0.98 m$ from the mass of $0.3 k g$

$0.98 m$ from the mass of $0.7 k g$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Two point masses $A$ of mass $M$ and $B$ of mass of $4 M$ are fixed at the ends of a rod of length $l$ and of negligible mass. The rod is set rotation about an axis perpendicular to its length with a uniform angular speed. The work required for rotating the rod will be minimum when the distance of axis of rotation from the mass $A$ is at
A $\frac{2}{5} l$
B $\frac{8}{5} l$
C $\frac{4}{5} l$
D $\frac{l}{5}$
Point masses $m_{1} and m_{2}$ are placed at the opposite ends of a rigid rod of length $L$ , and negligible mass. The rod is to be set rotating about an axis perpendicualr to it. The position of point $P$ on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity $ω_{0}$ is minimum, is given by :

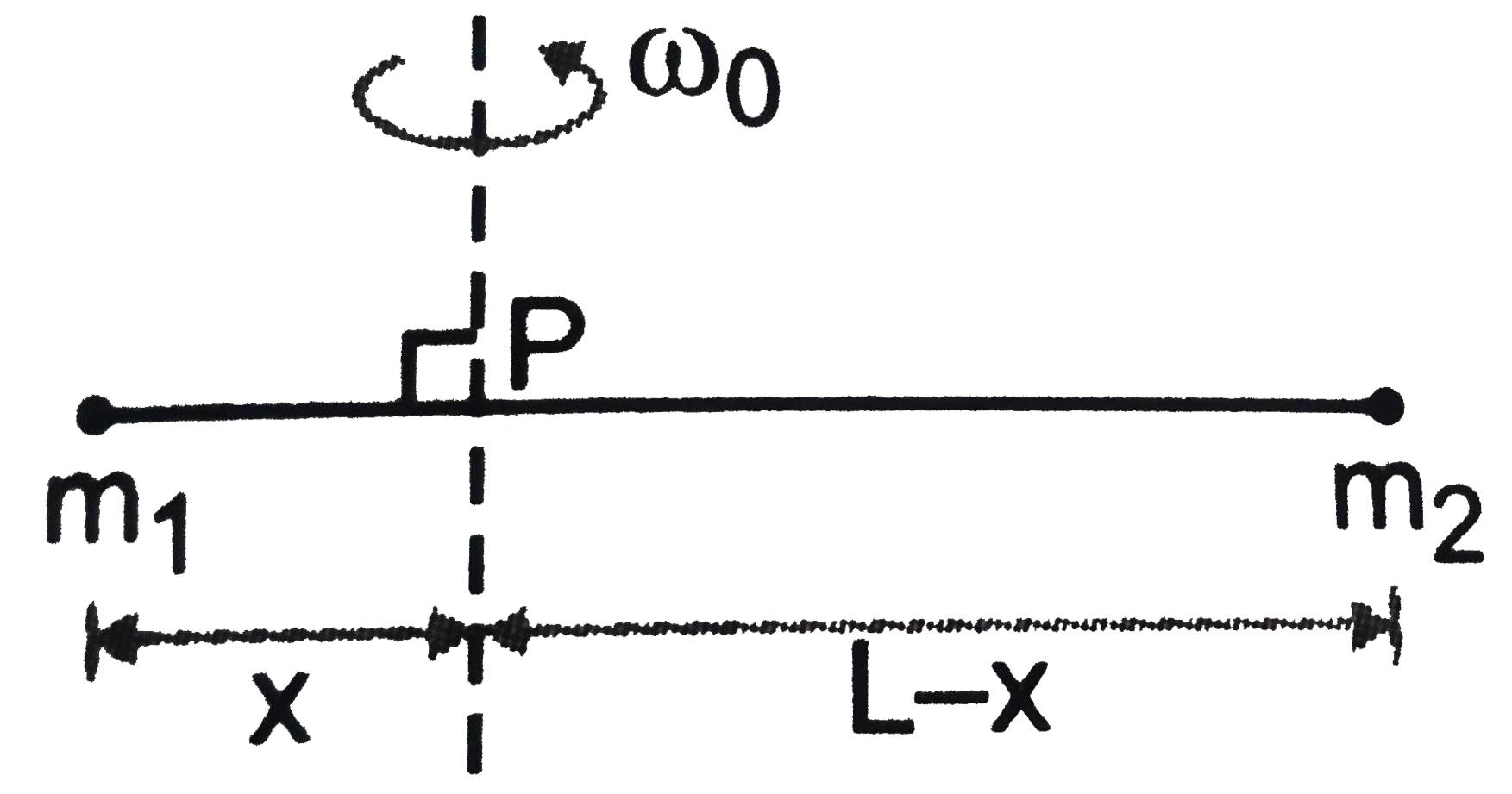A $x = \frac{m_{2} L}{m_{1} + m_{2}}$
B $x = \frac{m_{1} L}{m_{1} + m_{2}}$
C $x = \frac{m_{1}}{m_{2}} L$
D $x = \frac{m_{2}}{m_{1}} L$
Two small spheres of mass $5 k g$ and $15 k g$ are joined by a rod of length $0.5 m$ and of negligible mass. The $M . I .$ of the system about an axis passing through centre of rod and normal to it is
A $10 k g m^{2}$
B $1.25 k g m^{2}$
C $20 k g m^{2}$
D $8 k g m^{2}$