A force of magnitude F is acting on rolling body of mass m and radius R as show in figure. What happens when it enters on a smooth surface?

When the body is rolling on the rough surface, the friction force acting on the surface acts in the backward direction. The force F increases acceleration of centre of mass while friction force provides torque for providing angular acceleration. The velocity of centre of mass is always such that vc=ωR, i.e, rolling is present. when the body enters on the smooth surface, the pulling force F is still acting i.e., F≠0

When the rolling body enters on a smooth surface, the force of friction disappears, i.e, f=0. As a result angular acceleration of the body about its centre of mass becomes zero.
What ever is the angular speed attained by the body, it continues to rotate with that. On the conntrary, the linear acceleration of the centre of mass suddenly increases to Fm
As a result its linear speed starts increasing and the condition vc=ωR does not hold true and the body will not roll on the smooth surface. The point of contact slips forward (v>ω0R).
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A rolling body of mass m and radius R is rolling on a rough surface without any pulling force as shown in figure. What happens when it enters on a smooth surface?

View SolutionAt the instant t=0, a force F=kt (k is a constant) acts on a small body of mass m resting on a smooth horizontal surface. The time, when the body leaves the surface is
View Solution
Knowledge Check
The total energy of rolling of mass 'm' and radius 'R' is
A3/2mv2B1/2mv2Cmv2D5/2mv2When a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
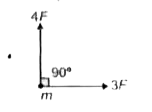 AaB2aC5aD8a
AaB2aC5aD8aA horizontal force F of variable magnitude and constant direction acts on a body of mass m which is initially at rest at a point O on a smooth horizontal surface. The magnitude of F is given by F=β+αt where t is the time for which the force has been acting on the distance of the body from O at time t , then s is equal to.
A12m(βt+αt2)tB12m(β+αt2)C(β+αt)t22mDt26m(3β+αt)
Two forces of equal magnitude F act on two isolated bodies P and Q as shown in the figure. The mass of body Q is three times that of body P. The magnitude of the acceleration of P is

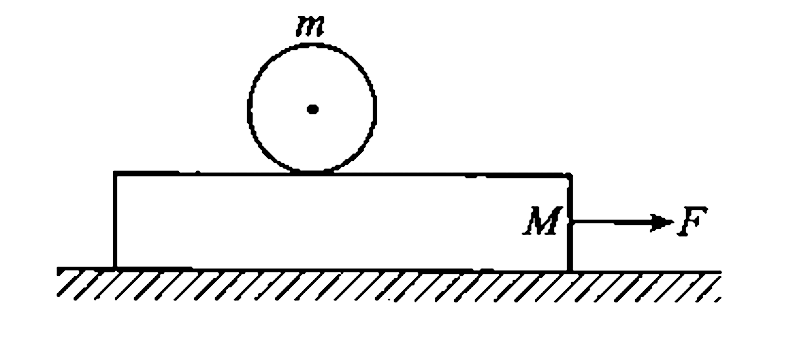
View SolutionA plank of mass M is placed on a smooth surface over which a cylinder of mass m and radius R is placed as shown in figure-5.63. Now the plank is pulled towards right with an external force F. If cylinder does not slip over the surface of plank find the linear acceleration of plank and cylinder and the angular acceleration of the cylinder.
View SolutionA force F acts at the centre of a thin spherical shell of mass m and radius R.
Find the acceleration of the shell if the surface is smooth.
View SolutionWhen a rolling body enters onto a smooth horizontal surface, it will
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View Solution
