In the figure, the block B of mass m starts from rest at the top of a wedge W of mass M. All surfaces are without friction. W can slide on the ground. B slides down onto the ground, moves along it with a speed v, has an elastic collision with the wall, and climbs back on to W.

From the beginning, till the collision with the wall, the centre of mass of 'B plus W' does not move horizontally.
After te collision, the centre of mass of B plus W moves with the velocity 2mvm+M
When B reaches its highest position of W, the speed of W is 2mvm+M
When B reaches its highest position of W, the speed of W is mvm+M
The correct Answer is:A, B, C, D
i. force acting on the horizontal direction is zero. Since block and wedge both are initially at rest. So velocity of COM (B plus W) does not move horizontally.
ii.vcm=mv−(−mv)M+m[∵vcm=mv1+m2v2m1+m2]
vcm=2mvM+m
ii When B reaches its highest position of W, the speed W is equal to velocity of COM i.e. v=2mvM+m
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Assertion - Reasoning
Explore 2 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Linked Comprehension
Explore 105 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Single Correct
Explore 141 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
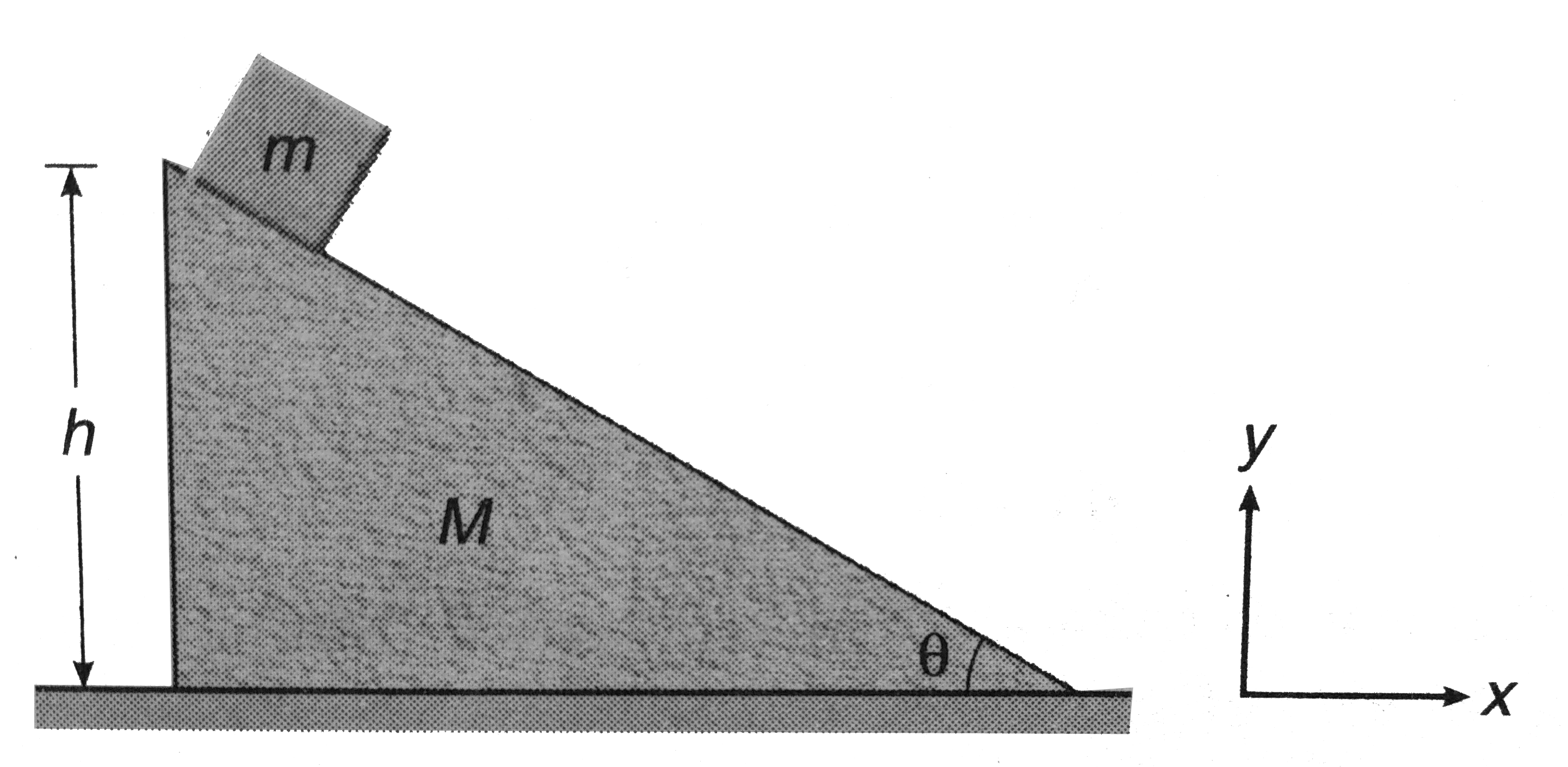
A block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
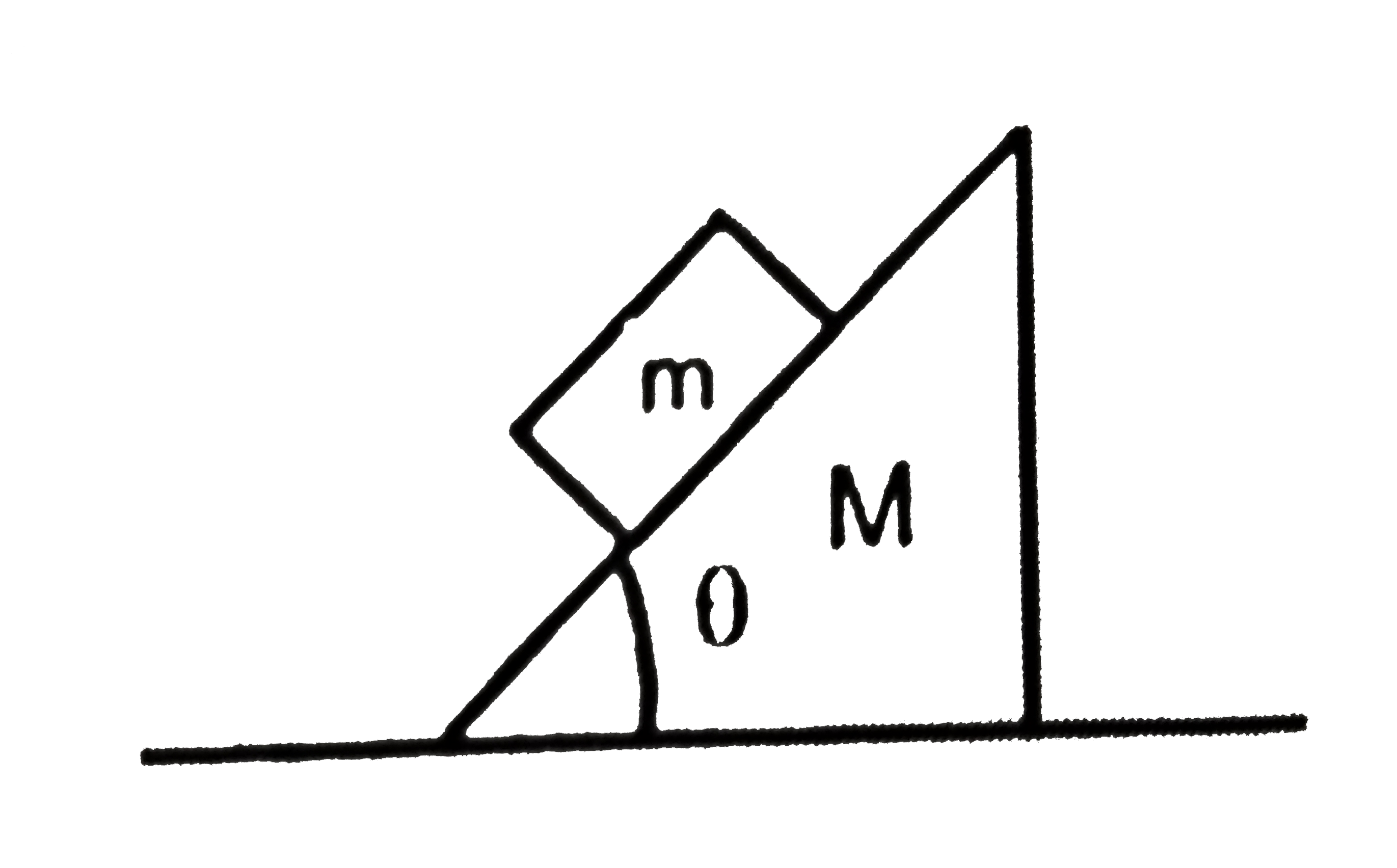
View SolutionA block of mass m lies on wedge of mass Mas shown in figure. Find the minimum friction coeffcient required between wedge Mand ground so that it does not move while block m slips down on it.
View Solution
Knowledge Check
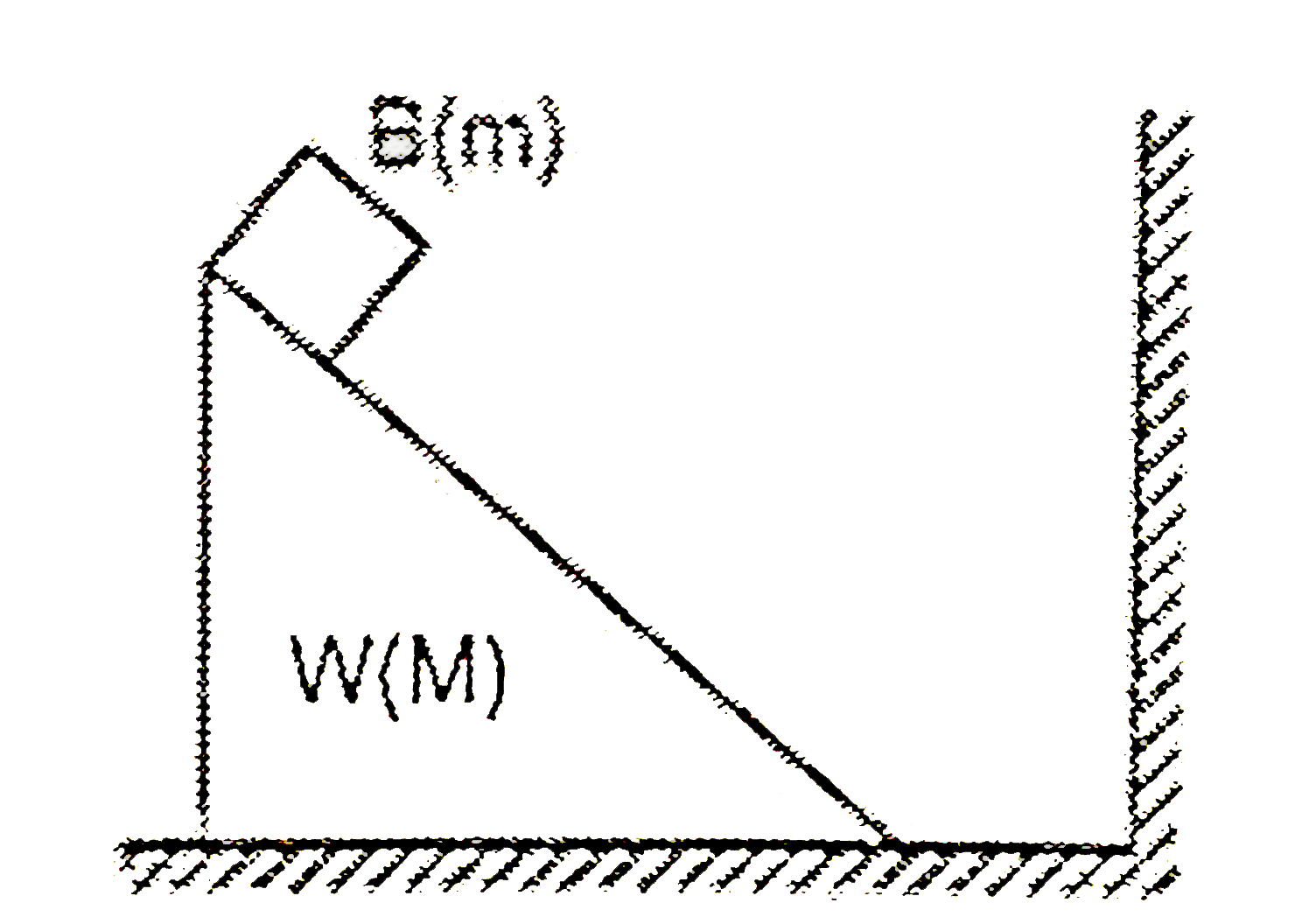
In the figure, the block B of mass m starts from rest at the top of a wedge W of mass M. All surfaces are without friction. W can slide on the ground. B slides down onto the ground, moves along it with a speed v, has an elastic collision with the wall, and climbs back two W.AB will reach the top of W againBFrom the beginning, till the collision with the wall, the centre of mass of B plus W' does not move horizontally.CAfter the collision the centre of mass of B plus W' moves with the velocity 2mvm+MDWhen B reaches its highest position on W, the speed of W is 2mvm+WA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
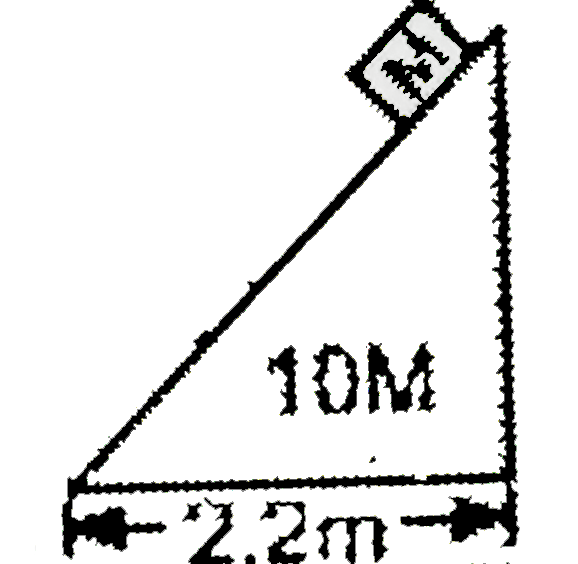 A0.22 mB0.20 mCzeroD0.24 m
A0.22 mB0.20 mCzeroD0.24 mA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest
 A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the above
A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the above
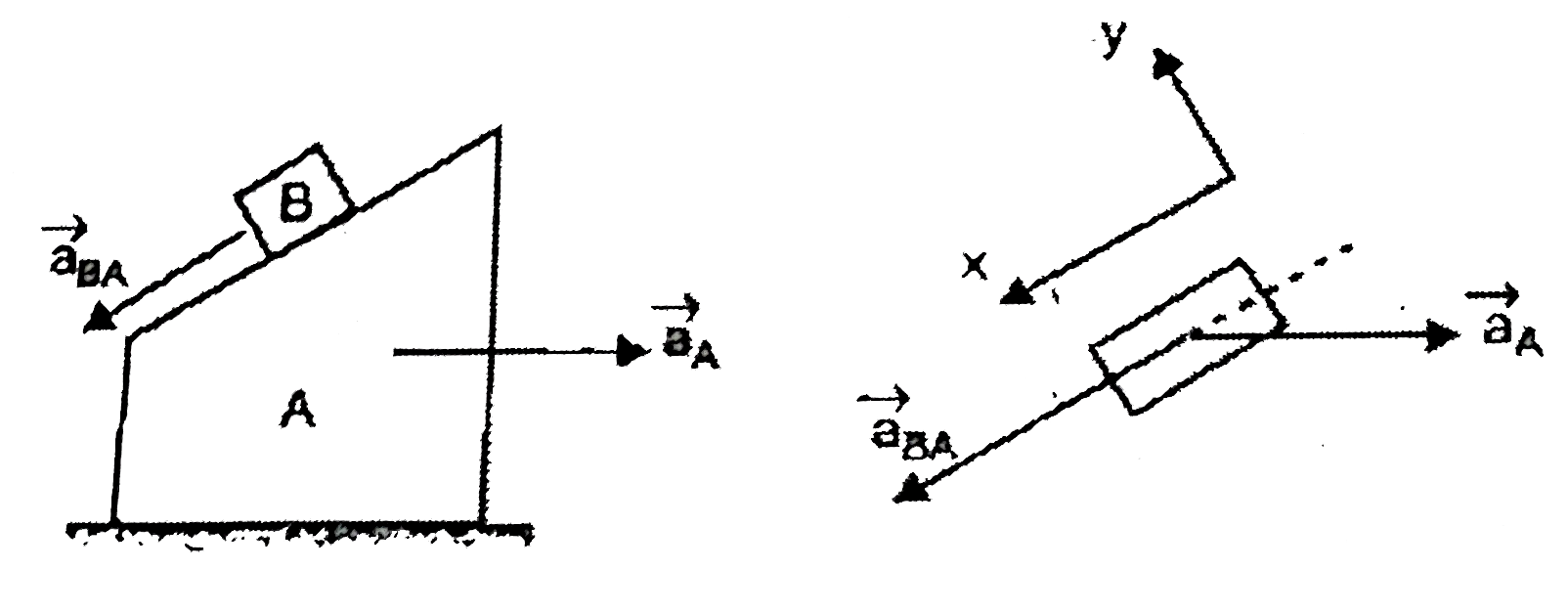
The block B starts from rest and slides on the wedge A which can move on a horizontal surface, Neglecting friction, determine (a) the acceleration of wedge, (b) the acceleration of the block relative to the wedge.
View SolutionA block of mass m is placed on hthe top of bigger wedge M. All the surfaces are frictionless. The system is released from rest. Find the distance moved by smaller block (w.r.t triangular wedge) when bigger wedge travles distance X on plane surface
_PHY_219_Q01.png)
View SolutionBlock B has mass m and is released from rest when it is on top of wedge A, which has a mass 3m. Determine the tension in cord CD needed to hold the wedge from moving while B is sliding down A. Neglect friction.

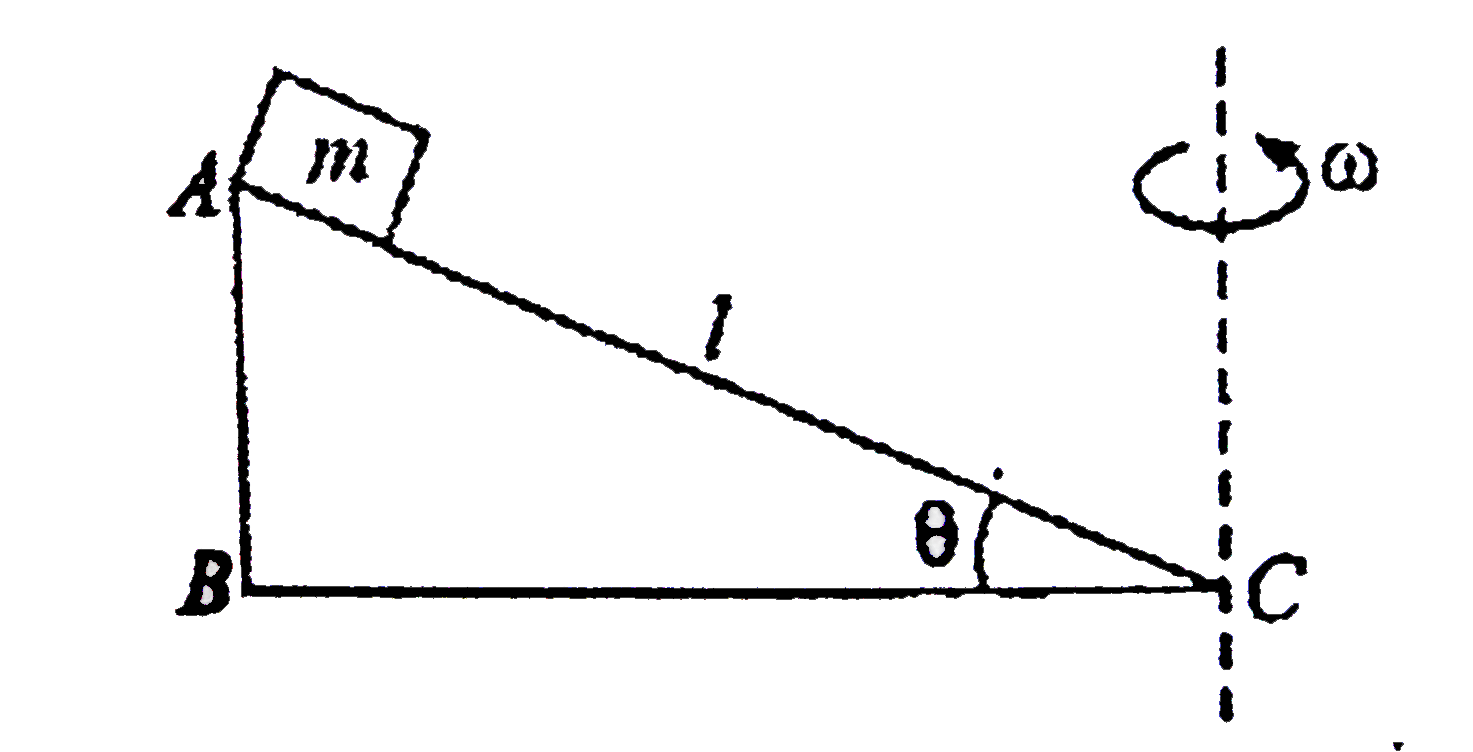
View SolutionA block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
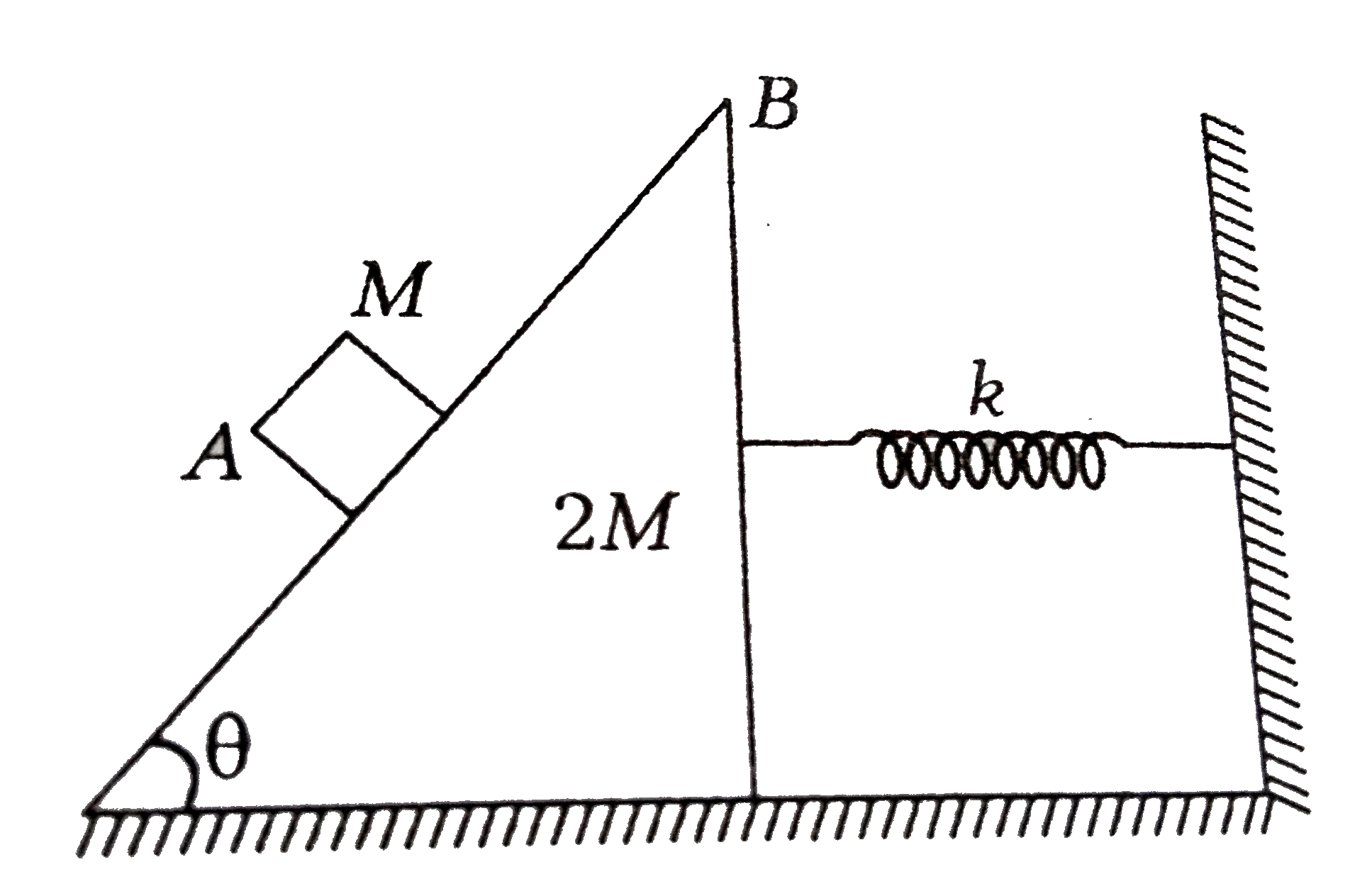
View SolutionA block A of mass M rests on a wedge B of mass 2M and inclination θ. There is sufficient friction between A and B so that A does not slip on B. If there is no friction between B and ground, the compression in spring is
View Solution

