Two wooden plank of mass M1=1kg,M2=2.98kg smooth surface. A bullet of mass m=20gm strikes the block M1 and pierces through it, then strikes the plank B and sticks to its. Consequently both the planks move with equal velocities. Find the percentage change in speed of the bullet when it escapes from the first block.
The correct Answer is:33.3%
Conservation of linear momentum of the system yield
Mv0=M1v+mv'=(M2+m)v
⇒v=mv0M2+m
and mv'=mv0−M1v
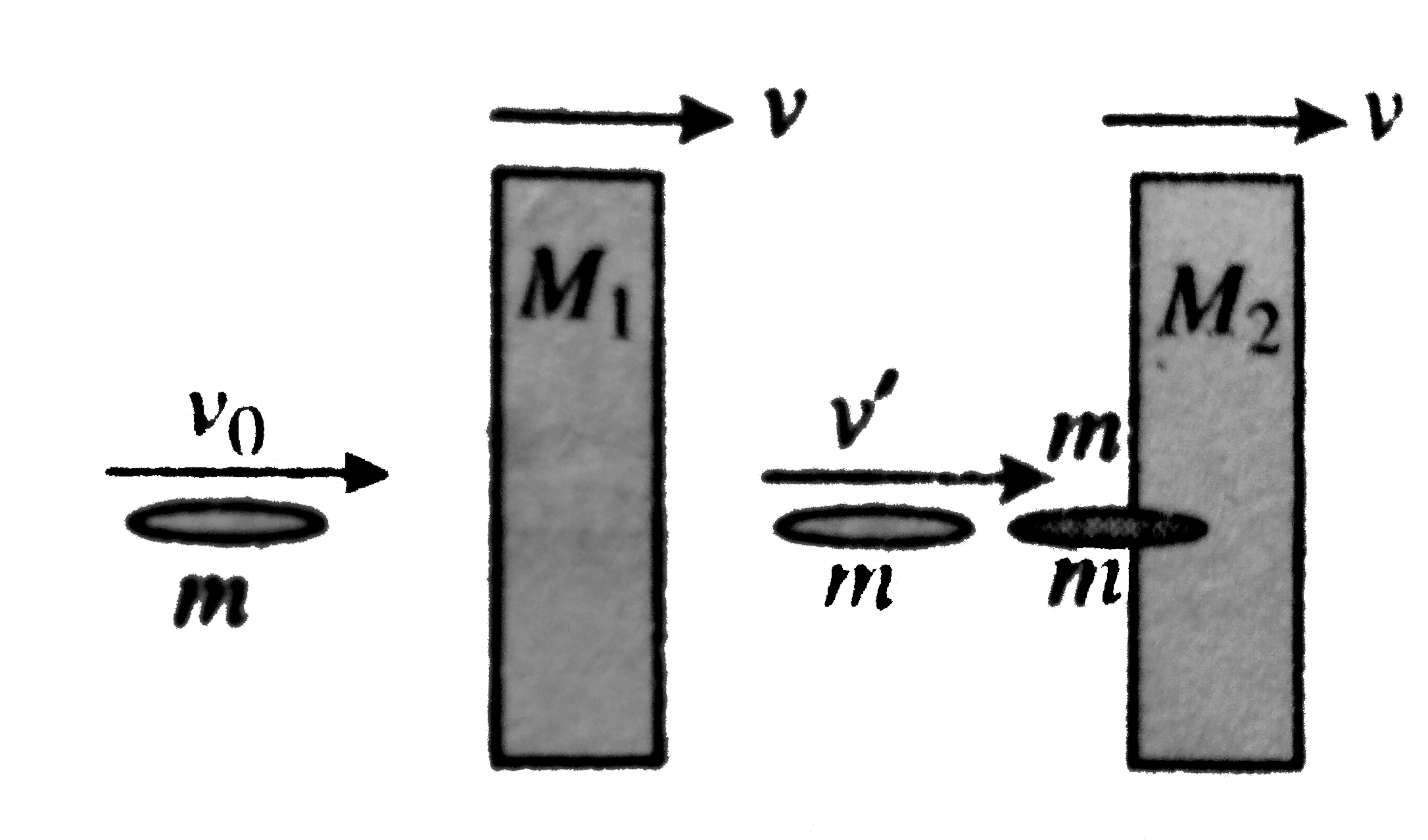
=mv0−M1mv0M2+m
=mv0[1−M1M2+m]
⇒v'=v0−v0M1M2+m
now find |v'−v0|v0×100=M1(M+m)×100=33.3%
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A m=20gm bullet pierces through a plate of mass M1=1kg and then comes to rest inside a second plate of massM2=2.98kg as shown in figure. It is found that the two plates, initially at rest, now move with equal velocities. Find the percentage loss in the initial velocity of the bullet when it is between M1andM2. Neglect any loss of material of the plates, due to the action ofthe bullet.
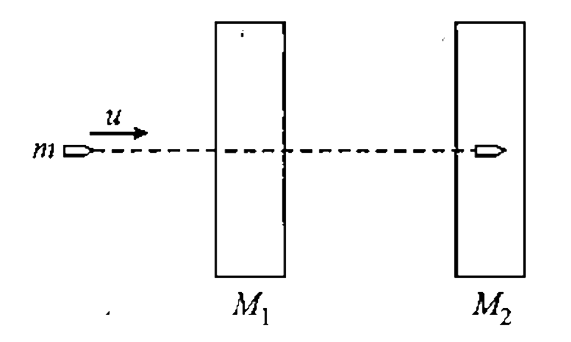
View SolutionTwo wooden blocks of masses 1kg and 2kg are separated by a certain distance A bullet of mass 50g fired from a gun pierces through the block of mass 1kg and then stopped in the second block After the impact of the bullet both blocks start moving with the same speed Calculate the percentage loss in the initial velocity of the bullet when it is inbetween the two blocks .
View Solution
Knowledge Check
A 20g bullet pierces through a plate of mass M1=1kg and then comes to rest inside a second plate of mass M2=2.98kg as shown in Fig. It is found that the two plates, initially at rest, now move with equal velocities. Find the percentage loss in the initial velocity of the bullet when it is between M1 and M2. Neglect any loss of material of the plates due to the action of bullet.
 A50%B25%C100%D75%
A50%B25%C100%D75%A 20 g bullet pierces through a plate of mass M1=1kg and then comes to rest inside a second plate of mass M2=2.98 kg as shown in the figure. It is found that the two plates, initially at rest, now move with equal velocities, Find the percentage loss in the initial velocity of the bullet when it is between M1andM2. Neglect any loss of material of the plates due to the action of bullet
 A50%B25%C100%D75%
A50%B25%C100%D75%A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2
A 20 gm bullet pierces through a plate of mass m1=1 kg and then comes to rest inside a second plate of mass M2=2.98 kg as shown , it is found that the two plates initily atrest , now move with equal velocity . Find the percentage loss in the initial velocity of the bullet when it is between M and M2 neglet any loss of material of the pletes due to the action of the bullet
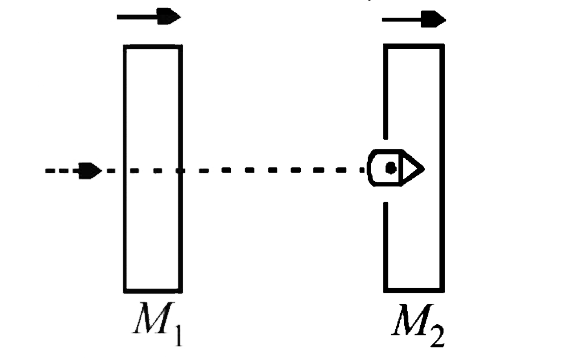
View SolutionA bullet of mass 0.1Kg moves with velocity 10ms it strikes a block and comes to rest after travels 0.5 m inside block. Find retardation of bullet
View SolutionA bullet of mass 0.1Kg moves with velocity 10ms it strikes a block and comes to rest after travels 0.5 m inside block. Find retardation of bullet
View SolutionA wooden plank of mass 20 kg is resting on a smooth horizontal floor. A man of mass 60 kg starts moving from one end of the plank to the other end. The length of the plank is 10 m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View SolutionA wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View Solution
