A pendulum bob of mass 10−2kg is raised to a height 5×10−2m and then released. At the bottom of its swing, it picks up a mass 10−3kg. To what height will the combined mass rise?
Velocity of pendulum bob in mean position
v1=√2gh=√2×10×5×10−2=1ms
when the bob picks up a mass 10−3kg at the bottom, then by conservation of liner momentum, the velocity of the coalesced mass is given by
m1v1+m2v2=(m1+m2)V
10−2×1+10−3×0=(10−2)+10−3()V
or V=1011m/s
if h' is the height risen by the combine mass, we have 12(m1+m2)V2=(m1+m2)gh'
∴h'=V22g=(1011)22×10m=5121m=0.413m
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A pendulum bob of mass 10−2kg is raised to a height 5×10−2m and then released. At the bottom of its swing, it picks up a mass 10−3kg. To what height will the combined mass rise?
View SolutionA pendulum bob of mass 10−2kg is raisted to hightof 5×10−2 m and then released At the bottion of its swing , it up a mass of 10−3 kg to what hieght will the combimnated mass rise ? Take g=10ms−2
View Solution
Knowledge Check
A body of mass 5 kg is raised vertically to a height of 10 m by a force 170 N. The velocity of the body at this height will be
A9.8 ms−1B15 ms−1C22 ms−1D37 ms−1The weight of a body of mass 3 kg at a height of 12.8×106 m from the surface of the Earth is ______.
A9.75 NB1.46 NC3.26 ND4.36 NA second's pendulum has a hollow spherical bob of mass 25×10−3kg. It is replaced by another solid bob of same radius but of mass 50×10−3kg. Then the new time period will be
A6sB4sC3sD2s
A bullet of mass 2g travelling at a speed of 500m/s is fired into a ballistic pendulum of mass 1.0kg suspended from a cord 1.0m long. The bullet penetrates the pendulum and emerges with a velocity of 100m/s. Through what vertical height will the pendulum rise?
View SolutionA pendulum bob of mass m and length L is released from angle θ with the vertical. Find
(a) the speed of the bob at the bottom of the swing and
(b) tension in the string at that time
View SolutionA body of mass 4kg, is taken from a height of 5 m to a height 10m. Find increase in potential energy.
View SolutionA body of mass 10kg is at height of 10m at point A as shown on a smooth track. Find speed at B.
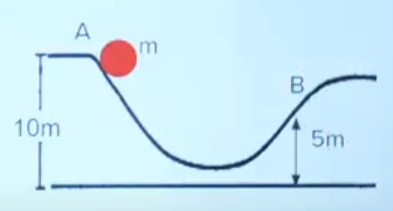
View SolutionA steel ball of mass 0.1 kg falls freely from a height of 10 m and bounces to a height of 5.4 m from the ground. If the dissipated energy in this process is absorbed by the ball, the rise in its temperature is (specific heat of steel =460K/kg∘/C,g=10m/s2)
View Solution
