A body of mass explodes at rest break up into three parts.If two parts having equal masses fly off perpendicularly to each other with a velocity of 18m/s, then calculate the velocilty of the third part which has a mass 3 times the mass of each part.
Initially the body is at rest. Initial linear momentum of the body is zero. Let due to explosion the body break up into three parts. There is no external force acting on the body. Hence linear momentum just after collision also be zero.
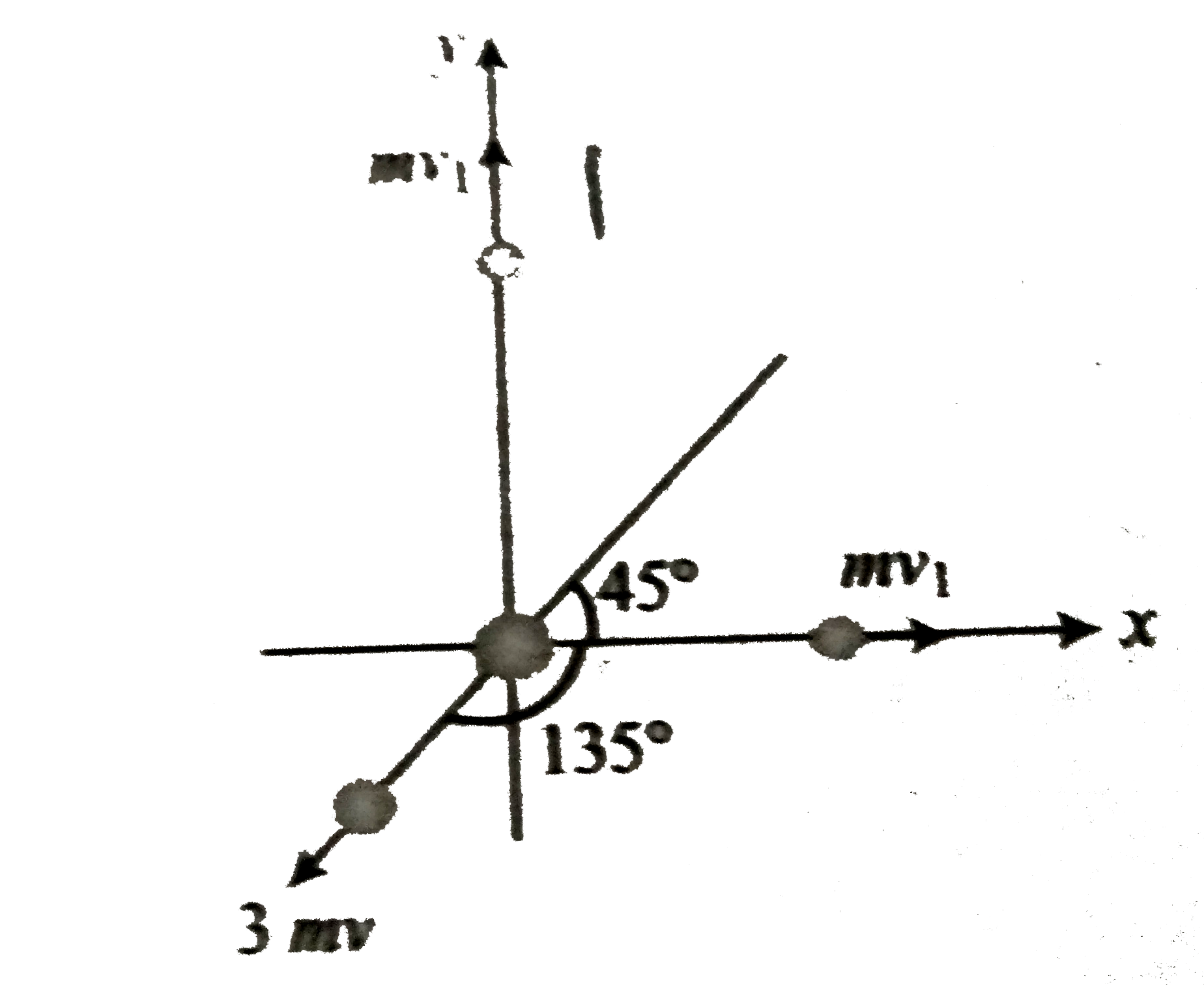
Let total mass of the body be 5cm, hence the masses of the broken parts will be m,m and 3m respectively.
→pinitial=0
Linear momentum just after explosion
→pfinal=→p1+→p2+→p3=mv1ˆi+mv1ˆj+→p3
As →pinitial=→pfinal⇒|→p3|=√2mv1⇒3mv=√2mv1
v=√2v13=√2×183=6√2ms−1
⇒6√2ms−1 at an angle 135∘ from the either ball.
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Solved Examples
Explore 13 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Exercise 1.1
Explore 20 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A bomb at rest explodes into three fragments of equal massses Two fragments fly off at right angles to each other with velocities of 9m/s and 12/s Calculate the speed of the third fragment .
View SolutionA 5kg shell kept at rest suddenly splits up into three parts. If two parts of mas 2kg each are found flying due north and east with a velocity of 5m/seach, what is the velocity of the third part after explosion.
View Solution
Knowledge Check
A body at rest breaks up into 3 parts. If 2 parts having equal masses fly off perpendicularly each after with a velocity of 12m/s when the velocity of the third part which has 3× mass of each part is
Au4√2m/s at an angle of 45∘ from each bodyB24√2m/s at angle of 135∘ from each bodyC6√2m/s at 135∘ from each bodyD4√2m/s at 135∘ from each bodyA body at rest breaks up into 3 parts. If 2 parts having equal masses fly off perpendicularly each after with a velocity of 12m/s when the velocity of the third part which has 3× mass of each part is
A4√2m/s at an angle of 45∘ from each bodyB24√2m/s at an angle of 135∘ from each bodyC4√2m/s at 90∘ from each bodyD4√2m/s at 135∘ from each bodyA 7 kg shell kept at rest suddenly splits up into three parts. If two parts of mass 3 kg each are found flying due north and cast with a velocity of 3 m/s each, what is the velocity of the third part after explosion ?
A9 m/s due north-eastB9√2m/s due south-eastC9√2 m/s due south-westD9√2 m/s due south-east
A body of mass 1kg initially at rest explodes and breaks into threee fragments of masses in the ration breaks into three fragments of masses in the ration 1:1:3. The two pieces of equal masses fly off perpendicular to each other with a speed of 30m/s each What is the velocity of heavier fragments ? .
View SolutionA 5 kg shell kept at rest suddenly splits up into three parts. If two parts of mass 2 kg each are found flying due north and east with a velocity of 5 m/s each, what is the velocity of the third part after explosion ?
View SolutionA body of mass 1kg initially at rest explodes and breaks into three parts of masses in the ration 1:2:3. If the two pieces of equal masses fly off perpendicular to each other with a speed of 30m/s The speed of third piece will be .
View SolutionA vessel at rest explodes breaking it into three pieces. Two pieces having equal mass fly off perpendicular to one another with the same speed of 30m/s. The third piece has three times the mass of each of the other two pieces. What is the direction (w.r.t. the pieces having equal masses) and magnitude of its velocity immediately after the explosion?
View SolutionA vessel at rest explodes breaking it into three pieces. Two pieces having equal mass fly off perpendicular to one another with the same speed of 30m/s . The third pieces has three times the mass of each other piece. What is the direction (w.r.t. the piece having equal masses) and magnitude of its velocity immediately after the explosion?
View Solution

