Conducting sphere of radius R1 is covered by concentric sphere of radius R2. Capacity of this combination is proportional to
R2−R1R1R2
R2+R1R1R2
R1R2R1+R2
R1R2R2−R1
The correct Answer is:D
To solve the problem of finding the capacity of a conducting sphere of radius R1 covered by a concentric sphere of radius R2, we will follow these steps:
Step 1: Understanding the System
We have a conducting sphere of radius R1 and a concentric outer sphere of radius R2. The inner sphere will have a charge +Q, and the outer sphere will have a charge −Q due to the nature of capacitors.
Step 2: Determine the Electric Potential
The electric potential V at a distance r from a charged sphere is given by:
V=14πϵ0Qr
For the inner sphere at radius R1, the potential V1 is:
V1=14πϵ0QR1
For the outer sphere at radius R2, the potential V2 is:
V2=−14πϵ0QR2
Step 3: Calculate the Potential Difference
The potential difference ΔV between the two spheres is given by:
ΔV=V1−V2=14πϵ0(QR1+QR2)
This simplifies to:
ΔV=Q4πϵ0(1R1+1R2)
Step 4: Relate Charge and Capacitance
The capacitance C of the system is defined by the relationship:
Q=CΔV
Substituting for ΔV:
C=QΔV=QQ4πϵ0(1R1+1R2)
This simplifies to:
C=4πϵ0(1R1+1R2)−1
Step 5: Final Expression for Capacitance
Using the formula for the sum of reciprocals:
1R1+1R2=R1+R2R1R2
Thus, we can express C as:
C=4πϵ0R1R2R1+R2
Conclusion
The capacity of the combination of the conducting sphere and the concentric sphere is proportional to:
C∝R1R2R1+R2
We have a conducting sphere of radius R1 and a concentric outer sphere of radius R2. The inner sphere will have a charge +Q, and the outer sphere will have a charge −Q due to the nature of capacitors.
The electric potential V at a distance r from a charged sphere is given by:
V=14πϵ0Qr
For the inner sphere at radius R1, the potential V1 is:
V1=14πϵ0QR1
For the outer sphere at radius R2, the potential V2 is:
V2=−14πϵ0QR2
The potential difference ΔV between the two spheres is given by:
ΔV=V1−V2=14πϵ0(QR1+QR2)
This simplifies to:
ΔV=Q4πϵ0(1R1+1R2)
The capacitance C of the system is defined by the relationship:
Q=CΔV
Substituting for ΔV:
C=QΔV=QQ4πϵ0(1R1+1R2)
This simplifies to:
C=4πϵ0(1R1+1R2)−1
Using the formula for the sum of reciprocals:
1R1+1R2=R1+R2R1R2
Thus, we can express C as:
C=4πϵ0R1R2R1+R2
The capacity of the combination of the conducting sphere and the concentric sphere is proportional to:
C∝R1R2R1+R2
Topper's Solved these Questions
- ELECTROSTATICSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTROSTATICSExercise:PRACTICE EXERCISE (Exercise 2 (MISCELLANEOUS PROBLEMS))
Explore 47 Videos
- ELECTROSTATICSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTROSTATICSExercise:MHT CET Corner
Explore 29 Videos
- ELECTROSTATICSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTROSTATICSExercise:MHT CET Corner
Explore 29 Videos
- ELECTRONS AND PROTONSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTRONS AND PROTONSExercise:MHT CET CORNER
Explore 19 Videos
- FORCEBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:FORCEExercise:Exercise 2 (Miscellaneous Problems)
Explore 19 Videos
Similar Questions
A conducting sphere of radius R carries a charge Q. It is enclosed by another concentric spherical shell of radius 2R. Charge from the inner sphere is transferred in infinitesimally small installments to the outer sphere. Calculate the work done in transferring the entire charge from the inner sphere to the outer one.
View SolutionA solid conducting sphere of radius R is surrounded by a concentric metallic shell of inner radius 2R and outer radius 3R. The shell is earthed. The inner sphere is connected to a switch S by a thin conducting wire through a small hole in the shell. By closing the switch S, the inner sphere is connected to a distant conducting sphere of radius R having charge Q. Find the charge that flows to earth through wire AB.
View Solution
Knowledge Check
A conducting sphere of radius r has a charge . Then .
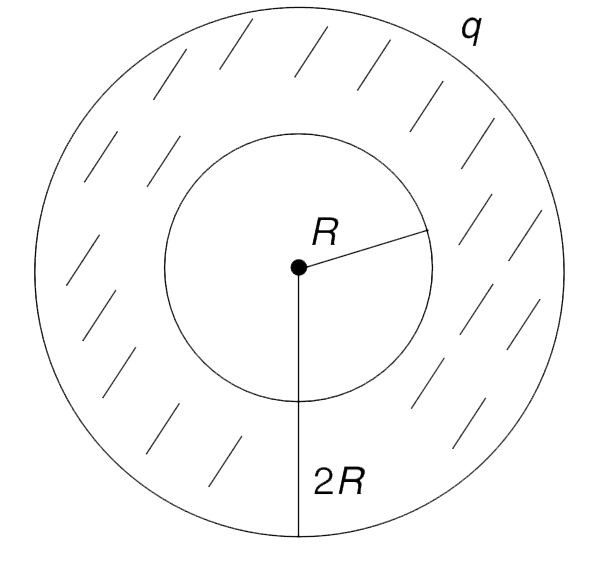
Athe charge is uniformly distributed over its surface if there is an external electric field .BDistribution of charge over its surface will be non uniform if no external electric field exist in space,CElectric field strength inside the sphere will be equal to zero only when no external electric field existsDPotential at every point of the sphere must be sameA charge q is distributed uniformly on the surface of a sold sphere of radius R. It covered by a concentric hollow conduction sphere of radius 2R. Find the charges inner and outer surface of hollow sphere if it is earthed.
 Aq2B2qC4qDZero
Aq2B2qC4qDZeroMetallic sphere of radius R is charged to potential V. Then charge q is proportional to
AVBRCbothDNone
A solid conducting sphere of radius R is surrounded by a concentric metallic shell of inner radius 2R and outer radius 3R. The shell is earthed. The inner sphere is connected to a switch S by a thin conducting wire through a small hole in the shell. By closing the switch S, the inner sphere is connected to a distant conducting sphere of radius R having charge Q. Find the charge that flows to earth through wire AB.

View SolutionThe volume of a sphere of radius 2r is
View SolutionA charge q is distributed uniformly on the surface of a sold sphere of radius R. It covered by a concentric hollow conduction sphere of radius 2R. Find the charges inner and outer surface of hollow sphere if it is earthed.

View SolutionThe capacitance of an isolated conducting sphere of radius R is proportional to
View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin unchanged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
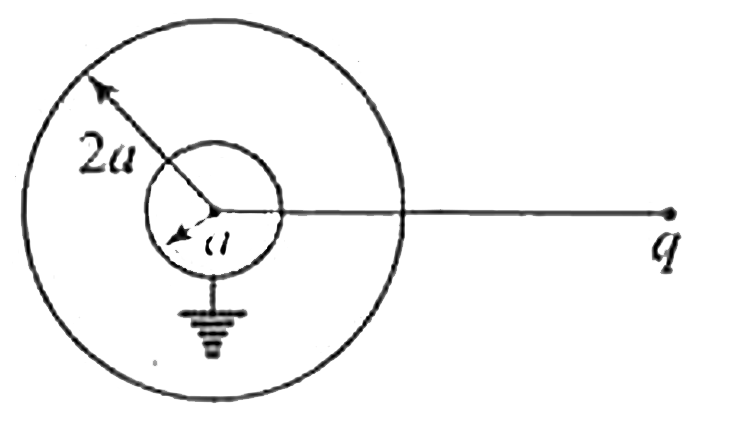
The charge on solid sphere is :
View Solution

