A charge Q is enclosed by a Gaussian spherical surface of radius R. If the radius is doubled, then the outward electric flux will
be reduced to half
remain the same
be doubled
increase four times
The correct Answer is:B
Total flux=Net enclosed chargeε0
Hence, we cany say the electric flux depends only on net enclosed charge by surface.
Topper's Solved these Questions
- ELECTROSTATICSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTROSTATICSExercise:PRACTICE EXERCISE (Exercise 2 (MISCELLANEOUS PROBLEMS))
Explore 47 Videos
- ELECTROSTATICSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTROSTATICSExercise:MHT CET Corner
Explore 29 Videos
- ELECTROSTATICSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTROSTATICSExercise:MHT CET Corner
Explore 29 Videos
- ELECTRONS AND PROTONSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTRONS AND PROTONSExercise:MHT CET CORNER
Explore 19 Videos
- FORCEBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:FORCEExercise:Exercise 2 (Miscellaneous Problems)
Explore 19 Videos
Similar Questions
A positive charge q is enclosed by a Guassian spherical surface of radius 'a' . If its radius is increased to 4a then the net outward flux will
View SolutionA charge Q is enclosed by a spherical Gaussian surface of radius R. If the radius of the sphere is double, how will the outward electric flux charge ? If a charge −Q is brought outside the Gaussian surface, will the electric flux reduce to zero ?
View Solution
Knowledge Check
Answer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
A charge q is enclosed by a Gaussian spherical surface of raidus R. If the radius is doubled then the electric flux will.Abe doubledBincreases four timesCbe reduced to half.Dremain the same.Consider a Gaussian spherical surface covering a dipole of charge q and -q, then
 Aq∈=0 (net charge enclosed by the spherical surface)Bϕ≠t=0 (net flux coming out the spherical surface)CE=0 at all points on the spherical surface.D∫→E⋅d→s = 0 (surface integral of over the spherical surface)
Aq∈=0 (net charge enclosed by the spherical surface)Bϕ≠t=0 (net flux coming out the spherical surface)CE=0 at all points on the spherical surface.D∫→E⋅d→s = 0 (surface integral of over the spherical surface)A charge q is enclosed by an imaginary Gaussian surface.

If radius of surface is increasing at a rate drdt=K, thenAflux linked with surface is increasing at a rate dϕdt=KBflux linked with surface is decreasing at a rate dϕdt=−KCflux linked with surface is decreasing at a rate dϕdt=1KDflux linked with surface is qε0
A charge Q is enclosed by a Gaussian surface. If surface area is doubled and charge Q is tripled then the outward electric flux will
View SolutionDefine electric flux. Write its SI unit. A charge q is enclosed by a spherical surface of radius R. If the radius is reduced to half, how would the electric flux through the surface change ?
View SolutionA charge q is enclosed as shown below the electric flux is

View SolutionAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surfance of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surfce is .

View SolutionA charge q is enclosed as shown, below the electric flux is
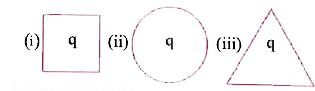
View Solution