Two identical radiators have a separation of $d = λ / 4$ where $λ$ is the wavelength of the waves emitted by either source. The initial phase difference between the sources is $λ / 4$ . Then the intensity on the screen at a distant point situated at an angle $θ = 30^{\circ}$ from the radiators is (here $I_{0}$ is intensity at that point due to one radiator alone)

$I_{0}$

$2 I_{0}$

$3 I_{0}$

$4 I_{0}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The intensity at a point on screen is given by
$I = 4 I_{0} {cos}^{2} (ϕ / 2)$
When $ϕ$ is the phase difference. In this problem $ϕ$ arises
(i) due to initial phase differnce of $\frac{π}{4}$ and (ii) due to path difference for the observation point situated at $θ = 30^{\circ}$ .
Thus,
$ϕ = \frac{π}{4} + \frac{2 π}{λ} (d sin θ) = \frac{π}{4} + \frac{2 π}{λ} \times \frac{λ}{4} ({sin 30}^{\circ}) = \frac{π}{4} + \frac{π}{4} = \frac{π}{2}$
Hence, $\frac{π}{2} = \frac{π}{4} and I = 4 I_{0} {cos}^{2} (\frac{π}{4}) = 2 I_{0}$

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Two identical sources each of intensity $I_{0}$ have a separation $d = λ / 8$ , where $λ$ is the wavelength of the waves emitted by either source. The phase difference of the sources is $π / 4$ The intensity distribution $I (θ)$ in the radiation field as a function of $θ$ Which specifies the direction from the sources to the distant observation point P is given by
A $I (θ) = I_{0} {cos}^{2} θ$
B $I (θ) = \frac{I_{0}}{4} {cos}^{2} (\frac{π θ}{8})$
C $I (θ) = 4 I_{0} {cos}^{2} [\frac{π}{8} (sin θ + 1)]$
D $I (θ) = I_{0} {sin}^{2} θ$
Question 2 - Select One
Two point monochromatic and coherent sources of light of wavelength $λ$ are each placed as shown in the figure below. The initial phase difference between the sources is zero. Select the incorrect statement.

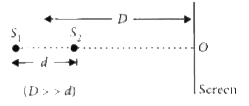AIf $d = \frac{7 λ}{2}$ , O will be minima
BIf $d = λ$ , only one maxima can be observed on screen .
CIf d=4.8 $λ$ , then total 10 minimas would be there on screen.
DIf $d = \frac{5 λ}{2}$ , then intensity at O would be maximum.
Question 3 - Select One
Two points nonochromatic and coherent sources of light of wavelength $λ$ each are placed as shown in figure. The initial phase difference between the sources is zero O. $(d > > d)$ . Mark the correct statement(s).

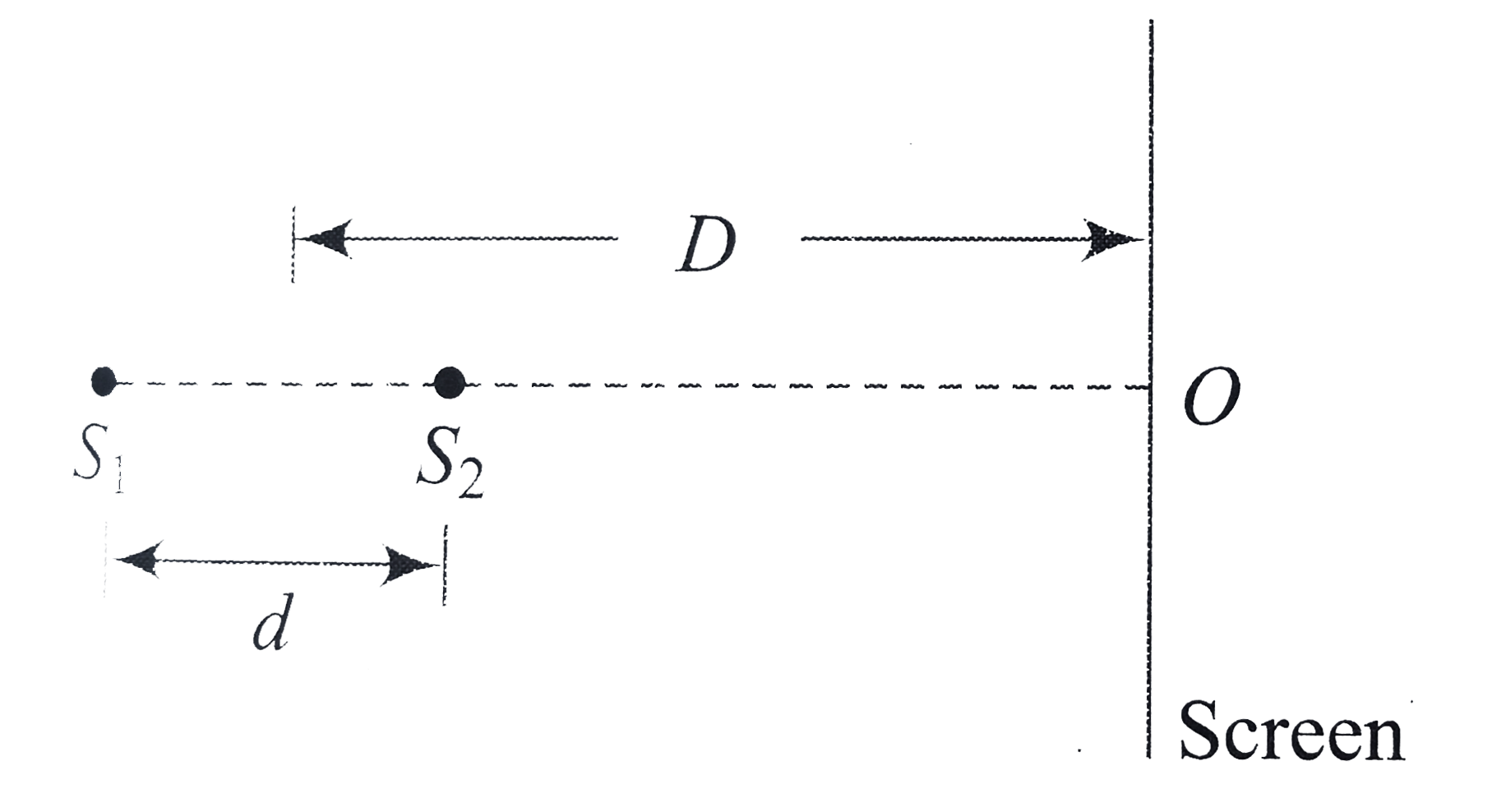AIf $d = \frac{7 λ}{2}$ , O will be a minima
BIf $d = λ$ , only one maxima can be observed on the screen
CIf $d = 4.8 λ$ , then total 10 minima would be there on the screen
DIf $d = \frac{5 λ}{2}$ , the intensity at O would be minimum.

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-INTERFERENCE AND DIFFRACTION OF LIGHT -Exercise 2 (MISCELLANEOUS PROBLEMS)

Home
Ask Doubt
Profile

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two point monochromatic and coherent sources of light of wavelength λ are each placed as shown in the figure below. The initial phase difference between the sources is zero. Select the incorrect statement.

Two points nonochromatic and coherent sources of light of wavelength λ each are placed as shown in figure. The initial phase difference between the sources is zero O. (d>>d). Mark the correct statement(s).

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-INTERFERENCE AND DIFFRACTION OF LIGHT -Exercise 2 (MISCELLANEOUS PROBLEMS)

Two point monochromatic and coherent sources of light of wavelength $λ$ are each placed as shown in the figure below. The initial phase difference between the sources is zero. Select the incorrect statement.

Two points nonochromatic and coherent sources of light of wavelength $λ$ each are placed as shown in figure. The initial phase difference between the sources is zero O. $(d > > d)$ . Mark the correct statement(s).