In an interference pattern the position of zeroth order maxima is 4.8 mm from a certain point P on the screen. The fringe width is 0.2 mm. The position of second maxima from point P is
5.1 mm
5 mm
40 mm
5.2 mm
The correct Answer is:A
The distance between zeroth order maxima and second order minima is
y1=β2+β=32β=320×0.2mm=0.3mm
∴ The distance of second minima from point P is
y=(4.8+0.3)mm=5.1mm
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHT BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHT EXERCISE - Exercise 2 (MISCELLANEOUS PROBLEMS)
40 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHT BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHT EXERCISE - MHT CET Corner
24 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHT BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHT EXERCISE - MHT CET Corner
24 Videos
- GRAVITATION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - GRAVITATION EXERCISE - MHT CET Corner
20 Videos
- KINETIC THEORY OF GASES ANDRADIATIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - KINETIC THEORY OF GASES ANDRADIATIONEXERCISE - MHT CET Corner
40 Videos
Similar Questions
In Lloyd's mirror experiment (Fig.) a light wave emitted directly be the source S (narrow slit) interferes with the wave reflected form a mirror M. As s result, an interference fringe pattern is

formed on the screen Sc. the source and the mirror are separated by a distance l=100cm.At a certain position of the source the fringe width on the screen was equal to Δx=0.25mm, and after source was moved away from the mirror plane by Δh=0.60mm, the fringe width decreased η=1.5 times. Find the wavelength of light.
View SolutionIn Young's double-slit experment, the frist maxima is observed at a fixed point P on the screen. Now, the screen is continously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (center of the screen)

View Solution
Knowledge Check
In an interference pattern produced by using a biprism, the zeroth order maxima is at a distance of 4.7mm from a point P on the screen. If the fringe width is 0.2 mm, then the distance of the second minima from the point P will be
Aonly 4.4 mmBonly 5 mmCeither 4.4 mm or 5 mm depending upon the position of PD6 mmIn interference of light, β is fringe width. The distance of nth maxima from the centre of interferene pattern is
Axnn.βBxn=(2n−1)β2Cxn=βnDxn=n2.βTwo sources give interference pattern which is observed on a screen, D distance apart from the sources. The fringe width is 2 w . If the distance D is now doubled, the fringe width will
ABecome w /2BRemain the sameCBecome wDBecome 4 w
In Young's double slit experiment, an interference pattern is obtained on a screen by a light of wavelength 6000Å, coming from the coherent sources S1 and S2. At certain point P on the screen third dark fringe is formed. Then the path difference S1P−S2P in microns is
View SolutionIn a Lloyds's mirror experiment as narraow slit S iransmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.

If fringe width is 0.1 mm then what is the wavelength of light used ?
View SolutionIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. Angular position of a bright fringe of order 5 when the screen is at position (1), will be nearly

View SolutionIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. When the screen is at position (1), phase difference of waves from S1 and S2 at point P is effectively.

View SolutionIn a Lloyds's mirror experiment as narraow slit S iransmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
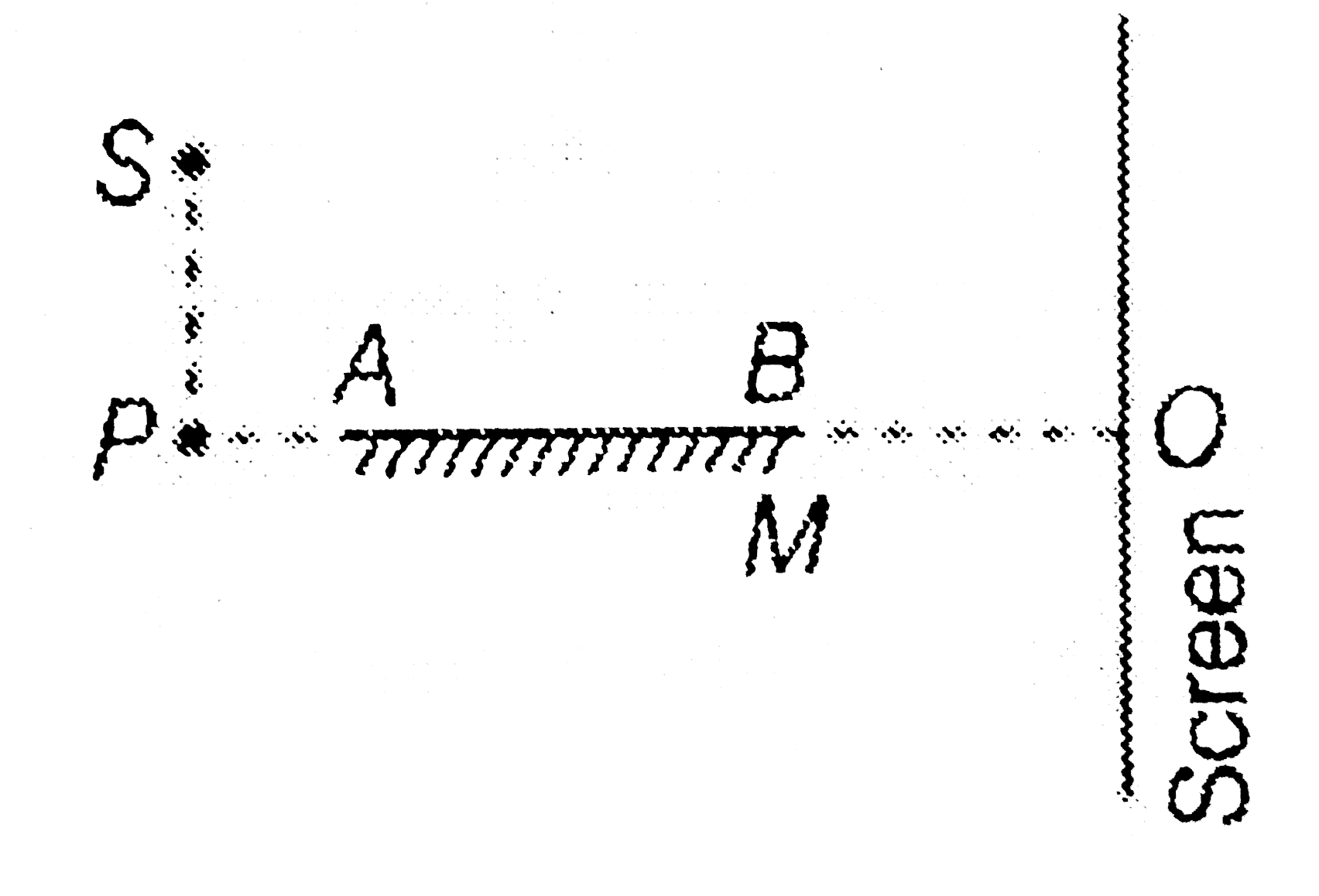
If the mirror is shifted towards left then how does the fringe pattern on screen changes ?
View Solution
