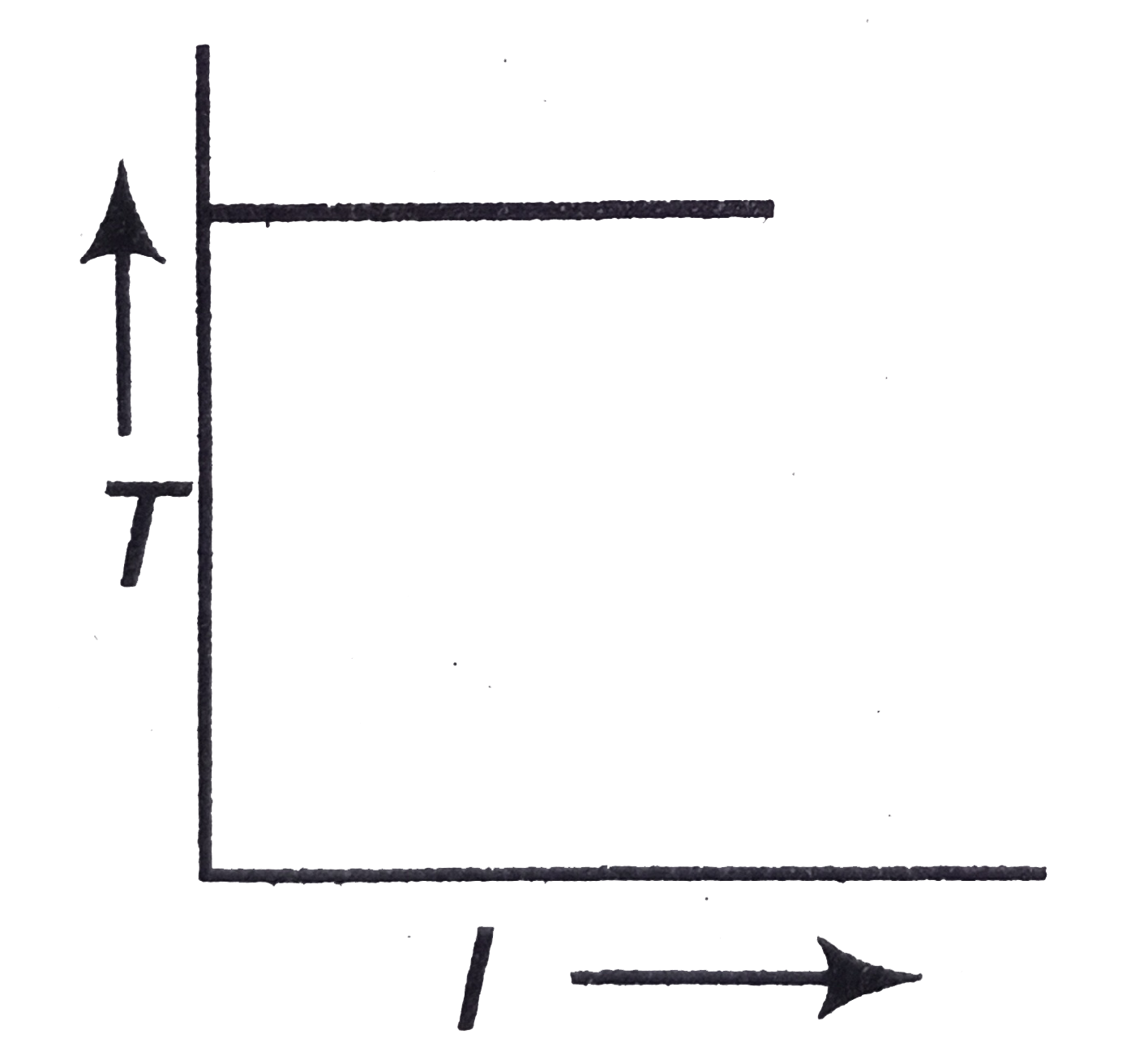
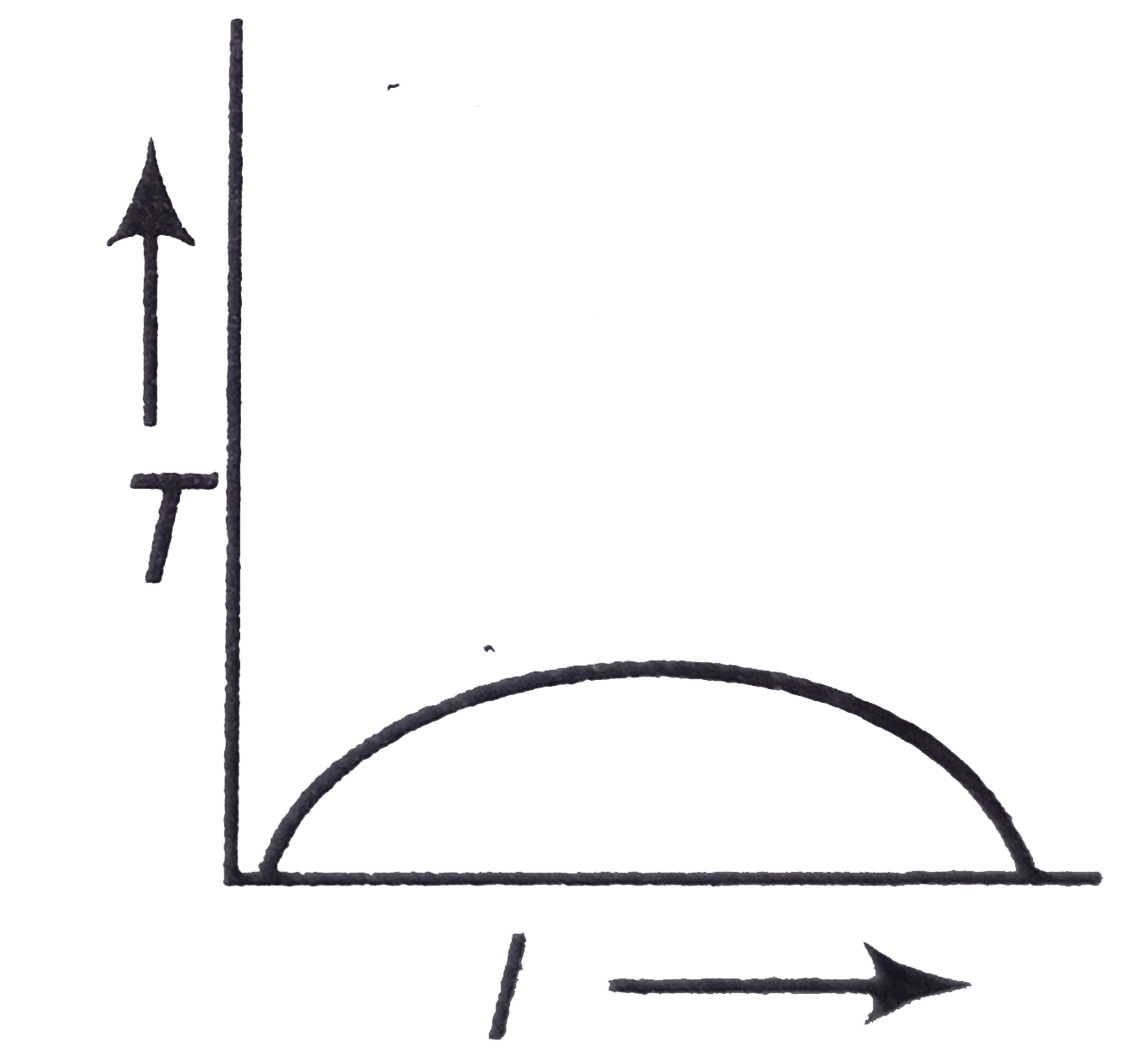
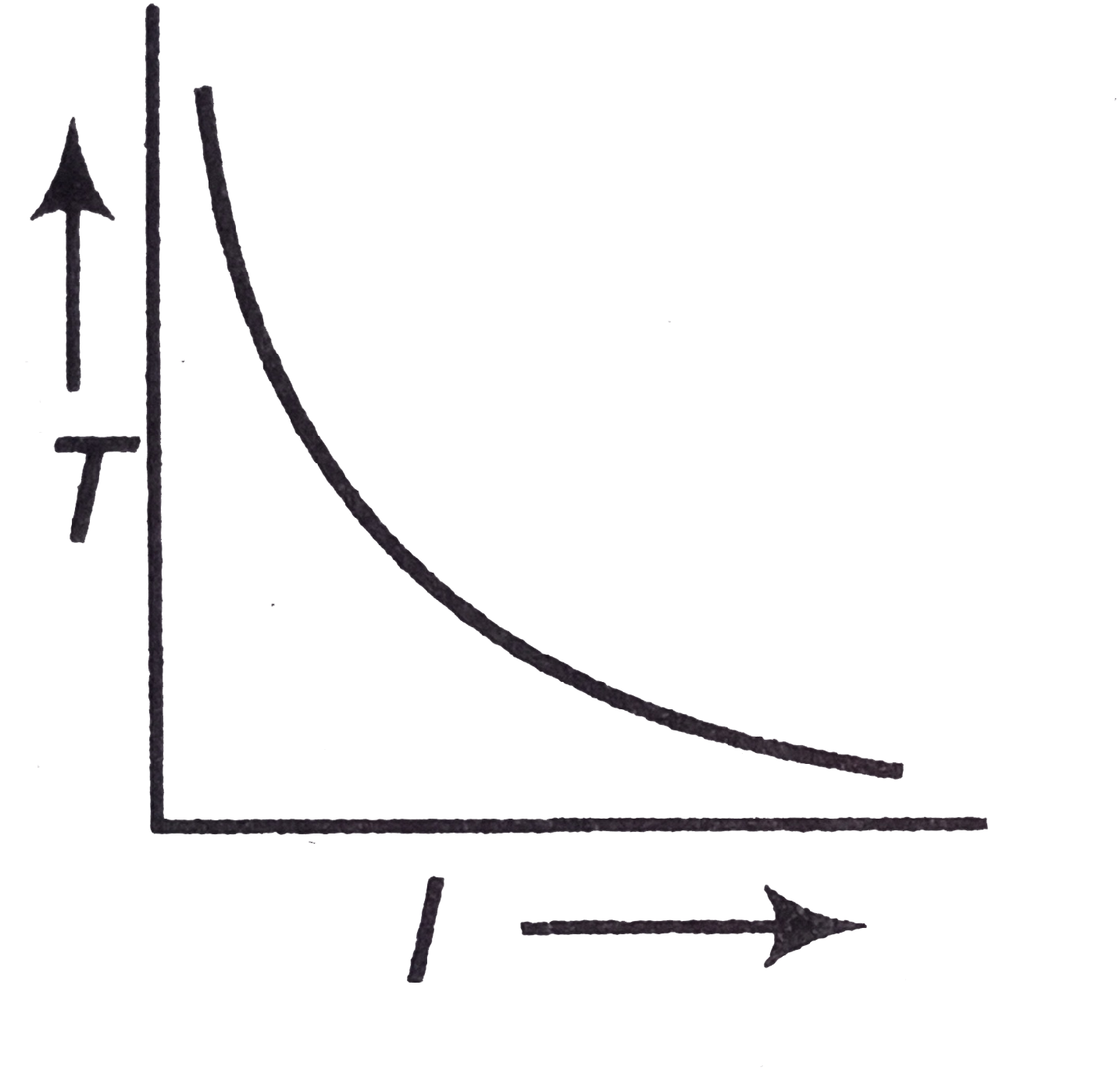
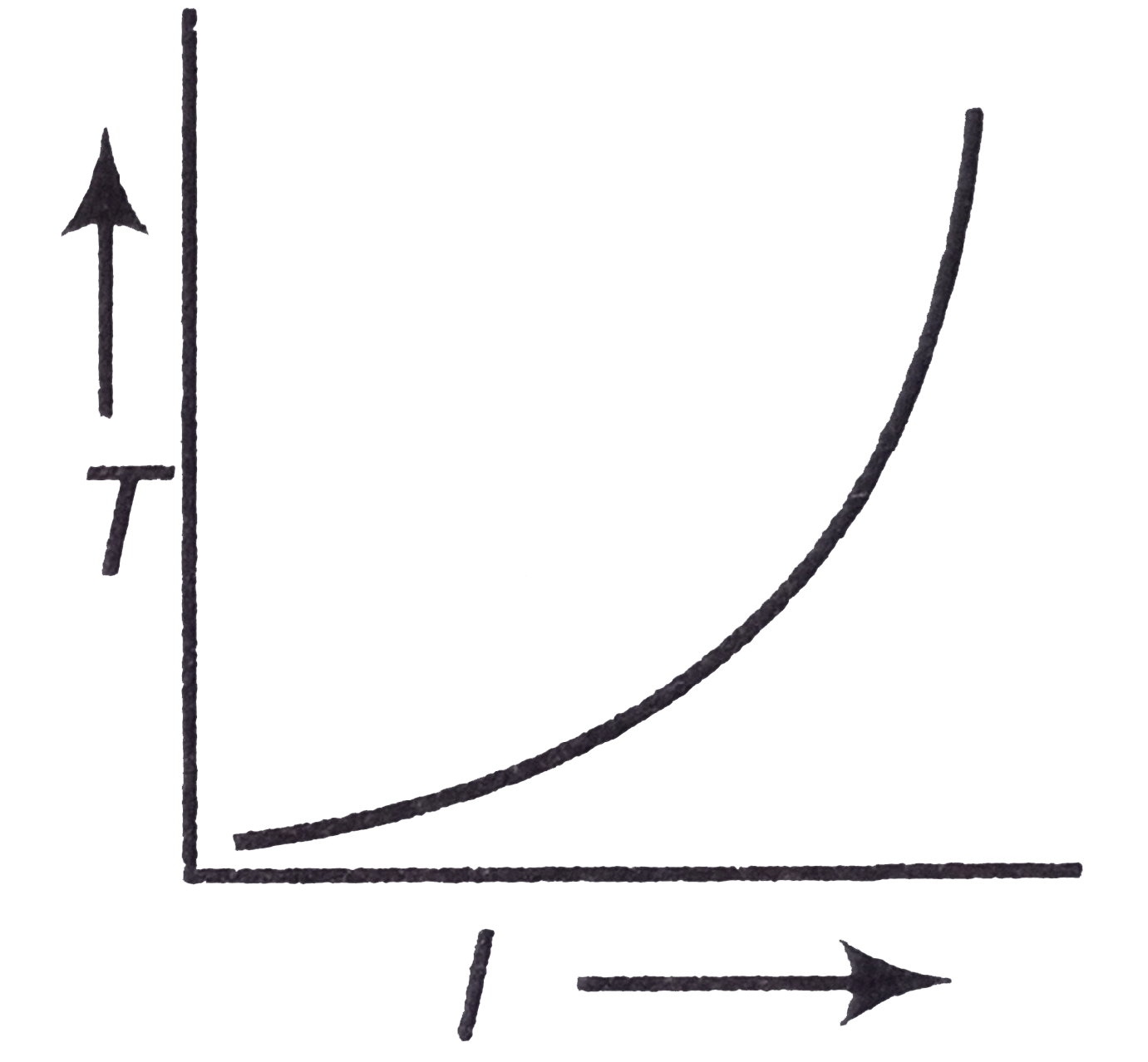
In case of a simple pendulum, time period versus length is depicted by
A
B
C
D
Video Solution
Text Solution
The correct Answer is:B
T=2π√IgorT2∝l
i.e. T - I graph is a parabola.
|
Topper's Solved these Questions
- OSCILLATIONSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:OSCILLATIONSExercise:EXERCISE 2
Explore 49 Videos
- OSCILLATIONSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:OSCILLATIONSExercise:MHT CET CORNER
Explore 29 Videos
- OSCILLATIONSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:OSCILLATIONSExercise:MHT CET CORNER
Explore 29 Videos
- MOCK TEST 5Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:MOCK TEST 5Exercise:MCQs
Explore 42 Videos
- PRACTICE SET 01Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PRACTICE SET 01Exercise:PAPER 1 (PHYSICS & CHEMISTRY)
Explore 50 Videos
Similar Questions
Knowledge Check
Time period of simple pendulum is
AT=2π√lgBT=2π√glCT=√2πlgDT=12π√glAn amplitue of a simple pendulum of a period 'T' and length 'L' is increased by 5%. The new period of that pendulum will be
AT8BT4CT2DTThe period of a simple pendulum is double, when its length is increased by 1.2 m. The original length of the simple pendulum is
A0.2 mB0.3 mC0.4 mD0.5 m
The time period of a simple pendulum is 2s. It its length is increased by 4 times, then its period becomes
View SolutionThe time period of a simple pendulum of infinte length is
View SolutionIn the case of a simple pendulum, a graph is drawn between the displacement and time taken for its oscillations as shown in the figure. Then
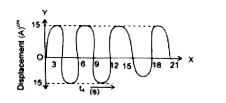
Time period of the pendulum bob is ______ s.
View SolutionThe time period of oscillation of a simple pendulum is √2s. If its length is decreased to half of initial length, then its new period is
View SolutionThe time period of simple pendulum is T. If its length is increased by 2%, the new time period becomes
View Solution

