A bob of mass m suspended by a light inextensible string of length 'l' from a fixed point. The bob is given a speed of √6gl. Find the tension in the string when string deflects through an angle 120∘ from the vertical.
By COE theorem,
u=√6gl
12μ2=mg(1−cos120)+12mv2
gives v=√3gl
At point B, T+mgcos60∘=mv2l
But putting v=√3gl, we get,
T=52mg

Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.5
Explore 15 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.3
Explore 26 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A bob of mass m is suspended by a light inextensible string of length l from a fixed point such that it is free to rotate in a vertical plane. The bob is given' a speed of √4gl horizontally. The, height of the bob from the lower most point where the string just becomes slacked is nl3. Find n.
View SolutionA particle is suspended by a light vertical inelastic string of length 1 from a fixed support. At its equilbrium position it is projected horizontally with a speed √6gl. Find the ratio of the tension in the string in its horizontal position to that in the string when the particle is vertically above the point of support.
View Solution
Knowledge Check
An iron ball of mass m, suspended by a light inextensible string of length l from a fixed point O, is shifted by θ0 as shown so as to strike the vertical wail perpendicularly.The maximum angle made by the string with vertical after the first collision, if e is the coefficient of restitution, is
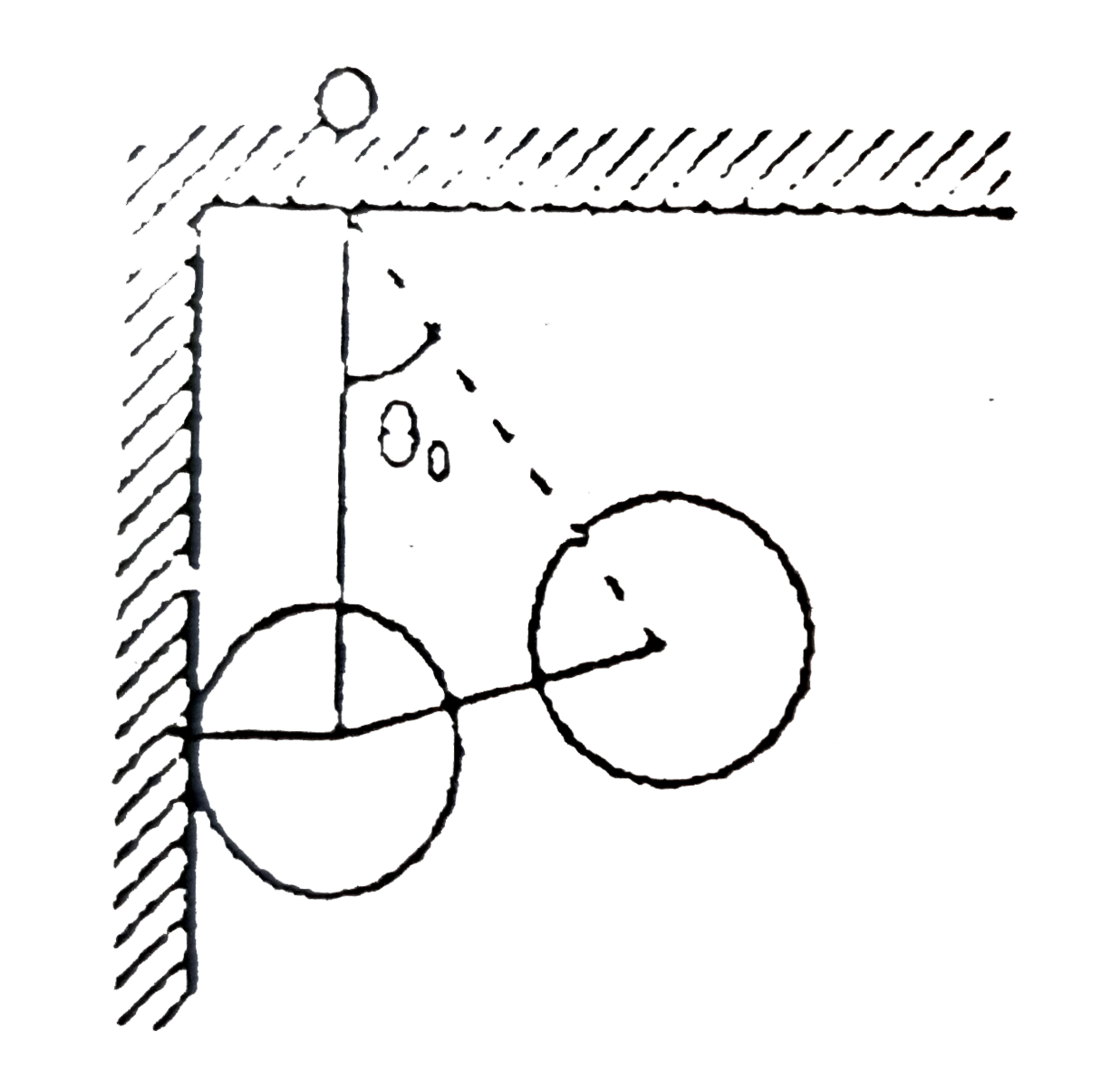 Asin−1{1−e2(1−cosθ0)}Bcos−1{1−e2(1−cosθ0)}Ctan−1{1−e2(1−cosθ0)}Dzero
Asin−1{1−e2(1−cosθ0)}Bcos−1{1−e2(1−cosθ0)}Ctan−1{1−e2(1−cosθ0)}DzeroA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
A√glB√2glC√3glD√gl3A particle suspended by a light inextensible thread of length l is projected horizontally from its lowest position with velocity √7gl/2. The string will slack after swinging through an angle equal to
A30∘B90∘C120∘D150∘
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. Particle is imparted a horizontal velocity u=√2gl. Find the angle made by the string with the vertical when the acceleration of the particle is inclined to the string by 45∘?
View SolutionA bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
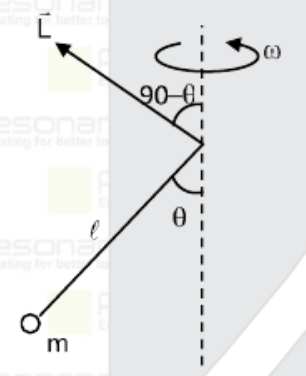
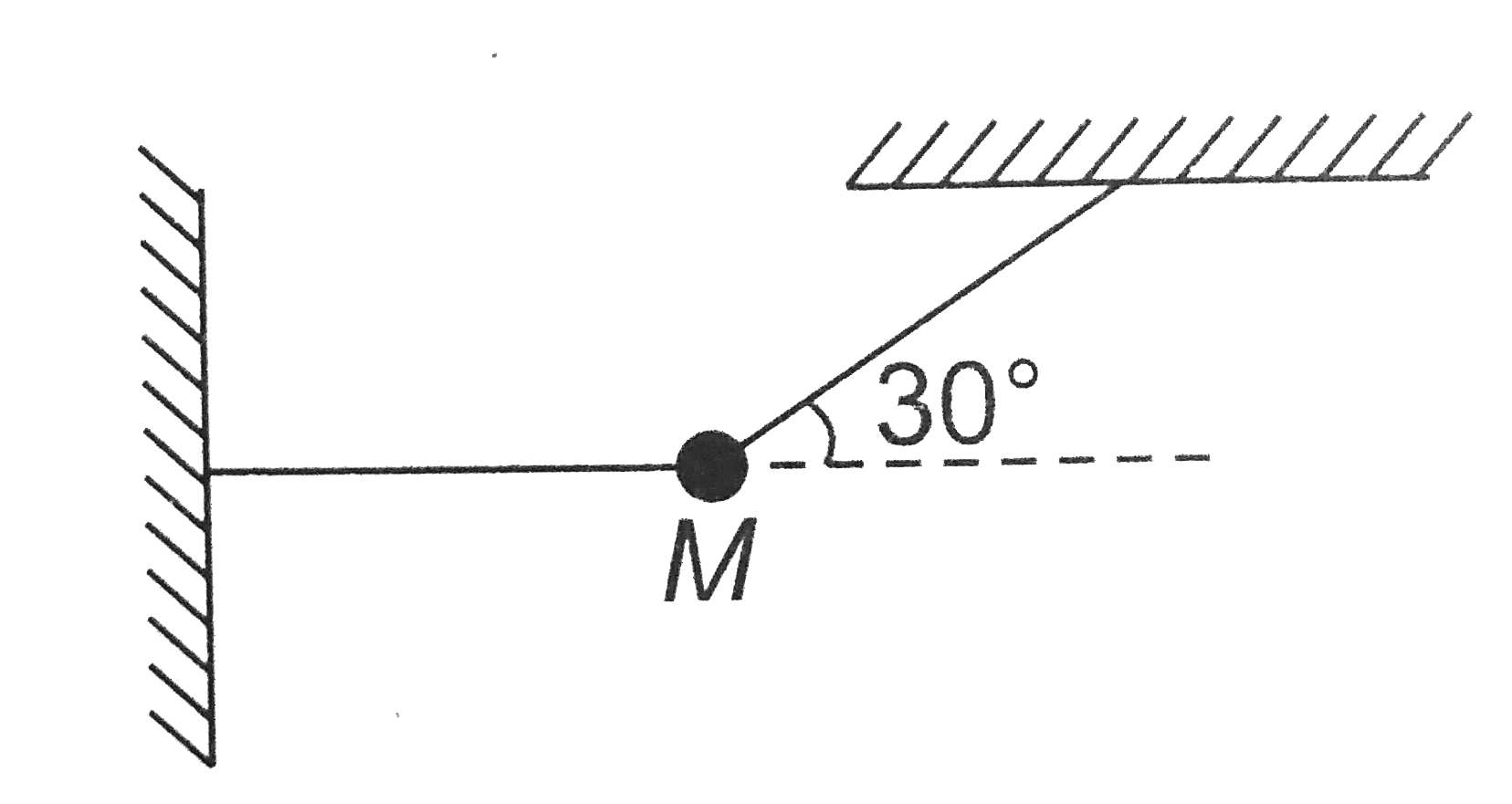
View SolutionA mass M is hung with a light inextensible string. Tension in horizontal part of string is.
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View Solution

