A coin is pushed down tangentially from an angular position θ on a cylindrical surface , with a velocity v as shown in figure If the coefficient of friction the coin and surface is μ find the tangential acceleration of the coin
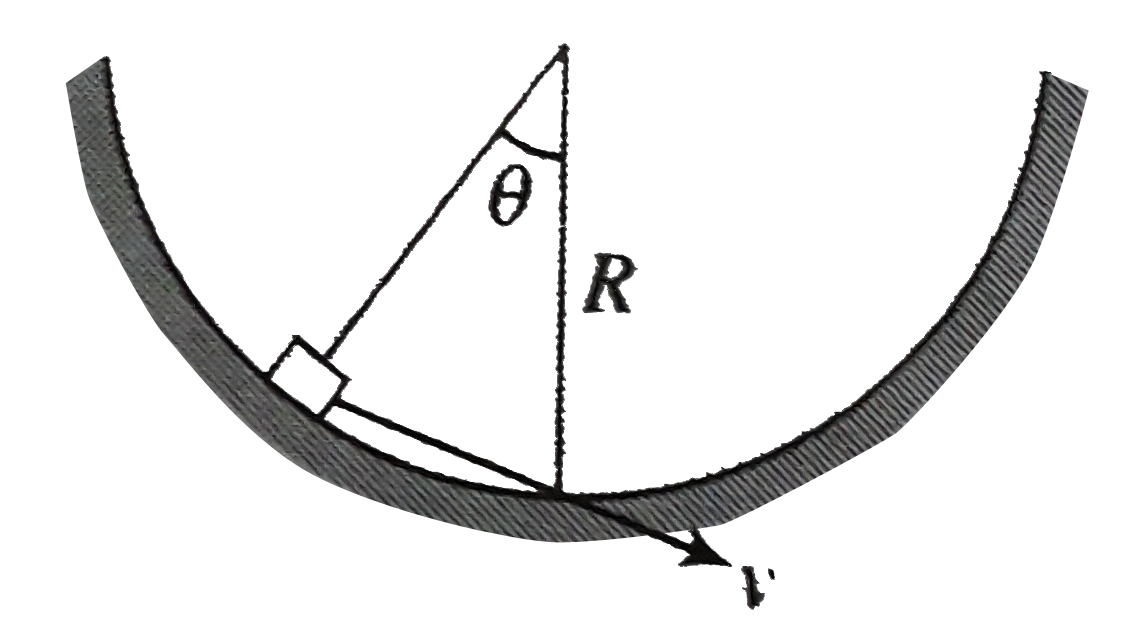
As the coin slides down, friction is kinetic and acts up along tha plane
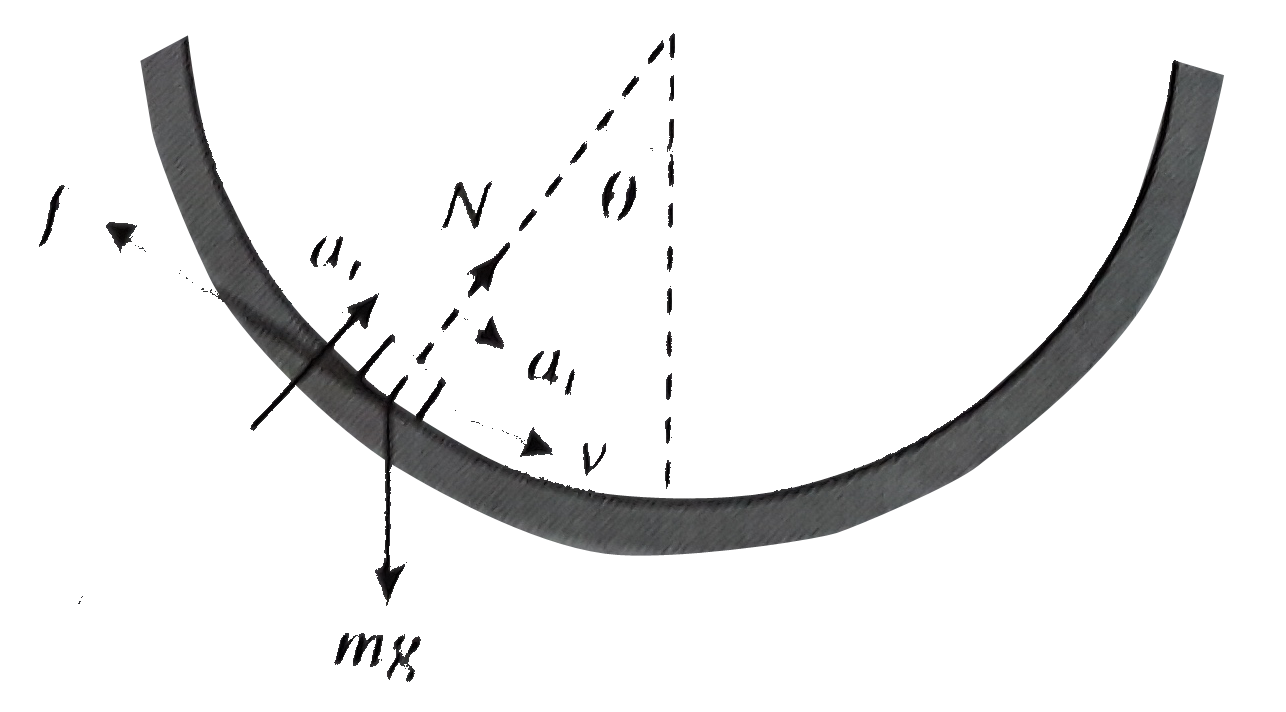
Equation of motion
∑Fr=N−mgcosθ=mar
∑Ft=mgsinθ−fk=ma1
Butfk=μN
And centripetal acceleration is ar=v2R
Substituting fk from Eq (iii) and ar from Eq (iv) , in Eq we get
ar=gsinθ−μNm
Now substituting N from Eq (i) in Eq (v) we get
at=g(sinθ−μcosθ)−μv2R
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Solved Examples
Explore 12 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Exercise 7.1
Explore 25 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
A coin is pushed down tangentially from position θ on a cylindrical surface with a velocity v as shown in Fig. If the coefficient of friction between the coin and surface is μ find the tangential acceleration of the coin

View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View Solution
Knowledge Check
A particle of mass m is pulled along an arbitrary curved surface without acceleration as shown in figure. Coefficient of friction between surface and particle is μ. Then

codes:APQRS3124BPQRS3241CPQRS2134DPQRS4312A block B is pushed momentarily along a horizontal surface with an initial velocity v. If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time
 AvgμBgμvCgvDvg
AvgμBgμvCgvDvgA block B is pushed momentarily along a horizontal surface with an initial velocity v. If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time
 AvgμBgμvCgvDvg
AvgμBgμvCgvDvg
The coefficient of friction between two surface is μ=0.8. The tension in the string as shown in the figure is
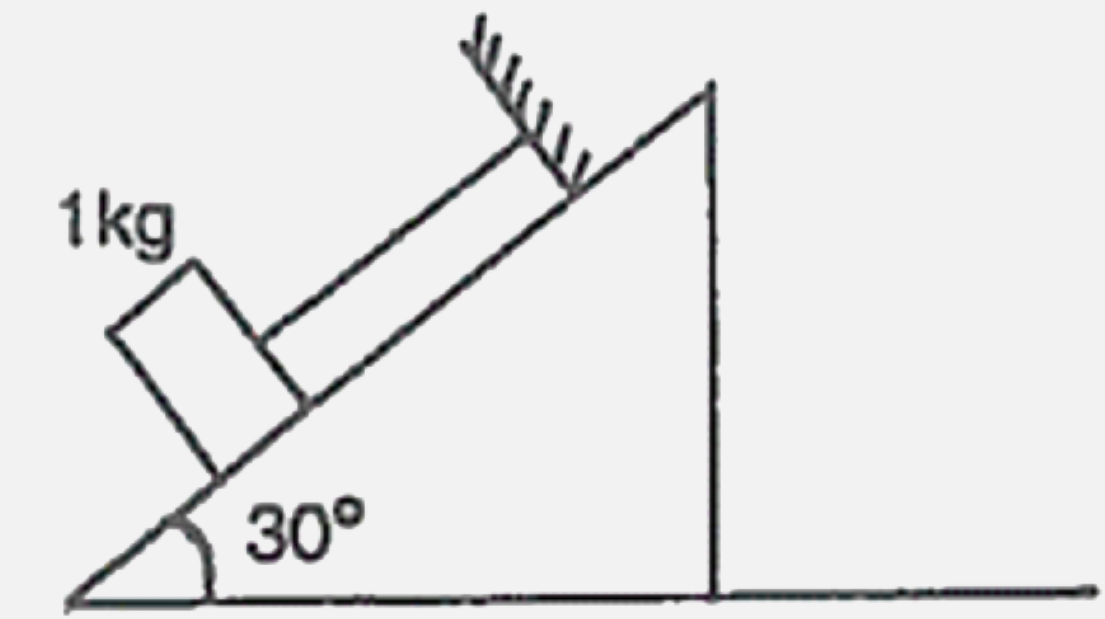
View Solution
For the given dimensions shown in figure, find critical value of coefficient of friction μ
View SolutionA ring of mass M is kept on w horizontal rough surface . A force F is applied tangentially at its rim as shown . The coefficient of friction between the ring and surface is μ Then

View SolutionIf the height of the orbit of a satellite from the earth surface is increased , the tangential velocity of satellite will …………….
View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If mu is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

View Solution

