A turn of radius 20 m is banked for the vehicles going at a speed of 36km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
Angle of banking for designed speed
tanθ=υ20Rg …(i)
V=36kmh−1=10ms−1
⇒tanθ=υ20Rg=10220×10=12
The vehicle may have the tendency to slide up or down depending on the speed of the vehicle .If speed of the vehicle is more it has tendency ti side up and vise- versa
For speed graeter than designed speed : The vehicle has the tendecy to slide . friction will act downward.

In verticle direction ∑Fy=0,Ncosθ−μNsinθ=mg
In horizontal direction ∑Fr=mv2maxR
Nsinθ+μNcosθ=mv2maxR....(i)
Ncosθ−μNsinθ=mg....(iii)
From (ii) and) (iii)
N(sinθ+μcosθ)N(cosθ−μsinθ)=mv2maxRmg⇒(sinθ+μcosθ)cosθ−μsinθ=v2maxRg
⇒(tanθ+μ1−μtanθ)=v2maxRg....(iv)
⇒(tanθ+μ1−μtanθ)=(0.5+0.41−0.4×0.5)=v2max20×10
⇒vmax=15ms−1
For speed less than desigram speed : The vehicle has tendecy to slide down friction will act upward
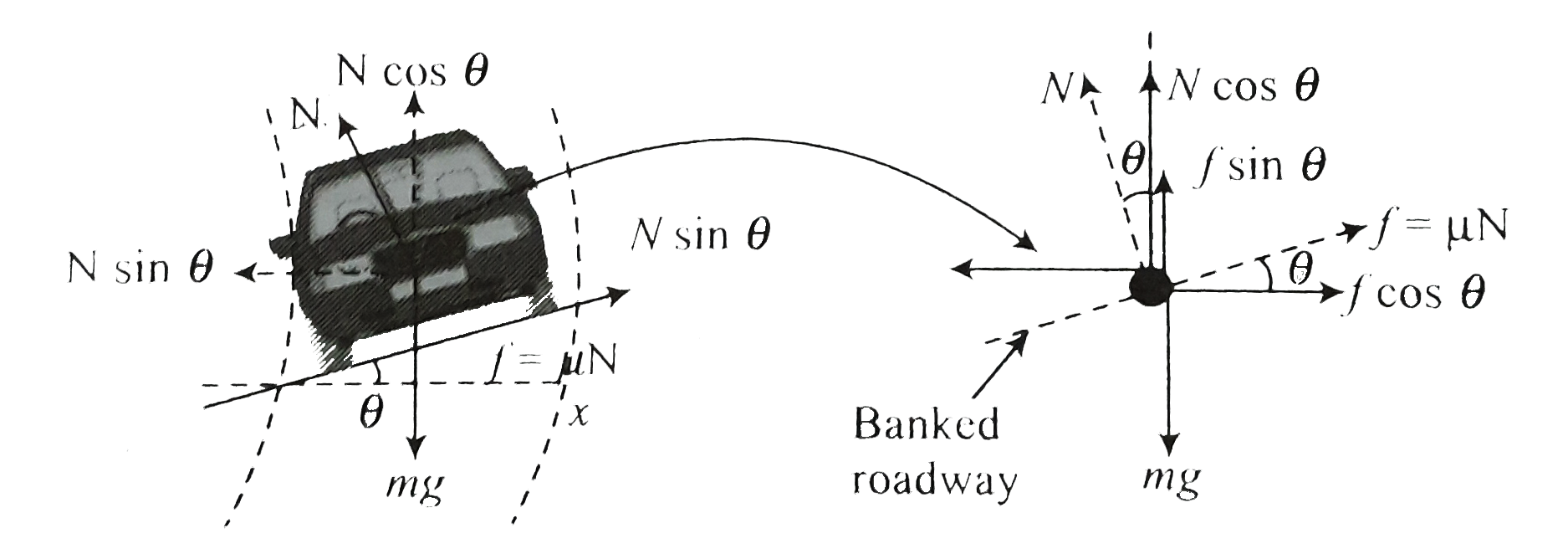
In verticle direction ∑Fy=0,Ncosθ+μNsinθ=mg....(v)
In horizontal direction ∑Fr=mv2maxR
Nsinθ−μNcosθ=mv2maxR....(vi)
From (v) and) (vi) we get(sinθ−μcosθ)cosθ+μsinθ=υ2Rg
(tanθ−μ1+μtanθ)=υ2Rg⇒υmin=10√16ms−1
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.1
25 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A cyclist speeding at 4.5km h−1 on a level road takes a sharp circular turn of radius 3 m without reducing the speed The coefficient of static friction between the road and the tyres is 0.1 will the cyclist slip while taking the turn (i) with a speed of 4.5km h−1 and (ii) with a speed of 9kmk−1?
View SolutionA car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tire and the road is μs=2.0, find the maximum speed the car can take without skidding.
View Solution
Knowledge Check
Consider a car moving along a straight horizontal road with a speed of 72 km/h. If the coefficient of static friction between road and tyres is 0.5, the shortest distance in which the car can be stopped is
A30 mB40 mC72 mD20 mA motorcycle is travelling on a curved track of radius 500 m. If the coefficient of friction between road and tyres is 0.5, the speed avoiding skidding will be
A50 m/sB75 m/sC25 m/sD35 m/sA turn of radius 600 m is banked for a vehicle of mass 200 kg going with a speed of 180kmh−1 . Determine the banking angle of its path.
A22.6∘B19.8∘C30.6∘D40.8∘
A cyclist speeding at 4.5km h−1 on a level road takes a sharp circular turn of radius 3 m without reducing the speed The coefficient of static friction between the road and the tyres is 0.1 will the cyclist slip while taking the turn (i) with a speed of 405km h−1 and (ii) with a speed of 9kmk−1?
View SolutionA circular race track of radius 400 m is banked at an angle of 10∘ . If the coefficient of friction between the wheels of a race car and the road is 0.2 , what is the (i) optimum speed of the race car to aviod wear and tear on its tyres .
maximum permissible speed to aviod slipping ?
View SolutionA cyclist speeding at 4.5 km/h on a level road takes a sharp circular turn of radius 3 m without reducing the speed. The coefficient of static friction between the road and the tyres is 0.1.
(i) Will he slip while taking the turn?
(ii) Will he slip if his speed is 9 km/h?
View SolutionWhat would be the maximum speed of a car on a road turn of radius 30 m, if the coefficient of fraction between the types and the road is 0.4 ?
View SolutionConsider a car moving along a straight horizontal road with a speed of 36 km/h. If the coefficient of static friction between road and tyers is 0.4, the shortest distance in which the car can be stopped is (Take g=10m/s2)
View Solution
