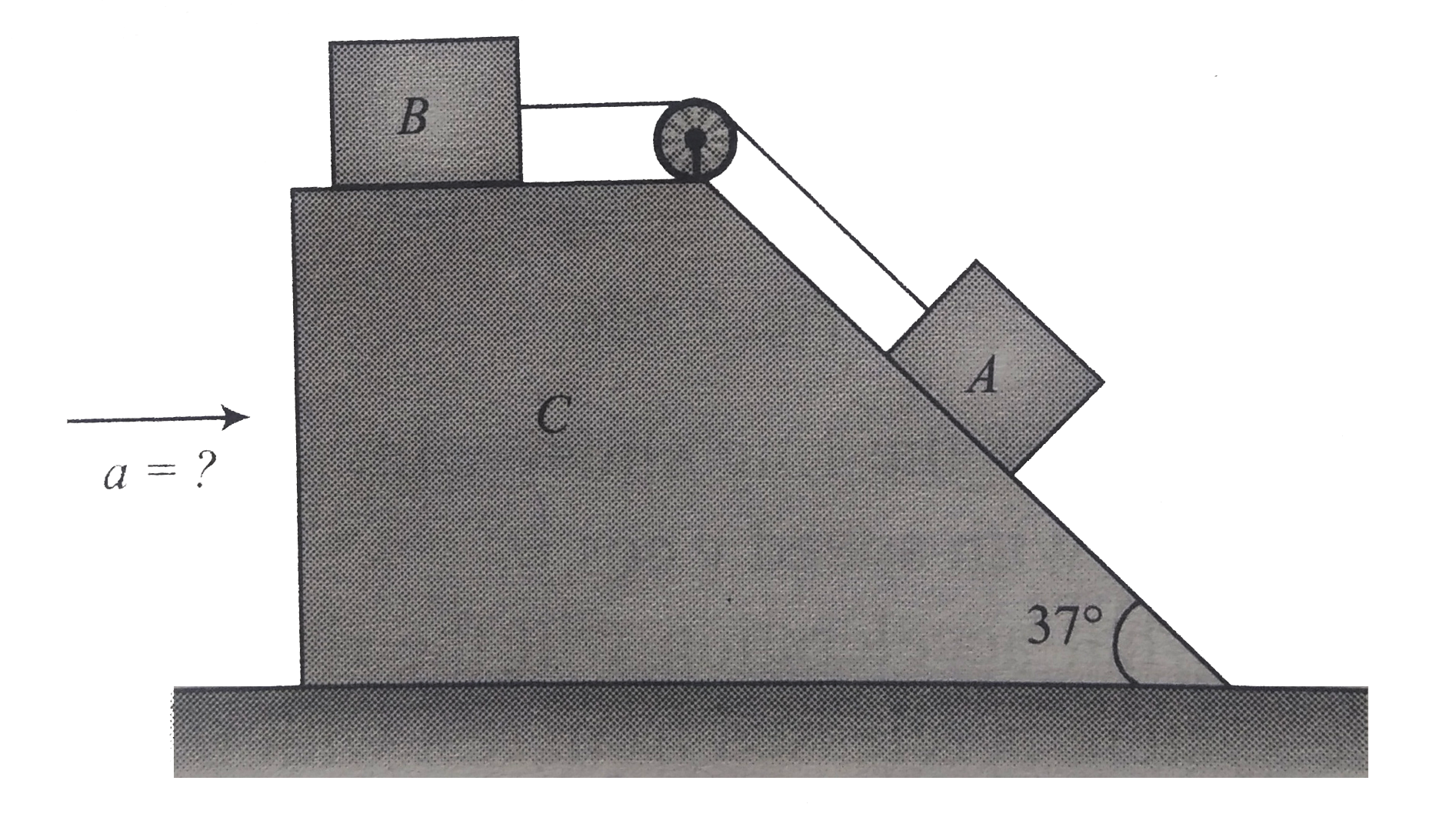
The pulley of the system shown in Fig is massless and frictionless and thread and thread is inextensible Then horizontal surface over which block C is smooth while for all the remaining surface is μ

Calculate minimum acceleration a with which the system should be moved to the right so that suspented block A(mass m ) and B (mass M and M>m)can remain stationary relative to C
Since blocks AandB are stationary relative to C It means their acceleration will also be equal to a (rightward). Since mass m of block A is less than mass M of block B hence block A has tendency to slip upward while B has tendency to slip downward .
Since A has to slip upward therefore on its left surface will act downward and friction on both the surface of block B will act upward because it has tendency to slip downward hence , their free body diagram will be as shown in fig
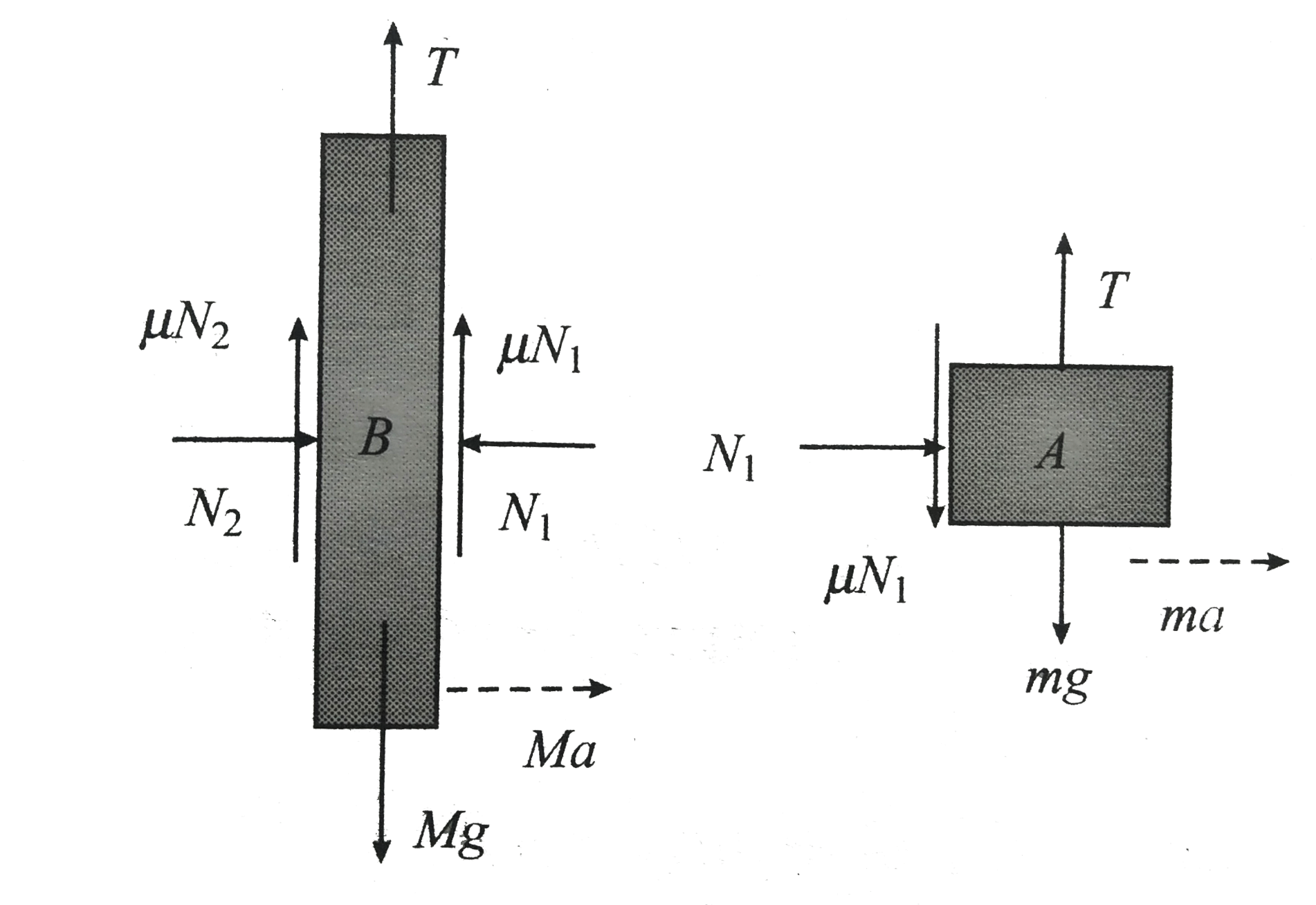
For horizontal forces on A,N1=ma
For verticle equillibruim of A,
T=(μN1+mg)=(μma+mg) ....(i)
For horizontal forces on BN2−N1=Ma
or N2=(m+M)a
For verticle equillibruim of B
T+μN1+μN2=Mg
(μma+mg)+μma+μ(m+M)a=Mg
a=M−mμ(3m+M).g
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.1
25 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
In the arrangement , shown below pulleys are massless and frictionless and threads are inextensible , block of mass m1 will remain at rest if
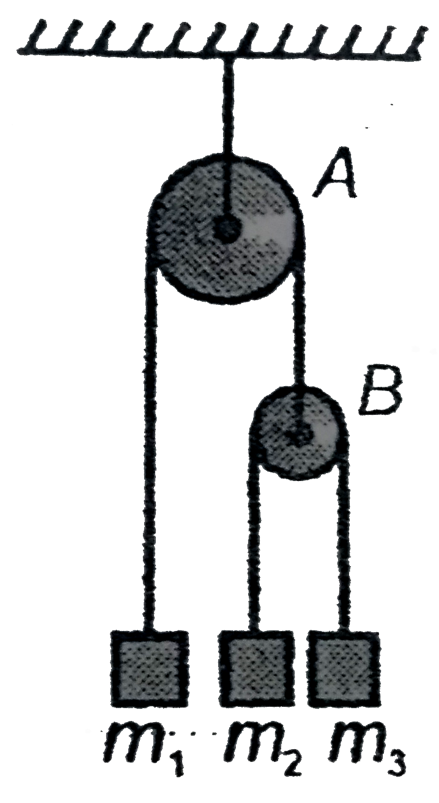
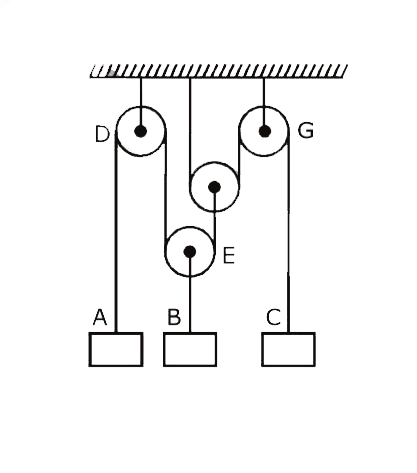
View SolutionPulleys shown in the system are massless and fricionless. Threads are inextensible. The mass of blocks A, B, and C are m1=2kg,m2=4kg, and (m3)=2.75kg, respectively. Calculate the acceleration of each block.

View Solution
Knowledge Check
In the arrangement shown below, pulleys are mass-less and friction-less and threads are in-extensible. Block of mass m1 will remain at rest if :
 A4m1=1m2+1m3Bm1=m2=m3C1m1=1m2+1m3D1m2=2m2+3m1
A4m1=1m2+1m3Bm1=m2=m3C1m1=1m2+1m3D1m2=2m2+3m1In the arrangement shown below pulleys are mass less and frictionless and threads are in responsible block of mass m1 will remain at rest if :
 A4m1=1m2+1m3Bm1=m2=m3C1m1=1m2+1m3D1m3=2m2+3m1
A4m1=1m2+1m3Bm1=m2=m3C1m1=1m2+1m3D1m3=2m2+3m1Two masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
Agm/MB2gM/mCgm/2MDg(M2−m2)/2M
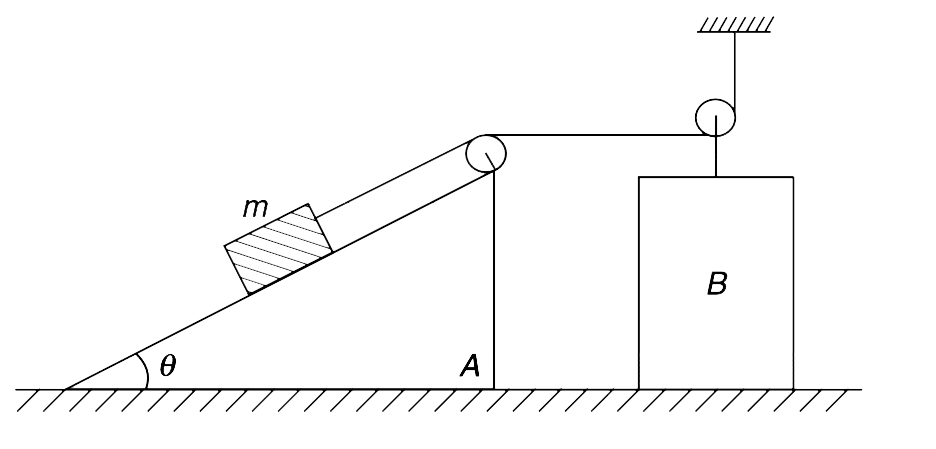
The upper surface of blokc C is horizontal and its right part is inclined to the horizontal at angle 37∘. The mass of blocks A and B are m1=1.4kgandm2=5.5kg, respectively. Neglect friction and mass of the pulley. Calculate acceleration a with which block C should be moved to the right so that A and B can remain stationary relative to it.
View SolutionPulleys shown in the system of the figure are massless and friction less. Threads are inextensible. Mass of block A, B and C are m1kg,m2=4kg and m3=2.75kg, respectively .Calculate acceleration of A block
View SolutionIn the system shown in the figure all surfaces are smooth and both the pulleys are mass less. Block on the incline surface of wedge A has mass m. Mass of A and B are M = 4 m and M0=2 m respectively. Find the acceleration of wedge A when the system is released from rest.
View Solution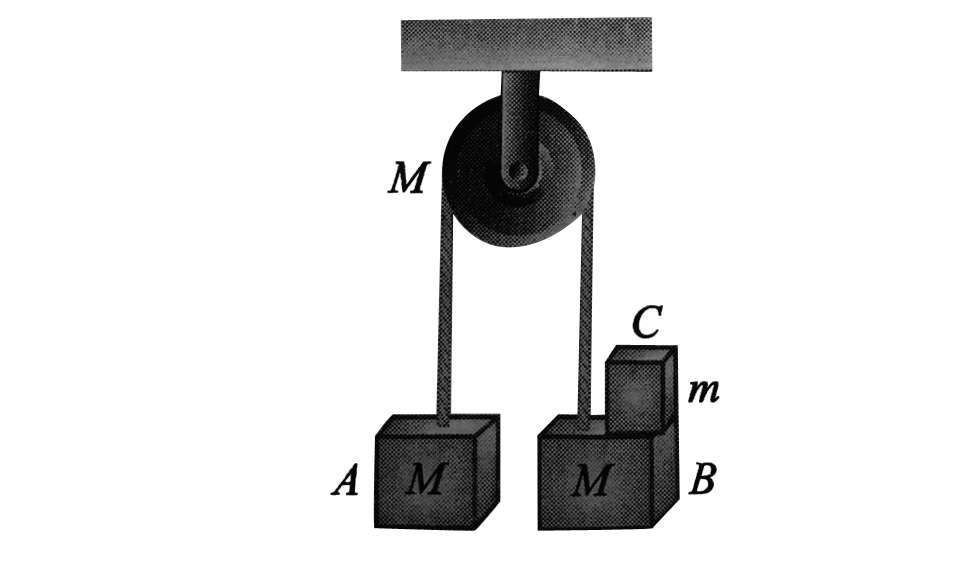
For the following system shown assume that pulley is frictionless, string is massless (m remains on M),
Q. The acceleration of the block A is
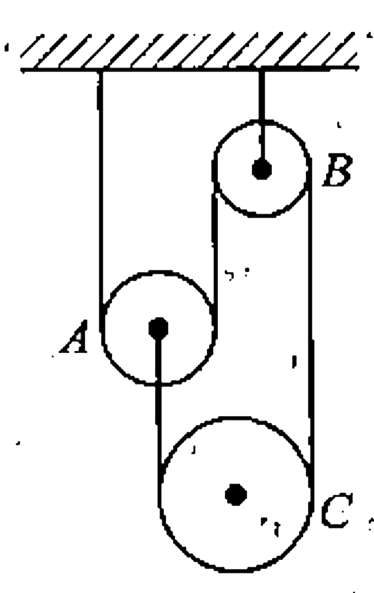
View SolutionIn the arrangement shown in figure-2.124 pulley A and B are massless and the thread is inextensible. Mass of pulley C is equal to m. If friction in all the pulleys negligible, then :
View Solution
