Two block A and B of masses 1kg and2kg respectively are connected by a string, passing over a light frictionless pulley as shown. Another string connect the center of pulley. Both the blocks are resting on a horizontal floor and the pulley is help such that string remains just taut. At moment t=0, a force F=20t starts acting on the pully along vertically upwards direction as shown in figure.Calculate

(a) velocity of A when B loses contact with the floor.
(b) height raised by the pulley upto that instant.
(Take =g=10m/s2)
5ms−1
5/4ms−1
4ms−1
7/3ms−1
The correct Answer is:A
T3=20t,T1=T2=10t
For A to lose contact: 10t=1g⇒1s
For B to lose contact: 10t=2g⇒2s
For C to lose contact: 20t=3g⇒1.5s
aA=T1−1g1 velocity of A when B loses contact.
V1=∫21aAdt=∫21(10t−g)dt=5ms−1
At t=2s,aB=0,aA=10×2×−101=10ms−2
aA/B=aA−aB=10−0=10ms−2.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Assertion-reasoning
Explore 15 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
Two block A and B of masses 1kg and2kg respectively are connected by a string, passing over a light frictionless pulley B as shown. Another string connect the center of pulley. Both the blocks are resting on a horizontal floor and the pulley is help such that string remains just taut. At moment t=0, a force F=20t starts acting on the pully along vertically upwards direction as shown in figure.Calculate

(a) velicity of A when B loses contact with the floor.
(b) height raised by the pulley upto that instant.
(Take =g=10m/s2)
View SolutionTwo blocks A and B having masses m1=1kgm2=4kg are arranged as shown in the figure The pulleys P and Q are light and frictionless. All the blocks are resting on a horizontal floor and the pulleys are held such that strings remains just taut. At moment t=0 a force F=30 t (N) starts acting on the pulley P along vertically upward direction as shown in the figure The time when the blocks A and B loose contact with ground is 4/x sec then x is:
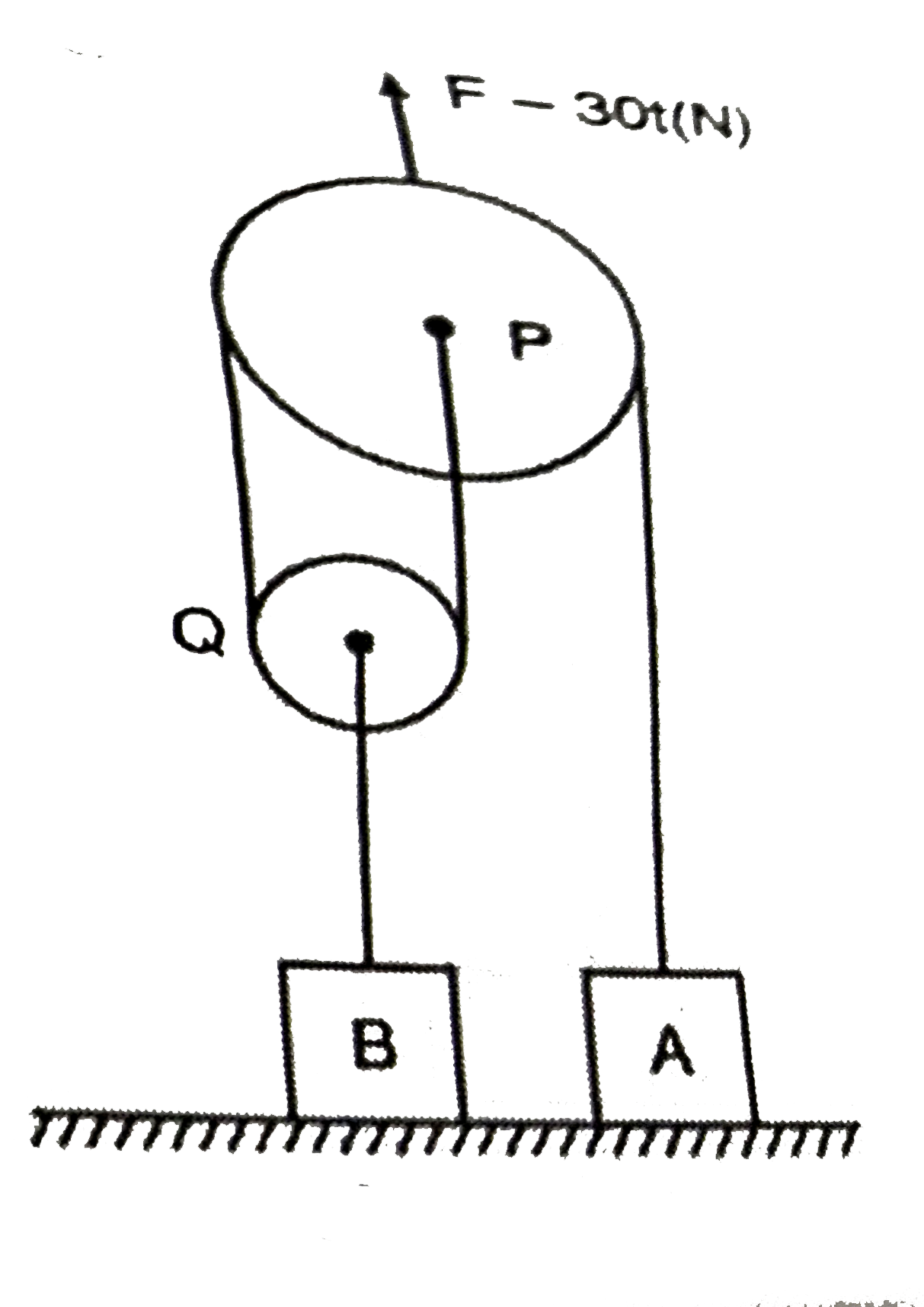
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A188 NB2=368 NC288 ND168 N
A188 NB2=368 NC288 ND168 NTwo masses of 8kg and 4kg are connected by a string as shown in figure over a frictionless pulley.The acceleration of the system is
 A4m/s2B2m/s2CzeroD9.8m/s2
A4m/s2B2m/s2CzeroD9.8m/s2
Two bodies of masses 4kg and 3kg respectively are connected by a light string passing over a smooth frictionless pulley Calculate the acceleration of the masses and tension in the string .
View SolutionTwo block a and B having masses m1=1kg,m2=4kg are arranged as shown in the figure. The pulleys P and Q are light, and frictionless. All the blocks are resting on. a horizontal floor and the pulleys ate held such that strings remains just taut.
At.moment t=0a force F=30t(N) starts acting on thei ipulley p along . vertically upward direction as shown in the pulley P along vertically upward direction as shown in the figure. Calculate.
(i) the time when the blocks A and B loose contact with ground.
(ii) the. velocity of A when B looses contact with ground.
(iii) the height raised. by A upto this instant.
(iv) the work done by the force F upto this instan.
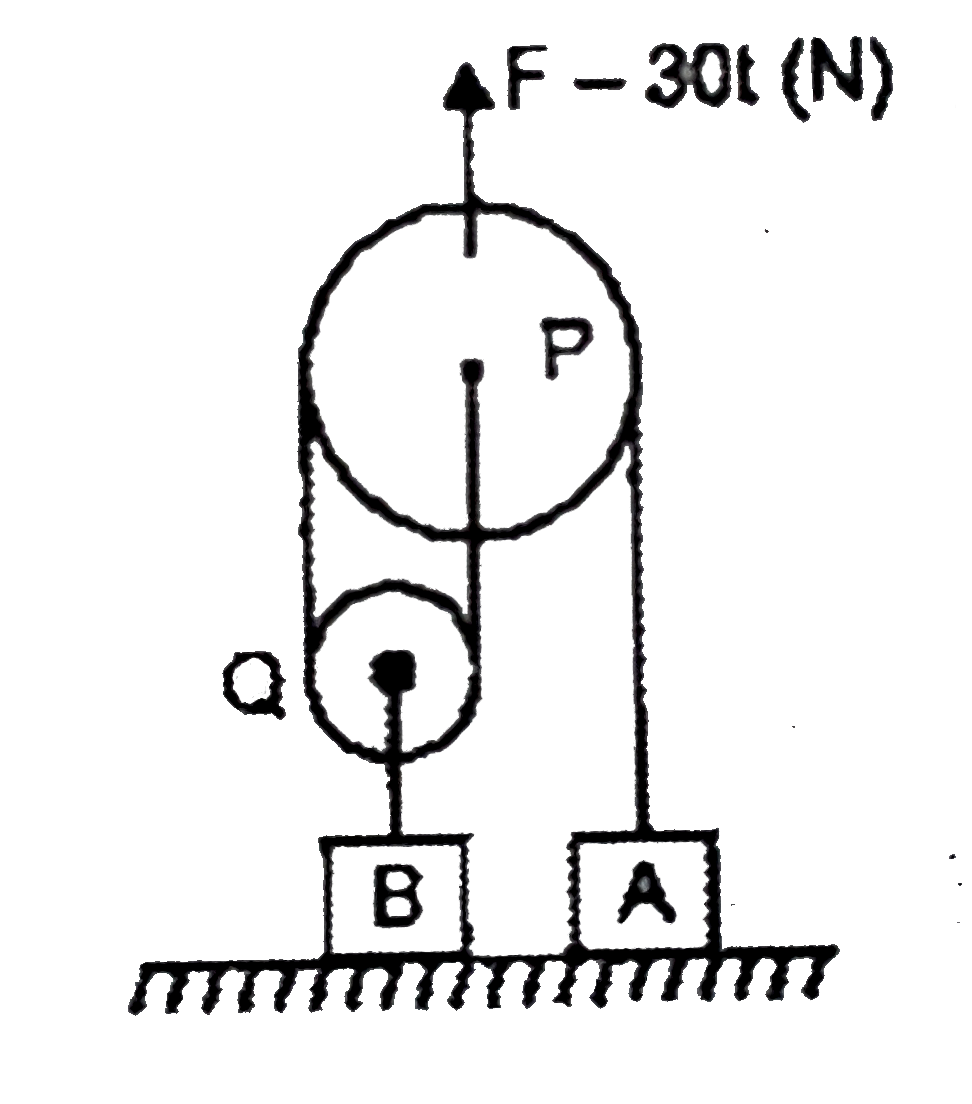
View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is

View SolutionTwo masses of 8 kg and 4 kg are connected by a string as shown in figure over a frictionless pulley. The acceleration of the system is

View Solution

