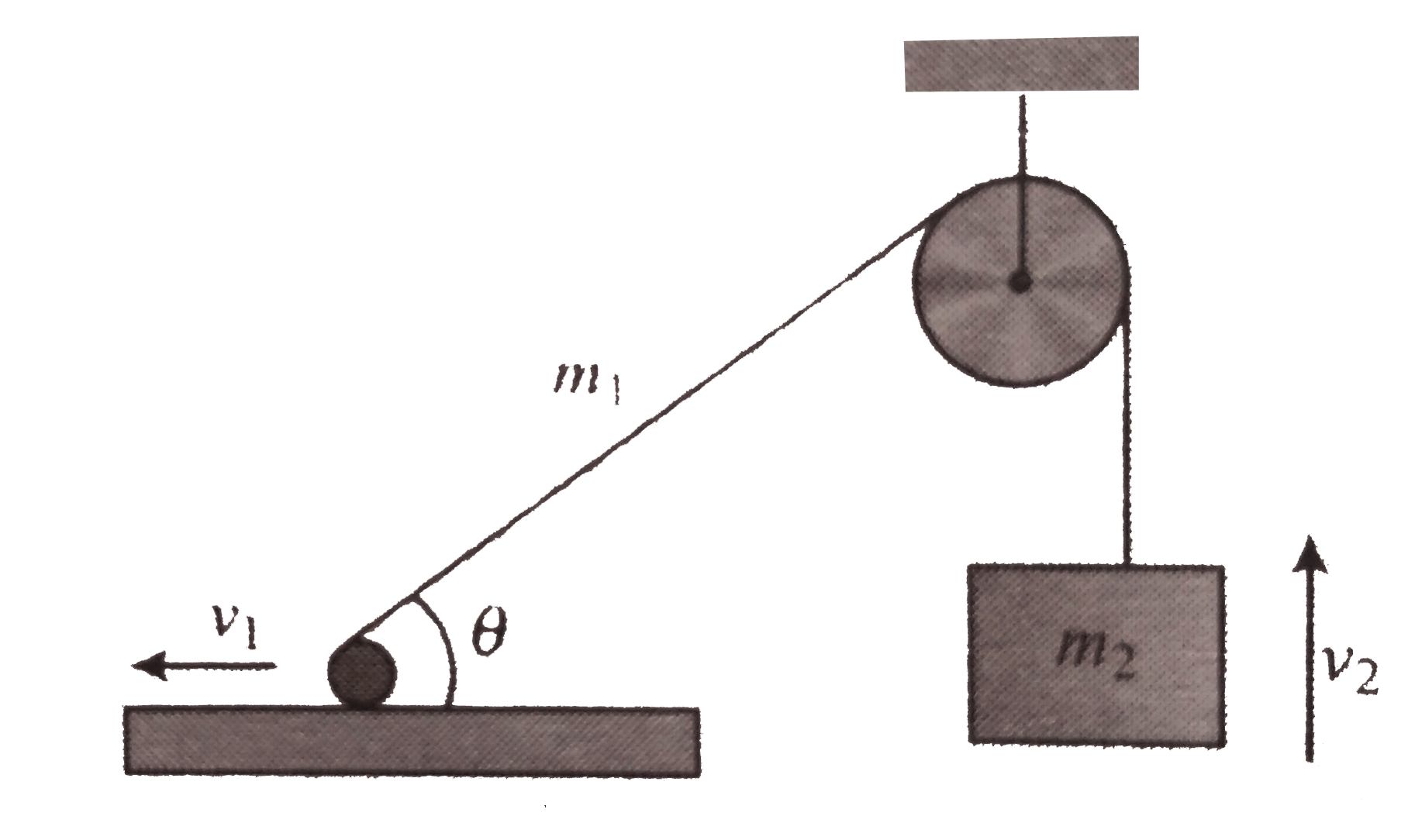
The ring M1 and block M2 are held in the position shown in fig. Now the system is released. If M1>M2, find V1/V2 wheb the ring m1 slides down along the smooth fixed vertical rod by the distance h.
To solve the problem, we need to analyze the motion of the ring M1 and the block M2 when the system is released. Here’s a step-by-step solution:
Step 1: Understand the System
The system consists of a ring M1 sliding down a smooth vertical rod and a block M2 hanging from a pulley. When M1 slides down by a distance h, M2 will move upward.
Step 2: Establish the Relationship Between Distances
When the ring M1 moves down by a distance h, the block M2 will move up by a distance h as well. However, due to the pulley system, the relationship between the distances moved by M1 and M2 is not direct.
Let’s denote:
- V1 = velocity of M1
- V2 = velocity of M2
Step 3: Use Conservation of Energy
Since there are no non-conservative forces doing work (the rod is smooth), we can apply the conservation of energy principle. The potential energy lost by M1 will equal the potential energy gained by M2.
The potential energy lost by M1 when it descends a height h is:
PElost=M1gh
The potential energy gained by M2 when it rises a height h is:
PEgained=M2gh
Step 4: Set Up the Energy Equation
Setting the potential energy lost equal to the potential energy gained gives us:
M1gh=M2gh
Step 5: Analyze Velocities
From the geometry of the system, we can establish a relationship between the velocities. When M1 moves down by h, M2 moves up by h as well, but due to the pulley, the relationship between their velocities can be expressed as:
V1=2V2
Step 6: Find the Ratio of Velocities
To find the ratio V1V2:
V1V2=2
Final Answer
Thus, the ratio of the velocities when the ring M1 slides down by a distance h is:
V1V2=2
---
The system consists of a ring M1 sliding down a smooth vertical rod and a block M2 hanging from a pulley. When M1 slides down by a distance h, M2 will move upward.
When the ring M1 moves down by a distance h, the block M2 will move up by a distance h as well. However, due to the pulley system, the relationship between the distances moved by M1 and M2 is not direct.
- V1 = velocity of M1
- V2 = velocity of M2
Since there are no non-conservative forces doing work (the rod is smooth), we can apply the conservation of energy principle. The potential energy lost by M1 will equal the potential energy gained by M2.
PElost=M1gh
PEgained=M2gh
Setting the potential energy lost equal to the potential energy gained gives us:
M1gh=M2gh
From the geometry of the system, we can establish a relationship between the velocities. When M1 moves down by h, M2 moves up by h as well, but due to the pulley, the relationship between their velocities can be expressed as:
V1=2V2
To find the ratio V1V2:
V1V2=2
Thus, the ratio of the velocities when the ring M1 slides down by a distance h is:
V1V2=2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
Knowledge Check
Two blocks of masses m1 and m2 are kept on a smooth horizontal table as shown in figure. Block of mass m1 (but not m2 is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass m1 after the system is released is
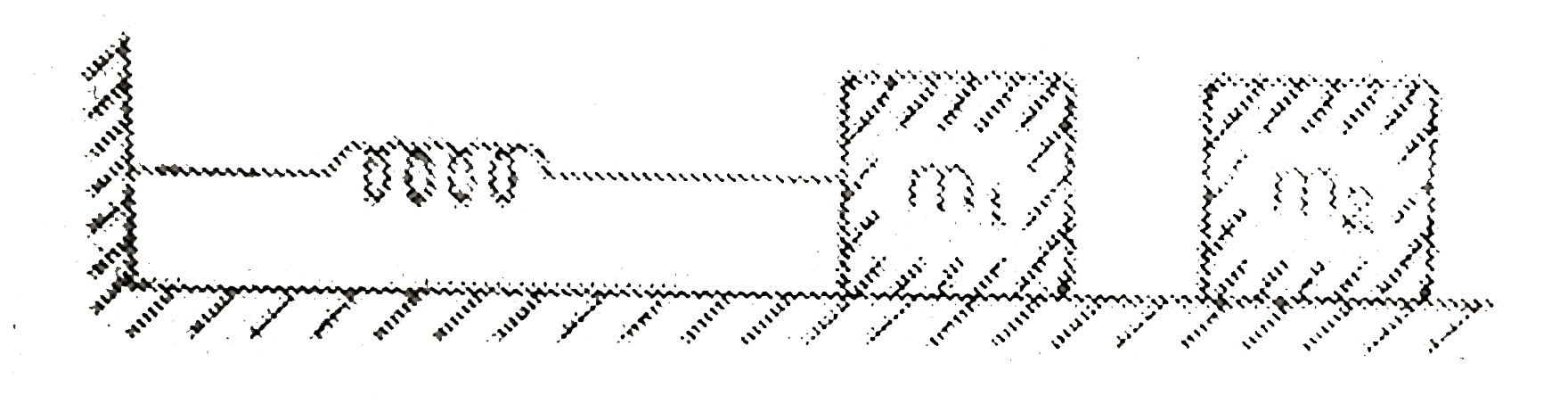 Ad√m1m1+m2Bd√m2m1+m2Cd√2m2m1+m2Dd√(2m1m1+m2
Ad√m1m1+m2Bd√m2m1+m2Cd√2m2m1+m2Dd√(2m1m1+m2Two blocks of masses M1=4 kg and M2=6kg are connected by a string of negligible mass passing over a frictionless pulley as shown in the figure below. The coefficient of friction between the block M1 and the horizontal surface is 0.4. when the system is released, the masses M1 and M2 start accelrating. What additional mass m should be placed over M1 so that the masses (M1+m) slide with a uniform speed?
 A12 kgB11 kgC10 kgDkg
A12 kgB11 kgC10 kgDkgFor the system shown in fig, there is no friction anywhere. Masses m1andm2 can move up or down in the slots cut in mass M. Two non-zero horizontal force F1 and F2 are applied as shown. The pulleys are massles and frictionless. Given m1≠m2

Let F1 and F2 are applied in such a way that m1andm2 do not move w.r.t. M. then what is the magnitude of the acceleration of M? Let m1>m2.A(m1+m2)gM+m1+m2B(m1−m2)gMC(m1−m2)gM+m1+m2DF1−F2M
Use of dilution formula (M1V1=M2V2)

View SolutionIn fig. a ball of mass m1 and a block of mass m2 are joined together with an inextensible string. The ball can slide on a smooth horizontal surface. If v1 and v2 are the respective speeds of the ball and the block, then determine the constraint relation between the two.
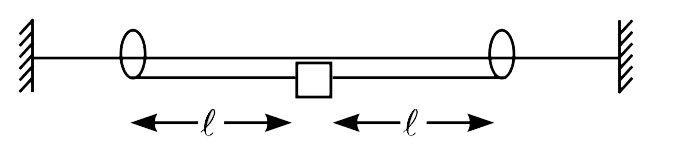
View SolutionTwo small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@)withvertical.(Takeg = 10 m//s^2)
View SolutionTwo masses m1 and m2(m1<m2) are positioned as shown in figure,m1 being on the ground and m2 at a height h above the ground.When m2 is released, the speed at which it hits the ground will be
View SolutionConsider a system of masses M1 and M2(M1>M2) connected by a massless string in fig the system is pulled by a force F from the side of mass M1 and in fig
(b) the system is pulled by the same force F from the side of mass M2 then:

View Solution

 .
.