What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes and angle θ2 with the horizontal?
u2cos2sec3(θ2)g
u2cos2sec3(θ2)2g
2u2cos2θsec3(θ2)g
u2cos2θsec3(θ2)√3g
The correct Answer is:A
(a) We know that ac=v2r⇒r=v2ac, where r is known as radius of curvature. At the highest point, v=ucosθ,
ac=g⇒r=u2cos2θg
Similarly, find the velocity and ac at the given point and then find r.ac will be component of g perpendicular to velocity at that point (Fig. S5.93).
vcos(θ/2)=ucosθ
⇒v=ucosθsec(θ/2)
ac=gcos(θ/2)
Now find r=v2ac
h=H/2,vcosϕ=ucosθ ...(i)
v2sin2ϕ=u2sin2θ−2g(H)2...(ii)
Squaring Eq. (i) and adding in Eq. (ii), we get
v2=u2−gH where H=u2sinθ2g
ac=gcosϕ=gucosθv
Now r=v2ac.
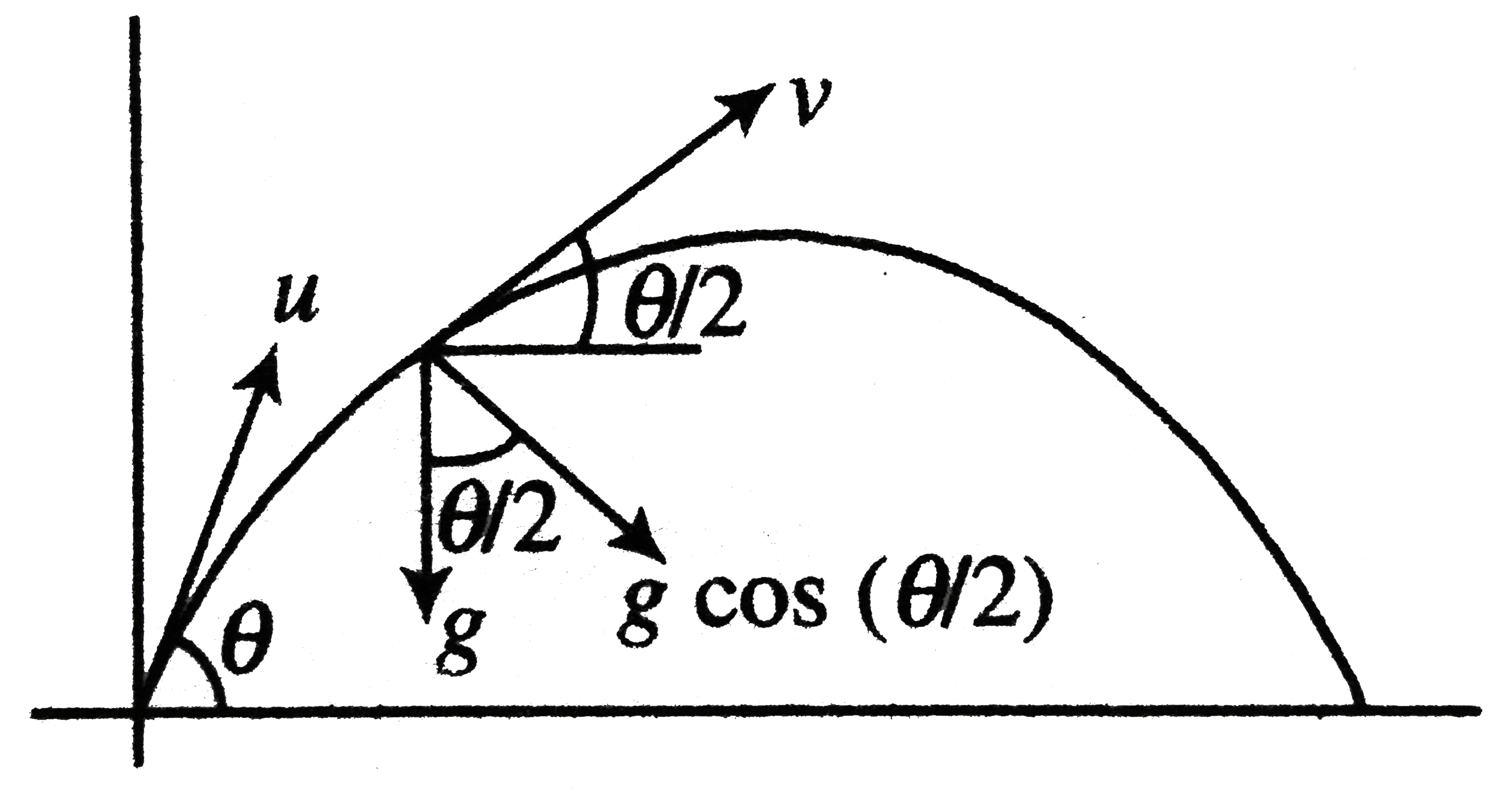 ,
,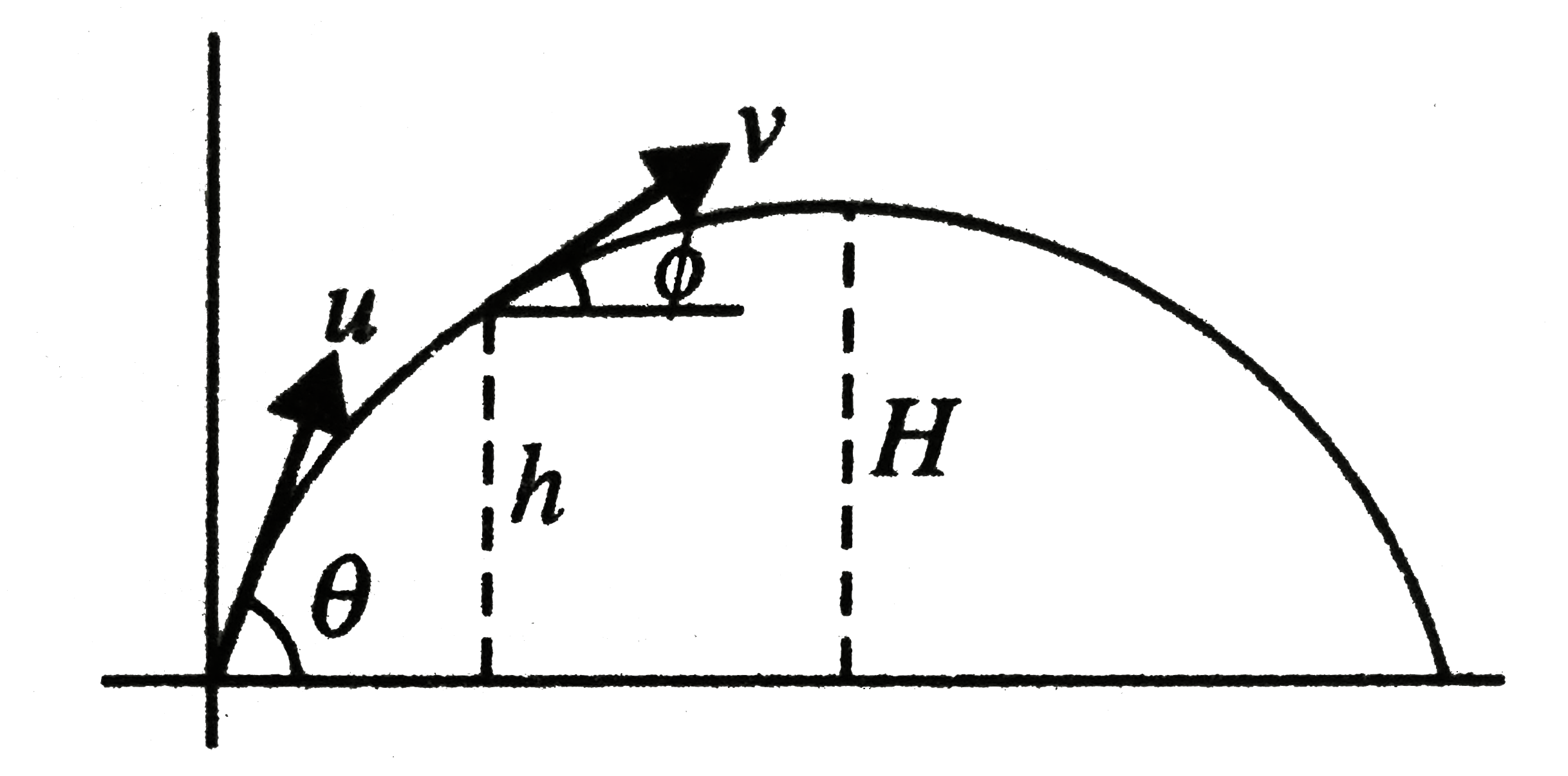 .
.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Assertion - Reasoning
Explore 5 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A particle is projected with a speed u at an angle 60∘ with the horizontal.What is the radius of curvature of the parabola traced out by the projectile at a point where the particle velocity makes an angle 30∘ with the horizontal?
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle θ with the horizontal, at a point where the velocity of particle makes an angle θ/2 with the horizontal.
View Solution
Knowledge Check
A particle is fired from a point on the ground with speed u making an angle θ with the horizontal.Then
Athe radius of curvature of the projectile at the highest point is u2cos2θgBthe radius of curvature of the projectile at the highest point is u2sin2θgCat the point of projection magnitude of tangential acceleration is gsinθDat the point of projection magnitude of tangential acceleration is gcosθA particle is executing vertical SHM about the highest point of a projectile. When the particle is at the mean position, the projectile is fired from the ground with velocity u at an angle θ with the horizontal.The projectile hits the oscillating particle .Then, the possible time period of the particle is
AusinθgB2usinθgC2usinθ3gDall the aboveA particle is projected with initial speed u at an angle θ above the horizontal . Let A be the point of projection , B the point where velocity makes an angle θ/2 above the horizontal and C the highest point of the trajectory .
Radius of curvature of the trajectory at point C isAu2cos3θg2B2u2cos2θgCu2cos2θgDu2cos3θg
For a projectile first with velocity u at an angle θ with the horizontal.

View SolutionWhat is the radius of curvature of the parabola traced out by the projectile.Projected with a speed u=√30 at angle θ=60∘ with the horizontal at a point where the particle velocity makes an angle θ/2 with the horizontal ?
View SolutionA projectile is fired with a velocity 'u' making an angle θ with the horizontal. Show that its trajectory is a parabola.
View SolutionA particle is projected with initial speed u at an angle θ above the horizontal . Let A be the point of projection , B the point where velocity makes an angle θ/2 above the horizontal and C the highest point of the trajectory .
Radius of curvature of the trajectory at point B is
View SolutionA particle is projected with initial speed u at an angle θ above the horizontal . Let A be the point of projection , B the point where velocity makes an angle θ/2 above the horizontal and C the highest point of the trajectory .
Radius of curvature of the trajectory at point A is
View Solution

